CycleGAN Paper Summary
CycleGAN
Preface
GAN常用作风格迁移或者是object transfiguration,但是普通的GAN实际上并不能很好地胜任这些任务。原始的GAN是从一个隐含向量z(常服从一个简单的多维分布)映射到一个具有丰富信息的更高维空间的过程,而这种映射往往“arbitrary”,它可以乱射(随机性的生成)。比如在object transfiguration中,A->B集合映射过程可以通过此网络实现,但B集合进入网络后,生成出来的(例应是原始的B)却与原始B相差很远。当然,在object transfiguration中,更加有挑战性的问题是,对于pix2pix论文提出的成对图像转换而言,成对图像一般很难获得。如果只有两个集合A / B,A / B内的对象为不同属性的,那么在没有预先产生匹配关系的情况如何将A / B集合内的物体互相映射呢?
在论文 Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks (arXiv链接:【arXiv Preview】🔗)中,作者提出了:Cycle Consistancy的思想(好了,xxx一致性,听多了)(循环一致性),在误差函数中添加了两项:
- 循环一致误差(CCL),用于控制一致性(显然)
- 本征一致性,感觉作者没有提。但是我觉得可以通过CCL推导出来。
复现的结果
由于受到设备的限制(GeForce MX150,三年的i5小米Air轻薄本的渣显卡)网络只训练了25个迭代(原文使用了50个学习率恒定迭代,此后50个迭代学习率线性递减至0),也没有修改学习率设置。一张图片大概需要计算1s,995张图片需要15min+才能完成一轮迭代。结果如图:
两行为一组,一共六行。前两行是橙子->苹果,中间两行是苹果->橙子,后两行是初始情况(欠训练时的结果)。
论文的细节
CCL的定义
在【3. Formulation】中,作者提到:循环一致性就是:假设集合\(X\)与\(Y\)分别包含两种类型物体,\(G\)与\(F\)分别是两个生成器,其中\(G\)用于利用集合\(X\)对象生成集合\(Y\)的对象,\(F\)则正好相反。也就是: \[ G: X\rightarrow Y,G(x)\rightarrow Y,\text{for each }x\in X \\ F: Y\rightarrow X,F(y)\rightarrow X,\text{for each }y\in Y \] 那么对于这样的映射,应该有:\(F(G(x))\approx x\)(也就是经过两个生成网络后,\(X\rightarrow Y\rightarrow X\)),数据应该和初始输入保持一致。在object transfiguration或是style transfer中,我觉得这种想法十分自然,并且很妙。由于在这两个问题中,图像本身的形状特征并不会发生巨大的变化,变化的只是颜色 / 纹理属性,在object transfiguration中,从物体A变成物体B以及其反过程是对称的,风格迁移中,风格的加入和消除也是对称的(可以将原图看成另一种风格),那么由反函数的性质,应该存在上式的结果。于是,作者定义了一个Cycle Consistancy Loss: \[ L_{cyc}(G,F,x,y)=\Vert G(F(y))-y\Vert_1+\Vert F(G(x))-x\Vert_1 \] 也就是用(理论上的identity变换)变换前后的图像的1-范数进行比较。显然是越小越好,希望这种identity映射前后基本不变。
但其实整篇论文传达的意思就那么简单,18页的论文,放了一半页数的图,但是做的事情却牛大了(虽然已经是4年前的论文了)。不得不吐槽一下,原论文中提到的信息不太多(可能是因为这些基本的问题作者认为大家都应该明白所以不说了?),所以这篇文章非常好懂,复现起来也相对简单(但是我太菜了,遇到了一些坑)。
CCL可以推出什么
个人认为,既然存在CCL(\(X\rightarrow Y\rightarrow X\)循环映射不变),那么以下想法也是自然应该成立的:设\(x\in X, y \in Y\),那么应该存在: \[ \begin{equation} G:X\rightarrow Y, G(y)\approx y\\ F:Y\rightarrow X, F(x)\approx x \end{equation} \] 也就是说,由于G的输出空间为\(Y\)(期望),所以对于已经在y空间里的数据而言,生成网络不应该改变其特征。所以可以定义本征一致性loss: \[ \begin{equation}\label{equ:ind} L_{ind}=\mathbb E_{p\_data(y)} \Vert G(y)-y\Vert_1 + \mathbb E_{p\_data(y)} \Vert F(x)-x\Vert_1 \end{equation} \] 可以认为这是循环的一半情况吧,但是确实是应该加入到loss项中的,既然存在循环一致性,那么本征一致性理论上来说也是存在的。
于是,full objective应该是: \[ \begin{equation} L_{full}(X,Y,G,F)=L_{adv}(X,Y,G,F)+L_{cyc}(X,Y,G,F)+L_{ind}(X,Y,G,F) \end{equation} \]
网络结构
生成器
论文中的生成器采用了ResNet结构,首先图片都是256 * 256 * 3的图片,以6个Residual Block结构进行说明:
- 输入层:输入3 输出64,\(7\times 7\)
大小的卷积网络,使用ReLU激活函数,InstanceNorm
- Reflection Padding
- 输入64 输出128,\(3\times 3\)
卷积网络,步长2,其余同上
- Reflection Padding
- 输入128 输出256,\(3\times 3\) 卷积网络,步长2,其余同上
- Residual Block 1,256->256,\(3\times 3\) 卷积网络,步长2,其余同上,个人使用了ZeroPadding
- Residual Block 2,Residual Block 3,Residual Block 4,Residual Block 5,Residual Block 6
- 非整数步长的卷积(ConvTranspose,反卷操作), \(3\times 3\) ,步长1/2,256->128
- 非整数步长的卷积, \(3\times 3\) ,步长1/2,128->64
- 输出层,(64->3)其余同输入层,Tanh激活
判别器
判别器使用PatchGAN结构,也就是说不只输出一个值(比如过卷积后再过全连接输出1)。输出的是一个super image,super image是一张size更小的单通道图,每个像素表示的是:判别器输出的结果,图像上每小块为real的概率(重新组织的特征图)。也就是说,输出层只需要卷积,输出卷积结果。
- \(4\times 4\)
Convolution,64->128,很奇怪吧。偶数大小的kernel,所以anchor在哪?
LeakyReLU(0.2)
- InstanceNorm
- \(4\times 4\) Convolution,128->256 LeakyReLU(0.2)
- \(4\times 4\) Convolution,256->512 LeakyReLU(0.2)
- \(4\times 4\) Convolution,512->1,直接输出
额,不讲武德。为什么网络结构细节放在Appendix?搞得我以为我读完了,最后一乱翻发现了更重要的东西。
原始GAN模式崩塌?
模式崩塌的定义
模式崩塌也就是多个输入映射到同一个输出上的情况。这通常出现在输出模式具有多峰分布的情况。通常我们希望,在目标分布(不可知,但是可以通过采样学习近似)多峰的情况下,拟合的近似分布也应该是多峰的。但如果出现了生成器过强的情况,直接导致生成器每次都拟合到其中一个峰上,就很可能导致模式崩塌。
上图说明的是,多峰分布时,每一次训练生成器后的生成分布。训练造成了模式崩塌,也就是输出的低丰富性,这就失去了GAN本身的意义。
Goodfellow在论文中提到两种可能产生模式崩塌的原因:
JS/KL散度的使用导致模式崩塌
JS散度: \[ \begin{equation}\label{equ:js} 2D_{JS}(P_R|P_G)=\int_xP_R(x)log(\frac{P_R(x)}{\frac{P_R(x) + P_G(x)}{2}})dx + \int_xP_G(x) log(\frac{P_G(x)}{\frac{P_R(x) + P_G(x)}{2}})dx \end{equation} \] KL散度: \[ \begin{equation} D_{KL}(P|Q)=\int_xP(x)log(\frac{P(x)}{Q(x)})dx \end{equation} \] KL散度能造成更加恐怖的模式崩塌。由于KL散度的非对称性,每次求导都会往特定方向逼近。求导时往特定方向趋近的问题导致了模式崩塌?为什么会这样?KL散度的不对称性决定了其可以从两个方向进行观察,两个方向上的KL散度不是相同的,Goodfellow称\(D_{KL}(p_{data}\Vert p_{model})\)(以data分布为主导的KL散度)为正KL散度,\(D_{KL}(p_{model}\Vert p_{data})\)为逆KL散度。正KL散度和逆KL散度在优化上的表现是有所不同的。可以从直观上理解,前者是给定数据分布(的计算 / 估计)时,模型分布于数据分布的差别,那么此时模型分布 将会是被动的,只要能达到最小拟合的情况,模型分布怎么样都可以。
如上图左图,由于原始(数据)分布已知,模型分布为了产生最小散度,形状可以很奇怪。而在逆KL散度中,已经知道的是模型分布,也就是说:已经出现在模型中的模式概率分布大,尚未出现的模式概率分布小。这样一加权,就会让已经生成的模式被强化,造成单峰性(如上图右)。
这两种KL散度倾向性不同:
- 正KL散度倾向于满足数据分布,不考虑模型已经有的分布,所以很可能生成一些奇怪的模式(比如上图中概率分布大的部分在两峰中间,这是不合理的),但是理论上其多样性更佳
- 逆KL散度倾向于生成已经存在的模式,不习惯于跳出圈子。显然这样做会产生更多我们熟悉的模式,更少奇怪的新模式,但是容易引起模式崩塌。
关于这点,Goodfellow这样说到:
We can think of \(D_{KL}(p_{data}\Vert p_{model})\) as preferring to place high probability everywhere that the
data occurs, and \(D_{KL}(p_{model}\Vert p_{data})\) as preferrring to place low probability wherever the data does not occur.
min/max顺序问题
Goodfellow在GAN论文中也提到,GAN的原理(min max)可能会引起模式崩塌。通常我们说,GAN是:minmax结构的,也就是: \[ \begin{equation}\label{equ:minmax} G^*=\mathop{argmin}_{G} \mathop{max}_{D}L(G,D) \end{equation} \] 其意义也就是(在前某篇文章中提到过):在判别器最优的情况下进行生成器的最优化。我们希望在一个十分强的判别器存在的情况下仍然能尽可能优化生成器,直到生成器骗过判别器。而Goodfellow说到:
We use it in the hope that it will behave like min max but it often behaves like max min.
max min也就是公式\(\eqref{equ:minmax}\)对于min / max的取反结果。个人认为可以这样理解:max min结构也就是:训练生成器在内循环,训练判别器在外循环。直观上看也就是每一次训练判别器,可能会训练多次生成器。这样是不好的。判别器训练一次之后,生成器会有过拟合到判别器认为最像real data的一种(或少数几种)模式上的趋势(由于生成器要训练多次)。这就导致了模式崩塌。关于这个理解,原文是这样写的:
The generator is thus asked to map every z value to the single x coordinate that the discriminator believes is most likely to be real rather than fake.
有些情况下可能会导致GAN的行为更像max min而非min max。个人认为:训练一次判别器后训练多次分类器可能造成此情况(我之前也这么写过,效果是好的,毕竟生成出来的图片最像真的,但是多样性变差了)。
复现的细节
反卷积过程
在CycleGAN[网络结构细节]中,作者使用了这样的一个结构:非整数步长的卷积(ConvTranspose,反卷操作), \(3\times 3\) ,步长1/2,256->128。反卷积之前试着使用过,但是由于(当时我以为)1/2步长时其输出只能为奇数,就没有深入了解了。结果此处碰上了,为了尽可能按照论文复现,重新了解了一下这个玩意。
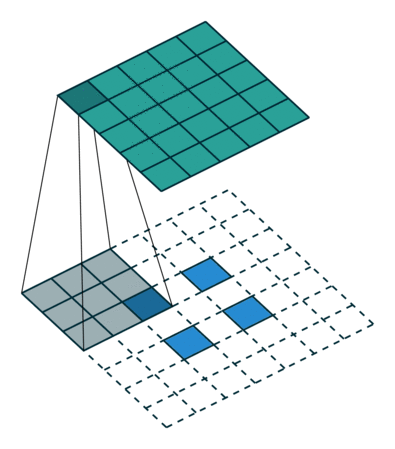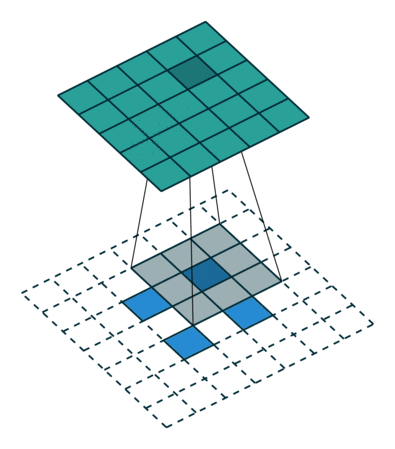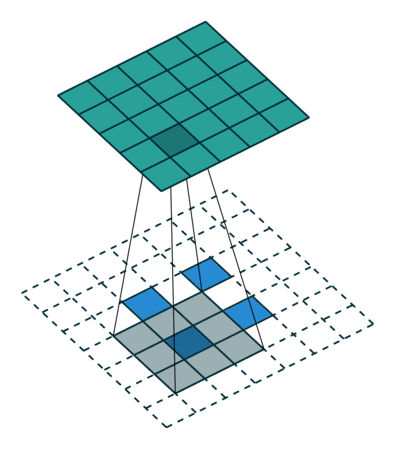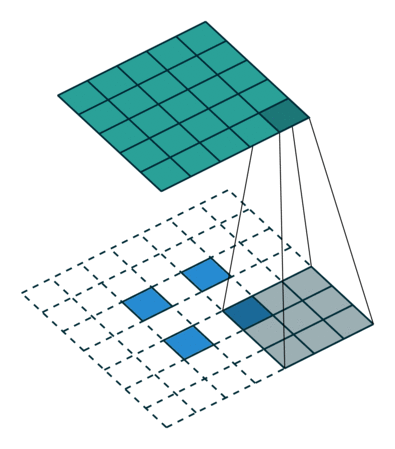
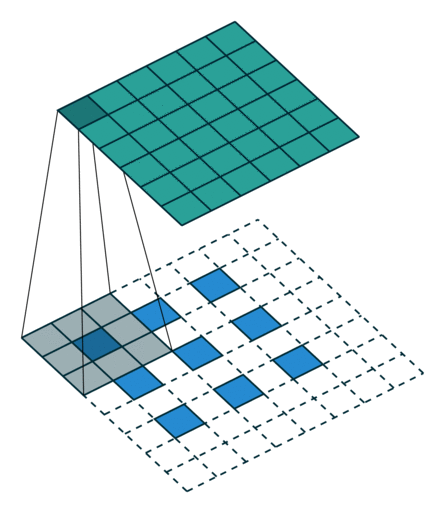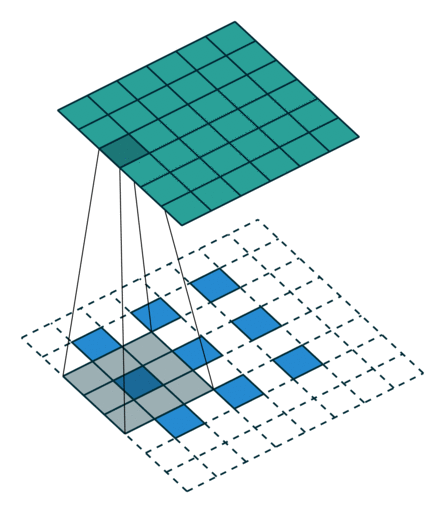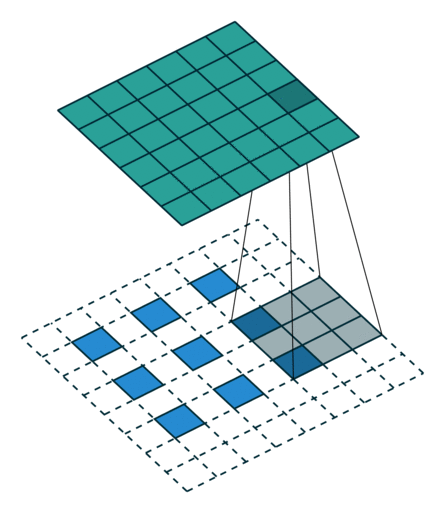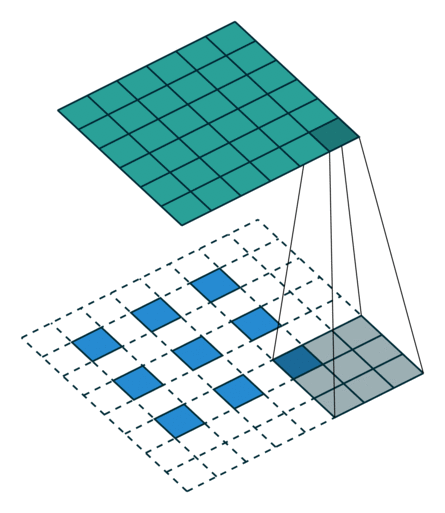
ConvTranspose就是卷积的逆过程,在有步长的情况下更为明显。常用于上采样放大。但实际上,即使步长为1,“放大”也是做不到的。由于ConvTranspose实际上也是用卷积核生成输出,卷积核必然导致输出小于输入,所以需要加入padding。padding让我感觉反卷积在放大过程中需要加入太多无效的信息(即使reflection padding也是一样的),毕竟是上采样过程(信息 少->多)。这种“无效信息的加入”在步长不为1的1时候更能体现出来(如下图片列表)
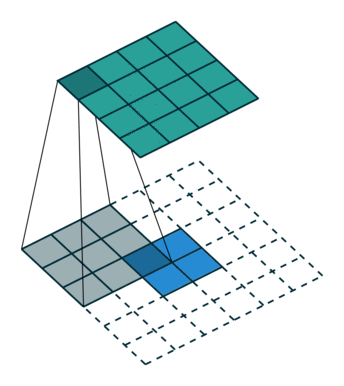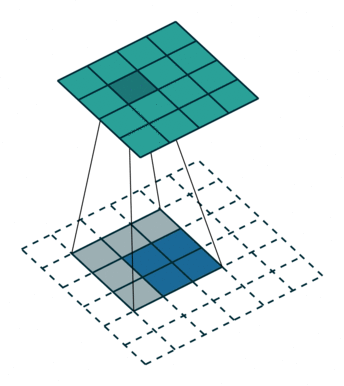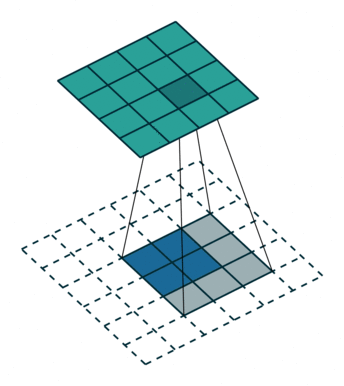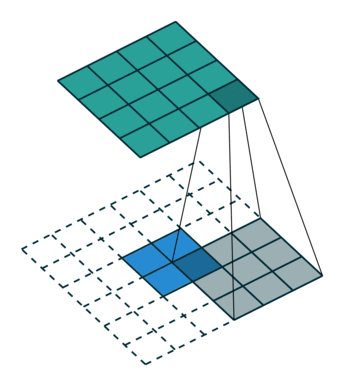 |
 |
 |
|---|---|---|
| padding放大 | stride放大(奇数) | stride放大(偶数) |
分数步长的卷积就是需要上采样的卷积。整数步长将会使卷积核跳过一些位点,而分数(小于1)则是需要在位点之间进行padding的。非1步长 / 有padding的卷积计算就不再赘述了。
值得注意的是分数步长的卷积,当步长不为1时(比如stride = 2),两个原始位点之间会填充一个位点。这样导致了:当stride = 2时,不管原来的输入size为奇数还是偶数,输出一定是奇数size的(此处说的是kernel size为奇数,个人感觉偶数的kernel size不够自然,需要讨论anchor)(偶数kernel size可以让输出为偶数,比如ConvTranspose2d(n, n, 4, 2, 1) 就是放大size为原来的两倍)。我实现的第一版CycleGAN使用的是ConvTranspose,附带了一个output_padding (由于当时使用奇数核),正如图三所示,感觉其结果十分不自然,但效率上并没有太大的区别。对于偶数kernel,其anchor默认在最左上方。
然而在第二版CycleGAN中我就把反卷积换成了卷积+上采样了,网络看起来更正常一些。
PatchGAN
这里指的是分类器设计,CycleGAN作者在其论文中采用了CycleGAN的结构,也就是分类器不输出二分类概率值,而是直接输出一个channel-1的卷积结果。例如,一个256*256的图像可以被一个70*70的特征图给表达,这70*70个元素,每个元素代表着图上的某个区域的真实性。自然我们希望,在判定为真实时这个输出接近ones(70, 70),反之接近zeros(70, 70)。论文中使用了70*70,我的实现中并没有这么做。我写的判别器结构:
- (256, 256, 3) -> (128, 128, 8) kernel size = 4,stride = 2,padding = 1,no norm
- (128, 128, 8) -> (64, 64, 16) kernel size = 4,stride = 2,padding = 1,instance norm
- (64, 64, 16) -> (32, 32, 32) kernel size = 4,stride = 2,padding = 1,instance norm
- (32, 32, 32) -> (16, 16, 1) kernel size = 4,stride = 2,padding = 1,no activation, no norm.
当然,如果要说的话,个人还有几个没有复现的部分:
- ResNet residual block我只用了两个。在论文中,128*128使用了6个resBlock,256*256则使用了9个。
- 没有避免model oscillation的trick(使用历史生成的图片而非当前最新生成的图片进行训练)
- 可能本征Loss是我加进去的东西,我在原文中并没有读出这样的意思来。(张麻子:这tm是复现?)
Normalization谈
首先看一张图(来自西交袁泽剑老师的CVPR课PPT,而PPT上的图又是来自【Wu and He, “Group Normalization”, ECCV 2018🔗】
上图描述了常用的(第四种我在写这篇文章之前也不知道是啥)4种norm(我目前见过用的只有BN与IN)。Normalization的作用就是神经网络的“白化操作”,将NN的输出固定于Norm(0, 1),可以稳定训练。
BN
BatchNorm看名字就应该能知道,这种Normalization与batch有关。看第一张图,当Batch size为N时,将会对某个channel做batch内的norm操作(也就是一个batch里的所有训练用例 + 一个channel的特征)。显然这个操作在batch size为1时意义不大(退化成了instance norm?)。类似于多张图片训练的(判别模型)常用这个。
IN
显然instance norm与batch没有关系,它是对单张图片意义上的norm。图片每个通道进行normalization。通道数对应了filter数,filter对应了生成的特征。实际上instance norm就是对不同的特征进行normalization。instance norm由于针对单张图片的不同通道,常用于生成式技术比如style transfer。
LayerNorm & GroupNorm
Laynorm 是一张图的所有通道做normalization。网上说是对RNN明显的,至于为什么,我没有深入了解过。而GroupNorm相当于是多个通道的Instance Norm,选取的通道数是可变的。
ResNet相关
ResNet专注于学习输入输出残差的表示,而不是学习简单的输入输出关系。为什么说学习残差?普通的CNN网络输入输出结构是这样的: \[ x\mathop{\rightarrow}^F F(x)\rightarrow y \] 学习的是x与y之间的映射关系,而在res net种,增加了一个identity mapping的合并: \[ x\mathop{\rightarrow}^F F(x)\rightarrow x',y=x+x' \] 那么,真正的输出是y,但是存在参数的部分输入输出只有x',也就是说学习的实际上只是y-x(输出 - 输入),也就是说:学习的是残差,残差表示将可以使深层网络收敛速度加快,并且网络过深时模型准确率并不会有太大的损失。实际上ResNet的 residual block结构也就是一个identical mapping和卷积的并联,个人在刚开始什么都不懂的时候,曾经将两个不同kernel size的卷积层并联在一起,觉得这会提高网络的表达能力(虽然不知道为什么,只是一种感觉)。所以CycleGAN为什么要使用ResNet结构?
个人的理解是:网络层数加深时,原始图的信息会在经过卷积发生损失,层数越深,积累的损失越大。加入直接的信息通道(shortcut)可以减少这样的信息损失。(可能个人原来使用不同的kernel size核并联时觉得,这样可以在同一层聚合不同大小的特征)。CSDN上有一篇文章说的很好(总结起来就是如下观点)[2]:
孙剑(?是我们学校的孙剑老师吗)认为ResNet可以避免梯度弥散问题(过深的网络优化时梯度不明显)
特征冗余可以被削弱:减少信息损失问题(和我的想法有点类似)
ensemble 特征融合:实际的网络层数由于shortcut的加入变得并不太深
层次性:shortcut保留了简单的特征,与复杂的特征(参数卷积部分)融合
凸函数性:层数越深,函数非凸性越严重,找不到全局最优,ResNet结构可以优化函数非凸性
一些细节问题
- 关于激活函数:Sigmoid通常用于概率映射,Tanh通常用于图像输出层,而ReLU和LeakyReLU通常作为中间层的输出函数。注意不要乱加。
- 为什么有的时候输入层会倾向于不进行normalization?很显然,输入的数据会进行预处理,通常都在DataLoader的transform中。比如说使用normalize,以及shuffle,就已经可以保证数据的标准高斯分布。这种情况下,第一层是不需要进行normalize的。
- Conv2D不提供padding的模式变换(same和circular选项不算),需要在nn模块下使用ReflectionPad / ZeroPad 等等Padding方式。
参考文献
[1] Jun-Yan Zhu, Taesung Park, Phillip Isola, Alexei A. Efros Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks.
[2] Ian J. Goodfellow, Jean Pouget-Abadie∗ , Mehdi Mirza, Bing Xu, David Warde-Farley, Generative Adversarial Nets
[3] 《ResNet个人理解》https://blog.csdn.net/nini_coded/article/details/79582902