SVM算法与实现
SVM
Preface
SVM (Support Vector Machine 支持向量机) 曾一度导致深度学习的退潮(1995)。Geoffrey Hinton提出BP之后,遇到了sigmoid激活函数梯度消失问题,恰好此时Vapnik提出统计学习理论,正式提出非线性SVM并将其应用,使得这个分类器盛行了20年?直到DL的梅开三度。 恰好大三下学期有《模式识别》课,且有学长说他考前每天必推一遍SVM原理,不如现在趁《运筹学》还热着,尝试自己推导一遍,并实现这一个经典算法。
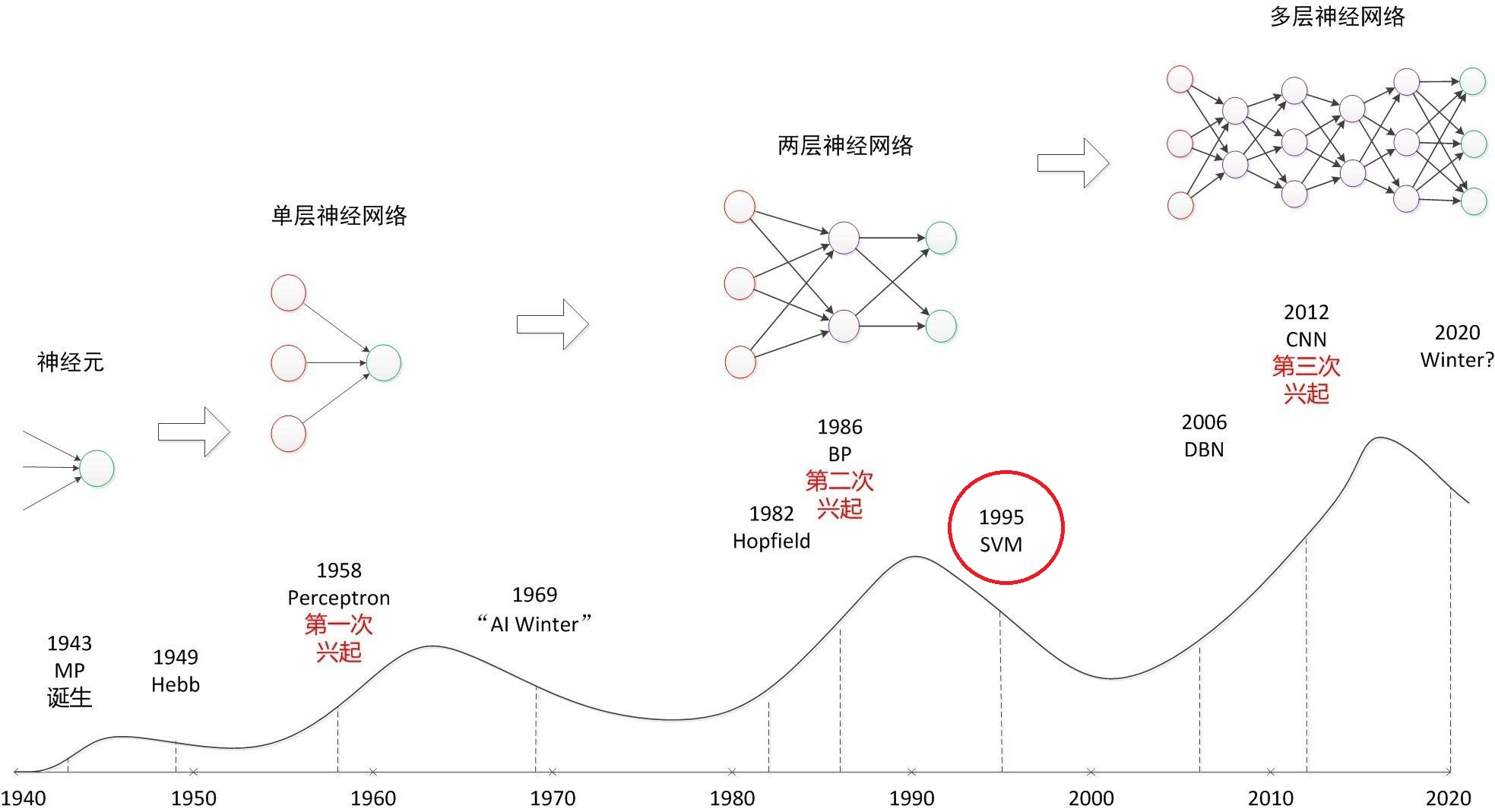
SVM作为经典的“最大间隔”(maximum margin)分类器,除了其精巧的数学变换(Lagrange对偶,可能是因为我自己推出来了所以觉得很妙吧:laughing:)之外,“支持向量”的思想是最妙之处。这种方法大大减少了训练时使用的维数,避免了内存爆炸问题,并且可以使用少量样本进行训练。
超平面的意义
假设一个平面,其到原点的法向量为\(\pmb{w}\),到原点的距离为\(b\),那么平面方程应该是: \[ \begin{equation}\label{equ:hyper} \pmb{w}^T\pmb{x}+b=0 \end{equation} \] 实际上这是方程: \[ \begin{equation}\label{equ:plain} Ax+By+Cz+....+b=0 \end{equation} \] 进行的推广,那么对于公式\(\eqref{equ:hyper}\),如此定义方式为什么可以定义一个平面?x为什么一定在一个由\(\pmb{w}\)以及\(b\)定义的唯一平面上?推导如下,如图(1),过原点做垂直于超平面的垂线,设交点为P,平面上一点x相对于P点的相对向向量为x'。那么有: \[ \begin{align} & \pmb{v}=\vert b\vert\frac{\pmb{w}}{\Vert\pmb{w}\Vert} \\ & \pmb{x}=\pmb{x}'+\pmb{v} \\ & \pmb{w}^T\pmb{x}+b = \pmb{w}^T\pmb{x}'+\pmb{w}^T\pmb{v}+b = 0 \end{align} \] 推导还是比较简单的。
如果要推算一个点到超平面的距离,比如上图的点y到超平面的距离,相当于是:y交超平面于y'点,而由于y'在超平面上,于是有\(\pmb{w}^T\pmb{y}'+b=0\),那么由于\(\pmb{y} = \pmb{y}'+\pmb{y}''\),那么可以知道: \[ \begin{equation}\label{equ:predist} \pmb{w}^T\pmb{y}+b=\pmb{w}^T\pmb{y}'' \end{equation} \] 而公式\(\eqref{equ:predist}\)右侧相当于是y''在未单位化的方向向量上的投影,单位化之后可以得到距离。那么整个点到超平面距离公式如下: \[ d = \frac{\vert \pmb{w}^T\pmb{x}+b\vert}{\Vert \pmb{w}\Vert} \]
目标函数导出
对于一个二分类的SVM,我们希望找到一个超平面,能够最优地将两类数据分开。如下图所示,图片来源见reference[1]。
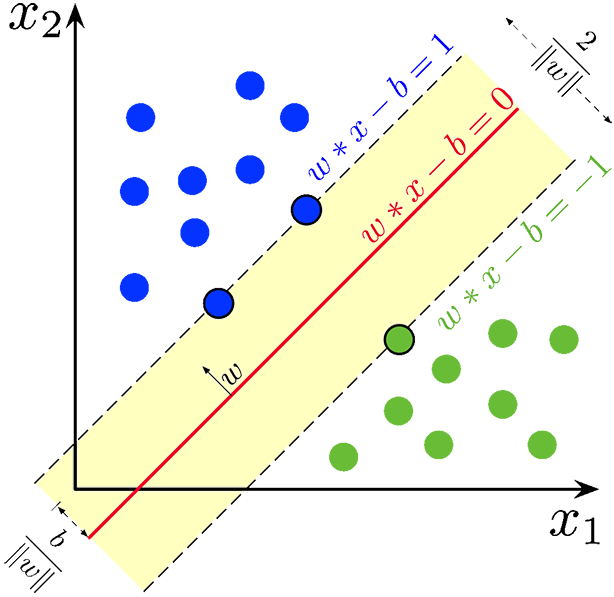
联系以下其他的分类方法,比如说LDA(Linear Discriminative Analysis),在算法构建时就存在一点就是:使类间方差是最大的。也就是希望两类之间的间隔是最大的。在SVM中,不衡量类间方差,衡量的是“margin”(就是Figure 3中的黄色区域)。
从简单的例子引入,我们讨论二分类线性分类器。对于一个线性可分的待分类数据集,两个类别间需要找一个超平面。显然,两个类别都会有离这个超平面距离最近的数据点,这个最短距离(表征的是一种错误容限,如果为0则恰好在不可判定的边界上)如果记为\(d_1, d_2\)的话,我们显然是希望\(d_1, d_2\)尽可能大的(最容易出现错误的数据点(离分类超平面最近的点)离分类界限越远)。像这样可以定义超平面所在位置的数据点(最容易出现分类错误,最应该被讨论),被称为“支持向量(support vector)”,此后讨论的都是支持向量确定的超平面间的距离间隔。如何衡量这个距离?显然可以使用几何距离的推广(维数上的推广)。可以通过2-范数来定义空间中两个点之间的距离,但由于这是点与平面之间的距离,需要点与平面的距离公式。
从我们上面所说的:“希望最可能分类错误的数据点对应的最短超平面距离间隔-是-最大的”这个想法上来看我们应该将距离的生成分为两步:
- 给定超平面时,如何衡量哪个数据点是最容易分类错误的?
- 在给定支持向量时,如何进行超平面参数的确定与优化?
开始时个人感觉,这个问题有点自循环的感觉。超平面确定依赖支持向量?支持向量给定后才能确定超平面参数?这不就产生了鸡生蛋 蛋生鸡的悖论了吗?有关这个问题的讨论,在处理完目标函数的数学变换之后我再从数学的角度上谈一下我个人的理解。
距离衡量
对于一个二分类问题,超平面已经定义为:\(\pmb w^Tx+b = 0\),那么如果所有数据都能正确分类,两个数据集的数据点一定会呈现:一个类别的数据在超平面的“上方”(正方向上),另一个类别则全部在“下方”。相应地,\(\pmb w^Tx+b\)可能大于0或者小于0。也就是说: \[ \left\{ \begin{array}{l} \pmb w^Tx+b > 0,\large{\text{正类}} &\\ \pmb w^Tx+b < 0,\large{\text{负类}} & \end{array} \right. \] 而很明显,我们的样本点是有限的,也就是说,每个一定会存在一个点,在正类中,正值最小,负类中赋值最小。那么可以根据这两个最小值进行尺度归一化: \[ \left\{ \begin{array}{l} \pmb w^Tx+b \ge 1,\large{\text{正类}} &\\ \pmb w^Tx+b \le -1,\large{\text{负类}} & \end{array} \right. \] 那么使用一个小trick,用sgn(·) 函数处理以上式子: \[ \begin{equation}\label{equ:dist} d_f=y_i(\pmb w^Tx+b),\text{ where } y_i =1 \text{ if 正类 otherwise } y_i = -1 \end{equation} \] 这样可以保证:\(d_f\)在分类正确时恒为正值,并且让问题尽可能简单化。(\(y_i\)当然可以不取正负1,但是取其他的值让问题形式稍微复杂了一点点,没有什么必要)。根据在之前小节讨论的超平面距离公式,已知\(\vert\pmb w^Tx+b=1\vert\)(对于支持向量而言),那么两个类距离超平面的距离是各为\(1/\Vert\pmb{w}\Vert\)。那么优化问题即为: $$ \[\begin{equation}\label{equ:simple} \left\{ \begin{array}{l} \text{max }\frac{2}{\Vert\pmb{w}\Vert} &\\ \text{s.t. } y_i(\pmb w^Tx+b) \ge 1, \text{ for } i\in1,2,...n & \end{array} \right. \rightarrow \left\{ \begin{array}{l} \text{min }{ \frac 12 \Vert\pmb{w}\Vert^2} &\\ \text{s.t. } y_i(\pmb w^Tx+b) \ge 1, \text{ for } i\in1,2,...n & \end{array} \right. \end{equation}\] $$ 理想情况下,需要优化的问题就是按照公式\(\eqref{equ:simple}\)定义的。
非理想情况
哪有那么多线性可分的数据集?分类错误在大多数情况下都无法避免(他们中出了一个叛徒)。原有的线性可分条件太强了,需要进行一定的松弛才具有泛化能力。聪明的数学家们想到的办法是:设定一个容限\(\zeta_i\),也就是一个松弛因子,不追求找到最小的那对。反之,我们需要在超平面间隔宽度以及允许的错分类深度(某个数据集误入敌营的距离)之间进行权衡。
由于\(y_i(\pmb w^Tx+b) \ge 1\)很难达成,那么总可以\(y_i(\pmb w^Tx+b) \ge 1 - \zeta_i,\zeta_i \ge 0\)吧。那么,所有\(\zeta_i\)的和(它们都是非负的)显然反映了对这个分类器的松弛程度。问题就在于,我们希望 松弛一点,泛化能力强一点?还是严格一点,正确率高一点?通过一个可调的系数来决定: \[ \sum_{i=1}^n\zeta_i+\frac{\lambda}{2}\Vert\pmb{w} \Vert^2 \] \(\lambda\)就是起权衡作用的加权系数。
目标函数数学变换
松弛后的问题原目标函数表达式如下: \[ \begin{equation}\label{equ:tar1} \left\{ \begin{array}{l} \text{min } \frac 1n \sum_{i=1}^n\zeta_i+\frac{\lambda}{2}\Vert\pmb{w} \Vert^2 &\\ \text{s.t. }y_i(\pmb{w}^T\pmb{x}_i+b) \ge 1-\zeta_i,\zeta_i\ge0\text{ for }i\in1,2,...n &\\ \text{where } \zeta_i \text{ is max} (0, 1-y_i(\pmb{w}^T\pmb{x}_i+b)) & \end{array} \right. \end{equation} \] 由于这是一个多变量有约束优化问题。可以使用Lagrange乘子法写出其Lagrange乘子函数。根据运筹学学过的知识(运筹学 第三章第五讲 有约束最优化问题的KKT方法):
需要注意的是,虽然\(\zeta_i \text{ = max} (0, 1-y_i(\pmb{w}^T\pmb{x}_i+b))\)成立,\(\zeta_i\)仍然是一个人为选取的参数,用于规定:第i个数据点相对边界的偏离(进入错误分类区的深度)大小容许值,所以实际上\(\zeta_i\)并不是\(\pmb{w}\)或者\(b\)的函数。 \[ \begin{equation}\label{equ:lag} L(\pmb{w},b, \zeta_i,\lambda_i,\mu_i)=\frac 1n \sum_{i=1}^n\zeta_i+\frac{\lambda}{2}\Vert\pmb{w} \Vert^2-\sum_{i=1}^n\lambda_i[y_i(\pmb{w}^T\pmb{x}_i+b)+\zeta_i-1]-\sum_{i=0}^n\mu_i\zeta_i \end{equation} \] 则由KKT条件,需要对\(\eqref{equ:lag}\)定义的\(L(\pmb{w},b, \zeta_i,\lambda_i,\mu_i)\)进行微分操作。也即所有偏导数都应该是0: \[ \begin{align} &\frac{\partial L}{\partial \pmb{w}} = \lambda\pmb{w} - \sum_{i=1}^n\lambda_iy_i\pmb{x_i} = 0\rightarrow\lambda\pmb{w} =\sum_{i=1}^n\lambda_iy_i\pmb{x_i}\label{equ:pw}\\ &\frac{\partial L}{\partial b} =\sum_{i=1}^n \lambda_iy_i = 0\label{equ:pb}\\ &\frac{\partial L}{\partial \zeta_i} = \frac 1n -\lambda_i-\mu_i = 0\label{equ:pz} \end{align} \] 将公式\(\eqref{equ:pw}\eqref{equ:pb}\eqref{equ:pz}\)带入到公式\(\eqref{equ:lag}\)中,可以得到Lagrange对偶问题,显然有: \[ \begin{align} &\sum_{i=1}^n\lambda_i[y_i(\pmb{w}^T\pmb{x}_i+b)+\zeta_i-1] = 0 \quad\text{(KKT条件)}\\ &\begin{array} &L=\sum_{i=1}^n(\frac 1n-\lambda_i-\mu_i)\zeta_i+\frac{\lambda}{2}\Vert\pmb{w} \Vert^2-\sum_{i=1}^n\lambda_iy_i(\pmb{w}^T\pmb{x}_i+b)+\sum_{i=0}^n\lambda_i\\=\frac{\lambda}{2}\Vert\pmb{w} \Vert^2-\sum_{i=1}^n\lambda_iy_i\pmb{w}^T\pmb{x}_i+\sum_{i=0}^n\lambda_i \end{array}\\ &L=\frac{1}{2\lambda}\left (\sum_{i=1}^n\lambda_iy_i\pmb{x_i}\right)^T\sum_{i=1}^n\lambda_iy_i\pmb{x_i}- \frac{1}{\lambda}\sum_{i=1}^n\lambda_iy_i\left(\sum_{j=1}^n\lambda_jy_j\pmb{x_j}\right)^T\pmb{x}_i+\sum_{i=0}^n\lambda_i \end{align} \] 最后化简得到,相对于原问题(Primal),此为Lagrange对偶问题,注意在对偶讨论下,需要进行最大化。 \[ \begin{equation}\label{equ:dual} L'(\lambda_i)=\sum_{i=0}^n\lambda_i - \frac{1}{2\lambda}\left (\sum_{i=1}^n\lambda_iy_i\pmb{x_i}\right)^T\sum_{i=1}^n\lambda_iy_i\pmb{x_i} \end{equation} \] 约束条件如何变换?也就是此处每个\(\lambda_i\)的约束条件是?首先,公式\(\eqref{equ:pb}\)定义的约束没有能够带入原问题中,于是称为对偶问题的一个约束项,并且\(\lambda_i\)本身就是大于等于0的。那么它有上界吗?有的,由于公式\(\eqref{equ:pz}\)中\(\mu_i\)是非负的,可以得到: \[ \begin{equation}\label{equ:cond} \text{s.t. }\sum_{i=1}^n \lambda_iy_i = 0 \text{ and } 0\le\lambda_i\le\frac 1n \end{equation} \]
而实际上,只要能求出公式\(\eqref{equ:dual}\)对应的对偶问题的解(\(\lambda_i\)),也就可以根据公式\(\eqref{equ:pw}\)计算出\(\pmb{w}\),而由所有的support vector以及\(\pmb{w}\)可以求出b,也就唯一确定了超平面。之所以进行对偶变换,是因为原问题太难以讨论了,原问题并不是简单的二次规划问题,并且存在烦人的\(\zeta_i\),约束条件也令人难受,而对偶之后,约束变成了线性的,并且目标函数的形式变得简单了,可以使用一些二次规划的算法求出\(\lambda_i\)。
逻辑自循环?
开始我对这个算法的思想非常不理解。我起初认为:
- 给定了超平面,才知道不同类别中哪个数据点距离超平面最近
- 给定了支持向量,才能求出超平面参数来(间隔最大嘛)
这两点看起来就跟悖论一样,解决其中一点仿佛是要基于另一点的解决。但最后我们化简得到的目标函数却很有趣:\(\eqref{equ:dual}\)中并没有出现【(1)超平面参数(2)选谁为支持向量 】的信息。
解开这个“自循环”的关键在于对偶问题的\(\lambda_i\),对偶问题的解决确实是不依赖于以上信息的,它是根据所有的训练样本点优化出来的,而这个\(\lambda_i\)实际上就蕴含了支持向量的信息。假设\(\lambda_k = 0\),由公式\(\eqref{equ:pw}\)知,样本\(x_k\)就不影响\(\pmb{w}\)的计算了,也就是说\(x_k\)就不是支持向量。\(\lambda_i\)不为0的数据才是我们需要的支持向量,他们才参与计算,决定超平面。
也就是说:算法的推导逻辑有赖于这样的一个“逻辑自循环”,因为只要循环之中的一个环节被解决了,另一个环节也就随之解决了。而通过巧妙的数学变换,我们可以找到绕开“自循环”的方法,通过优化先求出蕴含了支持向量选取意义的\(\lambda_i\),再求出超平面参数\(\pmb{w},b\)。
SMO 二次规划求解
SMO(Sequential Minimal Optimization)[3] 是一个SVM算法对偶问题的快速计算方法,它可以极大地减小内存空间消耗,并且其解是解析的,而不需要对QP对偶问题\(\eqref{equ:dual}\)进行复杂的数值解计算。SMO的两大精髓思想是:
- 参数迭代计算“分治”得到一个个的QP sub-problems,每个sub-problem只需要解一个两参数QP优化问题。
- 使用一个启发式算法,选择每次进行迭代的两个参数。
由于论文[3]中,启发式算法部分我没怎么看懂,只看懂子问题分割部分,所以在接下来的算法实现过程中,只实现非启发式(随机的)参数选择,也就是一个非启发的SMO,效率上可能会低一些。
In order to speed convergence, SMO uses heuristics to choose which two Lagrange multipliers to jointly optimize.
有关KKT条件不满足点的删除以及非边界点的处理这里没有看懂(不是很清楚这样做的理由究竟是什么,可能对KKT条件的理解不够深入吧,不太能想清楚 不满足KKT条件对优化的影响)。所以整个2.2小节读完之后,在实现中都略过了。
Kernel 非线性
为了使讨论不失一般性,上来就应该讨论核函数表示下的SVM,而非之前小节中推导的线性SVM(线性SVM也就是核函数是标准内积的情况)。
之前我们介绍的都是标准内积核,也就是两个向量直接进行内积操作。在公式\(\eqref{equ:dual}\)中,用到了内积,因为公式\(\eqref{equ:dual}\)实际可以写为: \[ \begin{equation}\label{equ:dot} L'(\lambda_i)=\sum_{i=0}^n\lambda_i -\frac{1}{2\lambda}\sum_{i=1}^{n}\sum_{j=1}^n\lambda_i\lambda_jy_iy_j\pmb{x}_i^T\pmb{x}_j \end{equation} \] 而直接内积对应的是线性的空间。如果对x做非线性变换,达到空间变换的目的,在变换后的空间下是线性的超平面,但在原空间下已经变成别的形状,使得原本线性不可分的数据在新空间下可分。 \[ \begin{equation}\label{equ:kernel} k(\pmb{x}_i, \pmb{x}_j)=\phi(\pmb{x}_i)\phi(\pmb{x}_j) \end{equation} \] 公式\(\eqref{equ:dot}\)中的内积项替换为公式\(\eqref{equ:kernel}\)的核函数即可。
参数“分治”
SMO算法在干什么呢?个人感觉这有点像coordinate descent,但是感觉简单的coordinate descent无法胜任SVM对偶问题的求解。因为式\(\eqref{equ:cond}\)中定义了线性约束,coordinate descent没有办法直接满足线性约束。在论文中(SMO算法论文),作者也说到 问题的最小讨论参数个数为2,因为只讨论一个参数时无法满足线性约束条件。于是作者真就两个两个参数进行讨论,作者说到:
The advantage of SMO lies in the fact that solving for two Lagrange multipliers can be done analytically.
确实如此,并且这个解析解的推导还算比较简单。由于SMO中sub-problem求解的论文思路是比较清晰的,在此处只简单回顾一下论文的方法。
I. 约束确定
由于只选取两个参数,维度好低啊,可以进行可视化。注意我自己的推导和《模式识别》书以及SMO论文上的问题形式均不同,书以及论文均是\(C\)定义的,也就是下式定义的loss,为了与论文一致,我现在就讨论公式\(\eqref{equ:book}\))定义的loss导出的对偶问题: \[ \begin{equation}\label{equ:book} C\sum_{i=1}^n\zeta_i+\frac{1}{2}\Vert\pmb{w} \Vert^2 \end{equation} \] 由约束项\(\eqref{equ:cond}\)结合下图可以看出,选取的\(\alpha_i(即\lambda_i),\alpha_j\)的线性约束与constatnt值约束在二维情况下很简单。分\(y_i==y_j\)是否为true两种情况来看,每种存在两个情况(论文中每种只画出一条线性约束的可视化图,红线是我后来加上的):
每次只需在这斜率为\(\pm1\)的线段上求约束极小值(二次函数(线性核)或是其他凸问题(非线性核))即可。
II. 极值求解
显然,由于只有两个参数时,根据线性约束,一个参数可以使用另一个参数表示,使得我们可以先更新一个参数,再根据更新值求另一个参数的值,完成迭代。那么在求其中一个参数时,根据线性约束,问题就优点类似于coordinate descent了。
- 首先确定带优化参数的值区间(L, H)
- 求一维最小值问题的极值点\(\alpha^{new}\)
- \(\alpha^{new}\)可能不在(L,
H)范围内,根据单峰以及凸性需要进行clipping
- \(\alpha^{new} > H\),则最小值在H处取得
- 反之\(\alpha^{new}<L\)则最小值在L处取得
- 否则 \(\alpha^{new}\in(L,H)\),最后的极小值点就是\(\alpha^{new}\)
\[ \begin{equation}\label{equ:update} \alpha_2^{new}=\alpha_2+\frac{y_2(E_1-E_2)}{\eta}\\ \text{where } \eta = k(\pmb{x}_1, \pmb{x}_1)+k(\pmb{x}_2, \pmb{x}_2)-2k(\pmb{x}_1, \pmb{x}_2) \end{equation} \]
此处\(\eta\)是公式\(\eqref{equ:dot}\)在核函数替换下的目标函数的 二阶导。E则是预测误差\(u_{pred}-y_i\)。感觉更新式\(\eqref{equ:update}\)有点像牛顿法的迭代过程。则根据线性约束,\(\alpha_1\)更新后的值也可以写出来。
III. 计算需要的结果
每一步\(\alpha_1,\alpha_2\)更新都可以根据新的值计算一次\(\pmb{w},b\)。当所有参数计算完毕之后,算法也就结束了。\(\pmb{w}^{new}\)怎么来的很好懂,而\(b\)的更新迭代过程相对麻烦一些。由于\(b=\pmb{w}^Tx_i-y_i\)成立,在kernel存在的情况下,b是: \[ b=\left[ \sum_{i=1}^n\lambda_iy_ik(\pmb{x}_j, \pmb{x}_i) \right] -y_i \] 根据上式进行更新,写出相对值表达式即可。
实现SMO算法
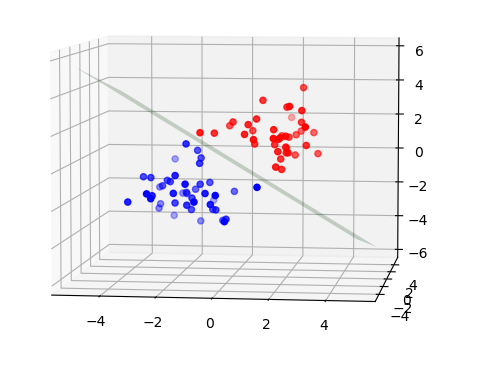
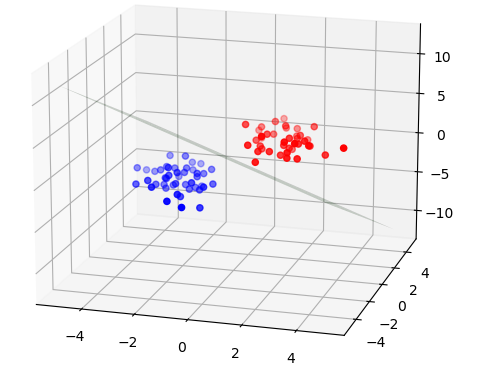
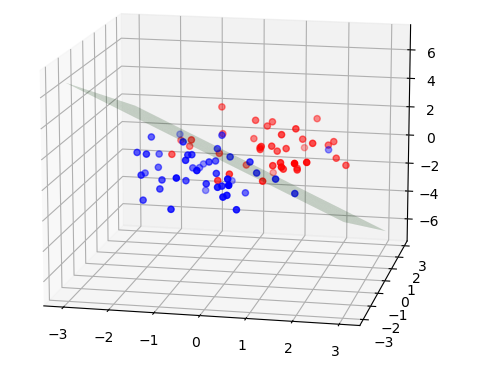
论文中给出了 给定两个数据时计算的伪代码。按照论文进行实现,代码见Github Repository 🔗:TorchLearning,结果如下:
 |
 |
|---|---|
| 距离适中 | 距离较远 |
 |
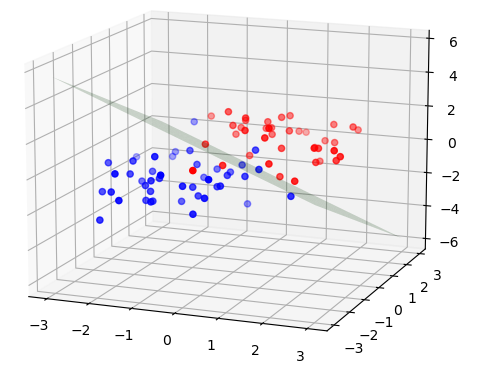 |
| 存在较大重叠 | 存在较小重叠 |
在使用不同的随机数据进行超平面求解时发现,存在当C过大时,导致计算的超平面完全错误的问题。SMO算法的收敛速度看起来极快,通常只需要迭代3-6次就能收敛。注意,在这里数据点并不算多:
- 维数3,正负类总和只有84个样本。
其他的讨论
空间变换
之前我就听说,SVM是将低维数据升维到高维空间,低维中不好进行分类的数据,高维下可能可以很好分开。但是读完原理,实现完代码之后也没有发现哪里有维度的升高。
实际上,维度的升高在核函数中“有所体现”,在【这篇文章】中,作者提到:
那我们我们是否可以将数据映射到高维空间呢?即创建一些新的特征。我们可以创建特征 \(x_3=x^2,x_4=y^2\)
虽然看起来维数从(x, y)变为了\((x, y, x_3, x_4)\),但是\(x_3,x_4\)并不是独立的维度,个人倾向于认为这是在原空间对数据的空间分布进行了变换。比如说将两类环形(同心圆)分布的数据变换到相同维度的另一个空间下,但是在这个空间下两类数据是线性可分的。当然,非要说这是高维空间,应该也可以吧。
核函数方法固然是线性的非线性迈出的一大步,但是个人感觉核函数的选择有赖于数据的空间分布。在不明分布的情况下,随意选择核函数将会造成分类能力的下降,靠人工比较选择显然不是个很好的办法。
多分类问题
SVM是典型的二分类分类器,但我们用的SVM却有多分类的能力。关于多分类,个人的想法是:
- 对每个类,只需要区分本类和其他即可。构建一个个的本类以及其他类的二分类问题应该就可以。
维基上说:
Building binary classifiers that distinguish between one of the labels and the rest (one-versus-all) or between every pair of classes (one-versus-one).
个人更倾向于one-versus-one形式的。在《模式识别》一书上介绍了如何处理多分类问题(感觉像是one-versus-all形式的)。而one-versus-one存在这样的特点(个人认为):
- 实现简单,不需要做过多算法改动,可以直接由多个二分类SVM组合(优点)
- 内存/计算资源消耗大,每两个数据类别之间都需要计算/储存一个\(\pmb{w},b\)(缺点)
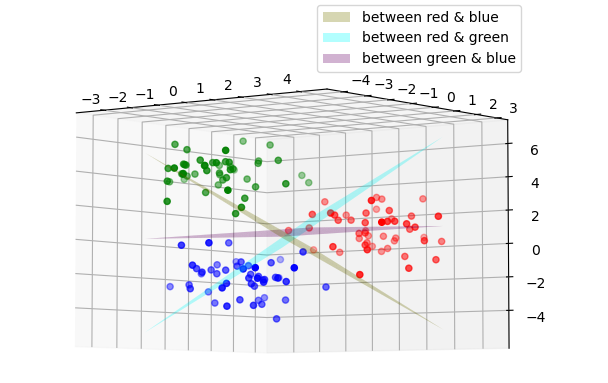
根据one-versus-one思想以及二分类SVM构建的一个多分类SVM结果如下(只画出超平面 / 数据),如果需要进行predict,predict思想如下:
- 求所有的二分类SVM predict,对每一类进行累加(可以用一个list保存每一类累加结果)
- 取累加值最大的类(简单的想法,对于一个数据点,其落在正确的类中时,在每个二分类SVM中的输出应该都为1)作为predict值。
Reference
[1] By Larhmam - Own work, CC BY-SA 4.0,link🔗
[2] Wikipedia, Support-vector machine
[3] Platt, John (1998). "Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines"
[4] 张学工(编著),模式识别(第三版),清华大学出版社