滤波&卡尔曼
Filtering & Kalman
I. 引入
2021赛季充分认识到滤波的美妙之处。虽然只前学了DSP,但是在进行实际系统控制的时候,很少有意识地进行滤波或者平滑。2020赛季中设置过一个静止目标滑动平均,在此前没有做过非常大量的滤波。
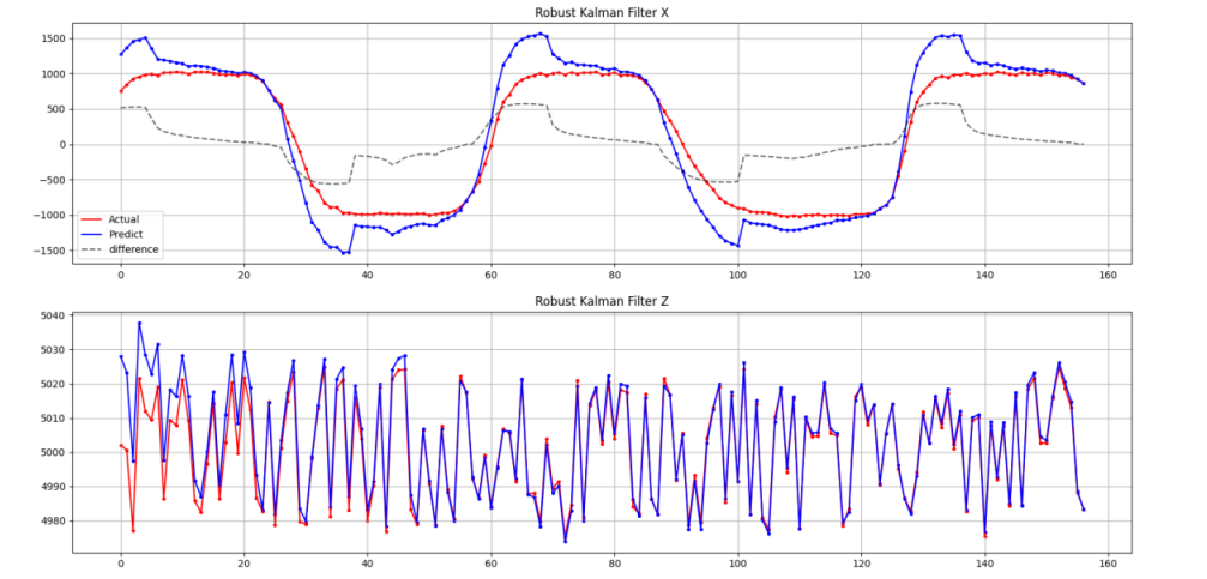
本文是对近段时间使用的滤波方法进行的一个比较肤浅的总结,包括:
- ARKF(自适应抗差KF)
- MEE & CMEE(约束最小误差熵KF)
- ESKF(Error State KF)
II. ARKF
2.1 理论分析
2.1.1 抗差
ARKF[1]是很老的工作了,大创答辩的时候老师还特地问我为什么要引那么老的文献(1999,比我还大)(小声:但人家简单有效啊)。我已经在[优雅线代与美妙优化]一文中说了,卡尔曼滤波是怎么与最小二乘联系起来的。这里简单回顾一下: \[ \begin{equation}\label{lsp} W(k){x}(k)+\xi(k)=Y(k) \end{equation} \] 其中\(W(k)\)(实际是上面那篇博客中提到的\(X(k)\),但是\(X\)用于表示非状态矩阵,容易与\(x\)发生冲突)以及\(Y(k)\)的意义直接看上面提到的博文吧。\(\xi(k)\)则是状态转移噪声 / 观测噪声concatenation的白化变换。我们提到,KF实际上是根据\(\eqref{lsp}\)进行MSE最小化的过程。
但是MSE在很多问题下的表现并不好,特别是外点很多的时候。想想在最小二乘直线拟合的时候,一个外点就能让直线拟合出来的参数变得比原来离谱很多,这是由于误差函数的性质决定的:MSE对偏差大的数据产生的cost是平方级别的cost,而Huber则是线性的cost。
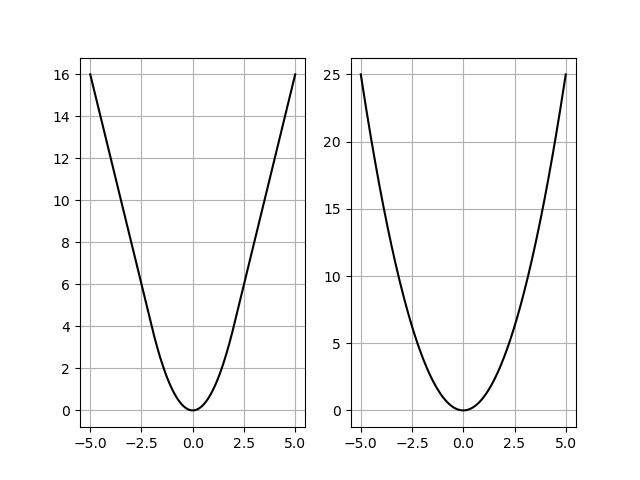
这就决定了Huber函数存在一定的外点鲁棒性,对于外点多的数据,Huber函数的KF将会更加稳定。但是很可惜,由于Huber函数的表达式比MSE复杂,并且原始Huber函数是存在非线性的(if判定,虽然导数以及原函数是连续的),我个人没有推出其解析解(我也没推,我也不会Mathematica),所以对于公式\(\eqref{lsp}\)定义的“状态转移”,由于公式\(\eqref{lsp}\)展开是: \[ \begin{equation}\label{optim} \begin{pmatrix} I\\ H \end{pmatrix}\breve{x}(k)= \begin{pmatrix} A\hat{x}(k-1)\\ z(k) \end{pmatrix} + \begin{pmatrix} w(k)\\ v(k) \end{pmatrix}= \begin{pmatrix} A\hat{x}(k-1)\\ z(k) \end{pmatrix} + E(k) \end{equation} \] 其中'\(\breve{}\)'表示先验,'\(\hat{}\)'表示后验,我们需要估计的是公式\(\eqref{optim}\)中的\(\breve{x}(k)\)(也就是KF需要估计的当前状态,实际就是公式\(\eqref{lsp}\)的\(x(k)\)),那么\(x(k)\)可以写为: \[ \begin{equation}\label{optim2} x(k)^*=\mathop{\arg \min}_{x(k)}\sum \Phi(y_i-w_i^Tx(k)) \end{equation} \]
此处,\(w_i^T\)是公式\(\eqref{lsp}\)中提到的矩阵\(W(k)\)的第i行。\(\Phi(·)\)是鲁棒核函数,此处可以为Huber。普通卡尔曼滤波则此处为\((·)^2\)函数,平方则是存在闭式解的,甚至可以不用化为求和式,只需要简单用pseudo逆就可求出。
而由于\(y_i,w_i\)都是已知的,具有具体的意义,只剩下未知的待估计位姿\(x(k)\),那么只需要求解公式\(\eqref{optim2}\)定义的优化问题即可。这步在Kalman滤波中称为:抗差(Robust)化,因为解抗差最小二乘问题得到的解将更加稳定。
2.1.2 自适应
朴素KF的噪声协方差不是自适应的,而是开始就设置好的。Q和R两个矩阵,一个代表状态转移噪声协方差,另一个代表观测噪声协方差,都是固定的(非自适应,固定就意味着高斯噪声假设)。这两个矩阵的意义比较明确:反映了不同的物理过程的噪声大小。比如:
- 若要让结果倾向于数学模型(状态转移模型),那么状态转移噪声应该显著小于观测噪声。
- 如果要让结果倾向于观测(观测模型),那么观测噪声应该显著小于状态转移噪声。
但是实际使用中,关于【状态转移 / 观测两者谁更可靠】的问题是非常不好回答的。我可以凭借先验知识来判定,状态转移更好还是观测更好,但是这也仅限于“定性判定”,此后的KF甚至还需要进行调参,才能得到较好的收敛结果。此外,两个噪声协方差的固定性限制了我们可以处理的噪声种类(只能是高斯噪声),显然限制了KF在某些问题下的泛化。自适应的过程可以认为是:
使得KF可以处理的噪声类型摆脱高斯噪声限制
作者使用的是中值偏差(median deviation)。说实在的,这个median deviation公式可以说是很奇怪了: \[ \begin{equation}\label{med} \hat{d}(k)=\text{median}\vert \frac{r(i)-\text{median}(r(i))}{0.6745}\vert \end{equation} \] 其中,\(r(i)\)是滑动窗口内的一个新息(innovation),其实就是偏差:\(z(i)-Hx(i)\)。所以这做的是什么?相当于是:计算误差协方差时(尤其是方差计算),本身是可以通过标准差(standard deviation)计算出来的,但是可以计算标准差的替代品(别的deviation)。而此处,新息的最优估计也使用了鲁棒核函数: \[ \begin{equation}\label{innov} r^*(k)=\mathop{\arg\min}_{\hat{r}(k)}\sum^{k}_{i=k-N+1}\Psi\left(\frac{r(i)-\hat{r}(k)}{\hat d(k)}\right) \end{equation} \] 即,已知一个滑动窗口内的所有新息的信息\(r(i)\),根据中值偏差进行的re-scale操作加权 + Huber鲁棒核函数,优化这个问题,得到新息的最优估计,根据新息计算噪声水平。
2.2 代码
代码可见[Github🔗:Algorithm-Plus/KF]。其中KFTest.cc是对一个带有运动噪声的小球进行的仿真,使用的就是ARKF。当前效果已经比传统KF稳定了很多(不过同时也结合了很多简单滤波器)。
III. MEE & CMEE
[2]。这是KF最近的工作,使用EE(Error Entropy)替换原来的MSE / Robust MSE准则。实际上,这些人关于KF的想法就是:
- 粒子滤波太慢了,但是它很棒,可以处理任意的分布
- KF不太行,因为其噪声要求是高斯的,而且不自适应
理解此论文的内容需要有一定的理论储备。
3.1 Error Entropy & Kernel
3.1.1 简单介绍
这篇论文[3]详细地介绍了MEE的思想以及其与M-estimation的关系,我结合这篇论文简单说一下吧(这篇论文做的modification就不说了)。
此处使用的Entropy有别于通常说的香农熵(Shannon),这个熵被称为Renyi entropy,与香农熵的区别如下: \[ \begin{align} & H_s(X)=-\sum\log(P_i(x))P_i(x)\label{shannon} \\ & H_a(X)=\frac{1}{1-a}\log(\sum P^a(x))\label{renyi} \end{align} \] 公式\(\eqref{shannon}\)是香农熵,而公式\(\eqref{renyi}\)是Renyi熵。这两个式子让我想到了在DIP课上学到的两个滤波器,一个是普通的均值滤波器,另一个则是逆谐波均值滤波器(阶数可变那种)。香农熵就是Renyi熵在a趋近于1的一个特例。MEE中常用的是a=2(称为quadratic Renyi entropy)。论文[3]做作者提到的EE做的事实际上是:
The concept of ‘close’, implicitly or explicitly employs a distance function or similarity measure.
也即,EE定义的是一种相似 / 接近的度量。而由于EE在计算时引入了概率,普通的误差(或者说是偏差)是没有概率的归一、范围性质的,不能直接参与运算。核函数就起到了一个映射为概率的作用,我们可以理解为这是一个sigmoid / softmax: \[ \begin{align} & H_2(e)=-\log V(e) \label{h2}\\ & V(e)=\frac 1 {L^2} \sum_{j=1}^N\sum_{i=1}^Nk_{\sigma}(e_i-e_j) \label{kernel}\\ & k_{\sigma}(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{x^2}{2\sigma^2}\right) \end{align} \] 最后的Renyi EE就如公式\(\eqref{h2}\)所定义。最小化Renyi EE就是要最大化公式\(\eqref{kernel}\)定义的\(V(e)\),也即误差的QIP(quadratic information potential)。KF本质求解的加权最小二乘问题,ARKF为自适应加权鲁棒最小二乘问题。而其中的e,以我个人对论文的理解,应该表示的是新息。但是论文[2]里面实际说的是,\(e\)是滤波器输出与“期望输出”的偏差。嗯?期望输出是什么东西?其实是最优滤波器的输出,\(e\)是最优滤波器与当前参数滤波器输出的差异。
所以可以知道:
MEE准则是在优化最优滤波器和当前参数滤波器输出之间误差的误差熵。
然后我发现了有趣的东西:论文[4]是人机所老师们的文章,完全介绍了MEE-KF。而论文[2]对MEE-KF的介绍并不透彻,甚至看完之后我还不是很清楚如何实现。论文[4]则说得将一些细节说的更加清楚。
3.1.2 Parzen窗与Renyi Entropy
没想到还能和Parzen窗联系起来,当时没往这方面想。Parzen窗是一种核密度估计方法(非参数地估计概率密度函数,在我大三下学期的《模式识别与机器学习》课程中学了)。实际上公式\(\eqref{kernel}\)定义的就是一个Parzen窗操作,怎么理解?
- 首先,进行Renyi entropy计算需要计算IP(information potential)
- IP的计算需要依赖概率密度函数,这可以用Parzen窗估计出来
首先,Parzen窗法是这样的: \[
\begin{equation}\label{parzen}
\hat{p}(x)=\frac 1N \sum_{i=1}^N G_{\sigma}(x-e_i)
\end{equation}
\] 相当于在一堆\(\{e_i\}\)(已经采样得到的error)上放一个Gauss分布函数,再进行归一化,得到密度估计。通过采样得到的\(\{e_i\}\)可以估计出error的分布,从而计算信息势\(V_a(e)\)。二阶离散情况下计算为: \[
\begin{equation}\label{potential}
\hat{V}_2(e)=\frac 1N \sum_{i=1}^N\hat{p}(e_i)=\frac 1{N^2} \sum_{i=1}^N
\sum_{j=1}^N G_{\sigma}(e_i-e_j)
\end{equation}
\] 但上述公式还存在一些奇怪的地方,比如说\(\hat{V}_2(e)=\frac 1N
\sum_{i=1}^N\hat{p}(e_i)\)。明明正常情况下,二阶信息势应该是:
\[
\begin{equation}\label{v2}
V_2(x)=\int p^2(x)dx\rightarrow\sum_{i=1}^N p^2(x)
\end{equation}
\] 此处直接把二次项去掉了,相当于对\(p(x)\)按其自身的加权平均变成了直接平均。可能是一种近似计算方法吧,因为平方确实会麻烦一些,将会写成以下形式:
\[
\begin{equation}\label{right}
V_2(x)=\sum_{i=1}^N p^2(x)=\frac 1{N^2}\sum_{i=1}^N
\left(\sum_{j=1}^NG_{\sigma}(e_i-e_j)\right)
\left(\sum_{j=1}^NG_{\sigma}(e_i-e_j)\right)
\end{equation}
\] 这显然是与公式\(\eqref{potential}\)有一定差别的。相当于公式\(\eqref{right}\)是将其中一个内求和式近似为了1(这合理吗?虽然论文说的就是:one can obtain an estimate of the second order (α = 2) information potential),感觉Parzen窗(一次近似)+
均匀分布(第二次近似)是两次近似啊?还是我理解错了?但是确实这样的近似会让Renyi
Entropy更方便计算。之后的推导就非常复杂了。之后开单独的一篇进行分析,我可能自己也会尝试实现一下,既然有闭式解那么可能实现起来并不会太复杂吧(?飘了)。
3.2 约束与闭式解
说实在的,我觉得这个略有点“强行创新”的感觉。不知道怎么说这个比较好,可能是我太菜了没看明白。论文[2]做的事情是增加了一个约束(还是等式约束): \[ \begin{equation}\label{const} \mathop{\arg\max}_{\pmb{w}}\hat{V}_2(e_n)\text{ subject to }\mathbf{C}^T\pmb{w}_n=\mathbf{f} \end{equation} \] 后面这个约束是用来干什么的呢?什么实际问题下会有这样的约束呢?就抓住这样一点小的改动就可以有一篇论文嘛?虽然后序的推导还是很有意思的,作者通过约束 + 变换求出了对应的拉格朗日乘子的取值。其中需要设置的是约束参数\(\mathbf{C}\)以及\(\mathbf{f}\)。
仔细一看,还是我们学校的老师(陈霸东教授)作为其中一位作者。当然也有可能是因为,论文长度只有5页(因为是篇brief),有些推导不是特别的详细。但可能我还是觉得,就多讨论了一个约束的情况,没什么太大的意思吧。
IV. ESKF
我在做机队的某项定位任务的时候用到了ESKF(Error-State KF)[5],对机器人的轮速 / IMU / UWB(定位信号)进行融合。ESKF与普通KF最根本的区别在于:
- 普通KF的状态就是可以直接使用的,具有明确物理含义的状态,比如速度 / 位置 / 角度。
- ESKF的状态是误差,状态转移 / 观测都是有关误差的(比如位置误差 / 速度误差),相当于是一个对误差进行滤波得到结果,每次使用滤波估计出的系统误差进行原状态的计算。
- 可以理解为:KF是位置式的控制(每次滤波得到的都是最终结果),而ESKF都是增量式的控制(每次滤波得到的是状态应有的变化值)。
状态总是由两部分组成:实际状态(true state)= 理想状态(nominal state)+ 噪声状态(error state)
KF对实际状态进行滤波,ESKF对噪声状态进行滤波,而理想状态进行无误差假设,直接更新。关于ESKF的使用,这里就不赘述了,因为我也赘述不出来:
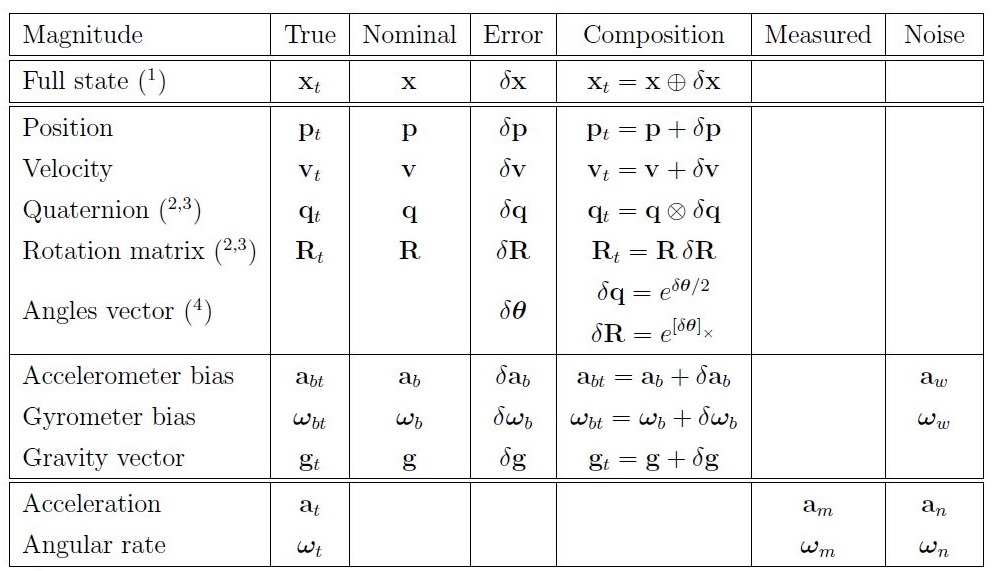
涉及到大量的四元数 / 运动学 / 机器人学知识,常用于定位,因为它有很显著的优点:
- error-state很小(因为是误差),相当于使用相对量进行计算,一般不会出现奇异 / 万向锁之类的问题。
- 另一方面,由于其很小(一般都在0附近,并且范围不太大),对于复杂的运动学问题(特别是非线性系统),Taylor展开后高阶项一般都是可以忽略的,性质很好。
Reference
[1] Durovic Z M, Kovacevic B D. Robust estimation with unknown noise statistics[J]. IEEE Transactions on Automatic Control, 1999, 44(6): 1292-1296.
[2] Peng S, Ser W, Chen B, et al. Robust constrained adaptive filtering under minimum error entropy criterion[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 65(8): 1119-1123.
[3] Liu W, Pokharel P P, Principe J C. Error entropy, correntropy and m-estimation[C]//2006 16th IEEE Signal Processing Society Workshop on Machine Learning for Signal Processing. IEEE, 2006: 179-184.
[4] Chen B, Dang L, Gu Y, et al. Minimum error entropy Kalman filter[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019.
[5] Sola J. Quaternion kinematics for the error-state Kalman filter[J]. arXiv preprint arXiv:1711.02508, 2017.