关于变形金刚的一些思考
Transformer
I. 引入
在NLP(Natural Language Processing 而不是 Non-Linear Programming)问题中,经常涉及到sequence to sequence的问题,在这种问题上最广为人知的应用就是【机器翻译】:
Watch out everybody, the potato is really hot. Nice.
大家快看外面有一个特别性感的土豆。好棒啊。
而RNN及其变体如GRU/LSTM,既然属于RNN范畴,那就免不了串行以及自递归(auto-regression)。在数字信号处理课程中学的知识:自递归对应了IIR,时域上比FIR复杂一些。由于这两个显著的弱点,导致其慢并且长距离下的语义解析能力差,Vaswani等人提出了一种新的 基于注意力机制的可并行处理框架 - the 变形金刚。在此基础上,Juho-Lee等人构建了一种对集合数据具有置换不变性的网络(集合无序,输入顺序不影响输出)。因为从小就是看变形金刚系列电影长大的(?),我实现了这两篇论文中提到的神经网络结构,用在了Set Transformer论文中的Toy Problem - Max regression 上。结果如下图,本文是对Transformer相关理论以及实现的总结,实现已经挂在Github上了,见Github🔗:Enigmatisms/Set-Transformer。
II. Attention机制的理解
2.1 与RNN的关系
RNN中的典型结构(我也不记得叫什么了),总之是一个有记忆能力的Gate。神经元的上一个输出,可以作为本次输入的一部分,那么这可以被简单地表示成: \[ \begin{equation}\label{rnn} y[n]=a\times h[n]+b\times x[n],\text{ where }h[n]=y[n-1] \end{equation} \] 显然,一个简单的记忆单元可以被表示成一个离散一阶系统,那就是一个惯性环节嘛。这也就是一个自递归单元。很可惜,这样的系统阶数越高,表示力才越强,但作为代价的是,需要系统提供存储单元,并且对于一个k阶系统,前k个值如果没有完全计算完成,那么第k+1个值是无法得到的,这也就阻止了并行,这太不优雅了,虽然可能 一定程度上模仿了人类的理解方式:顺序读,再处理顺序输入的信息。
我个人不是很了解RNN,因为个人觉得这个网络结构就是不是特别优雅(虽然看起来很有道理),加上我偏CV,一般也用不到RNN。我在想,RNN能做到以下的事情吗?
另外,在常规接当种中我也们发现,免疫相对功能较低人的群,以及60岁上以的人群,他们接踵产生后的免效疫没有果18-59岁的好,但是这类人群又是恰恰感的染后高危人群
上面这段话的内容,存在一些颠倒的字词,人可能没有太大的阅读障碍,但是依赖顺序输入的网络表现会如何?
与之相比,Transformer是一种FIR,它无需依赖记忆单元,在输入时也没有顺序要求(Attention is All You Need一文中使用三角函数Position encoding),于是可以很方便地进行并行。并且Transformer使用的注意力机制,就是模仿人类理解信息时,有所侧重的特性。
2.2 单头细节
Query,Key,Value(Q K V)的物理含义应该如何理解?假设问题的背景是机器翻译,那么有两种情况:
- Q是输入语言,(K,V)是目标语言对应的信息。输入的每一个token,变为Q之后查应该对应目标语言中的哪一个词。
- Q是目标语言,(K,V)是输入语言信息。目标语言查自己应该如何选择目标token才能使得最类似输入
个人认为在Transformer中,应该是用第一种方式来处理问题。那么Q,K,V在其中的作用个人认为分别是:
- Q:输入embedding信息,用于与目标语言的信息进行比较
- K:目标语言构建的,方便源语言(Q)进行比较的,包含目标embedding信息的张量
- V:用于输出的目标embedding信息部分
考虑batch的情况下,一般的张量shape(以Q为例),大概是这样的:\((N_{\text{batch}},M_{\text{seq-len}},K_{\text{embedding-dim}})\)。也就是,三维张量已经足够表示:batch size,序列长度,以及embedding维度。有的时候,Q与K的shape会相同,以下以QK处于同一个线性空间为例,那么Q/K所在的空间内可以形成Gram矩阵:
在线性代数中,内积空间中一族向量的格拉姆矩阵(Gramian matrix 或 Gram matrix, Gramian)是内积的对称矩阵,其元素由\(G_{ij}=(v_j|v_i)\)给出。
之前在CNN style transfer中接触过,这个矩阵用于衡量两组向量的相似程度。因为内积可以用于衡量相似度。使用内积就会有一种使用agreement概念的感觉。最后的输出是: \[ \begin{equation}\label{qkv} Att(Q,K,V,\omega)=\omega(\frac{QK^T}{\sqrt{k}})V \end{equation} \] \(QK^T\)就是Gram矩阵,要注意KV的对应性。可以这么说:假如\(Q_i\)与\(K_j\)的相似度高,那么\(V_j\)应该有更大的权值。\(\omega\)是非线性函数,论文中使用的是softmax,变换为多元素的概率,进行概率加权。
Softmax沿着哪一个维度做?已知QK的计算是:\(QK^T\)也就是\((n\times k)\times(k\times n)\),最后生成\((n\times n)\)矩阵
每一个Query token与key匹配的关系有两个选择:
- 一个query可以选择多个key,也就是选择不同key的概率是归一的,那么就是行和为一()
- 一个key对应了多个query,那么就是列和为1(列方向求和)(这个在2.2节开头就已经说过了,属于方式2,应该是不对的)。
个人更加倾向于,一个query可以对应多个key,也就是一个query可以找到多个value?也就是每一个query字,与所有value字的注意力,对应的概率应该和为1。
2.3 单头理解 & 多头化
| 单头QKV注意力块 | 多头QKV注意力块 |
单头QKV可以理解成:源数据经过特征提取得到Q,目标空间由V对应的元素展成(span),并且提供一个与Q中元素相同维度的比较信息(K)。源信息(Q)与部分目标信息(K)元素两两求相似,通过相似度转化为的概率对V进行加权输出。
多头则是指:Q K V并不直接进行内积运算。一是因为可能是大矩阵,直接内积计算时间长,二是因为这样学习得出的内容太单一。多头注意力就是希望通过多重低维度映射的方法,使得不同的head能够学习到不同的源 / 目的数据关系,这是产生多重语义理解的一步。
III. Set Transformer
3.1 Inducing Point & ISAB
ISAB中的Inducing Points与PMA中的seeds实际上是一回事,叫法不同。从论文中摘录的框图说明了ISAB的实现结构。它的提出是为了解决SAB平方复杂度导致的问题。比如当集合特别大的时候,会因为平方级别的复杂度计算很长时间。
SAB的时间复杂度为什么是\(O(n^2)\)?SAB作为自注意力网络块,Multi-head attention输入的Q K V都是X,也就是说:对于一个输入X,不考虑其batch大小,假设其为(\(n\times k\)),n为集合大小(或者在NLP中,token的数量),k为embedding的大小。那么根据内积: \[ \begin{equation}\label{self_att} Att(X,X,X,\omega)=\omega(\frac{XX^T}{\sqrt{k}})X \end{equation} \] 过程大概是:\((n\times k)\times(k\times n)\times(n\times k)\)。第一个QK阶段就已经需要n平方次计算了。这个就是\(O(n^2)\)复杂度的。所以作者希望,可以固定某一维度的大小,以降低复杂度。
MAB是\(Att(X,Y,Y,\omega)\)形式的,那么当MAB的输入是:\((I,X,X)\),最终的计算会成为:\((m\times k)\times(k\times n)\times(n\times k)\)。在QK阶段,内积运算只进行\((mn)\)次,复杂度是\(O(mn)\),当输入为大集合时,可能可以显著减小计算负担。所以两层MAB的交替输入,第一层输出\((m\times k)\)作为第二层MAB的Y,X本身作为第二层的X,可以最后重新映射回到\((n\times k)\)维度。
作者自己也说(我觉得作者这个类比很不错,很直观),ISAB就像一个编码器,或者说常见的Detection / Segmentation的两头大中间小结构:
This is analogous to low-rank projection or autoencoder models, where inputs (X) are first projected onto a low-dimensional object (H) and then reconstructed to produce outputs.
3.2 实现细节:维度?
开始时,我实现了一版这一样的MAB,请看:
1 | class MAB(nn.Module): |
Multihead这个模块就是根据Attention is All You Need这篇文章来的(至少我觉得我是这么实现的)。但是发现,这没办法实现维度变换。为什么?我发现我在解决中位数问题时,遇到了这样的难题:
- 一个训练用例,显然是\(\{x_1,x_2,...,x_n\}\),x是标量,使用SAB时,内积还是标量,用处不大。
- 低维数据能向高维转移吗?自己实现的这一版SAB,输出就是:(batch_size, token_num_Q, embedding_dim_V),如果内部不对数据做变换,那么输出的embedding维度就是1
不管是在Transformer论文还是在Set Transformer论文中,提到Multi-head一定做的是这个事情:首先将Q K V变换到低维度上(以Q为例) \[ \begin{equation} Q_i=QW_q^i,\text{ where } W_q^i\text{ has shape }(N_{batch},d_q,d_q/M) \end{equation} \] 将变换后的Q K V输入到single-head attention模块中。巧了,我就是这么做的,只不过感觉会引起维度问题。所以我们需要:
- 可以设置输入输出维度(设置输出维度极为重要,就像我们用CNN输出多少个Channel一样,应该是可调的)
- 输入时对较小的维度进行升维,以便进行Multi-head操作、
所以Transformer在实现时,到底应该如何操作?Q K V看起来很简单的三个维度设置,需要统一维度吗?
个人认为,在Set transformer中,多头注意力机制模块应当完全不需要对输入进行变换,直接使用。这样才可以模块独立。而不同的Block之间的连接,有赖于Feed forward层,或者说,有些Block的输出(比如MAB),就会经过FFN。
row-wise feed forward 层,一般来说也就是一个单层的线性网络(不过要记得激活,开始时忘记加ReLU了,既然是层,那就要有激活,除非是输出)。可以认为,此处就是一个类似残差块的东西。虽然在Attention is All You Need中,FFN是这样定义的: \[ \text{FFN}(x)=\max(0,xW_1+b_1)W_2+b_2 \] 相当于nn.Linear + nn.ReLU + nn.Linear。但是在Set transformer中,实现的貌似叫做 row-wise(all you need中叫做position-wise)。但是为什么要这么做?作者没有给出明确的答案,而是说:
It could reduce to applying a residual block on X. In practice, it learns more complicated functions due to linear projections of X inside attention heads.
感觉挺无力的,这些深度学习新的网络架构看起来好像确实没什么可以解释的,数学上也不好说。残差连接在这似乎也与其被提出时所要解决的问题对应的目的不同,因为不会有什么梯度爆炸。
3.3 多头注意力的实现
多头注意力是我在本文中最觉得困惑的部分。因为官方的实现与自己的论文 / All you need是不一样的。不管是在Transformer 还是 Set Transformer论文中,提到的多头的实现方式时,总会将以下公式列出来: \[ \begin{align} &\text{output}=\text{cat}[O_1,O_2,...,O_h]\cdot W_o,\text{ where }O_i \label{out}\\ &O_i=Att(Q_i,K_i,V_i,w)\\ &Q_i=QW_Q^i,K_i=KW_K^i,V_i=VW_V^i, \end{align} \] 也就是:对Q K V 每一项分别使用多个权重\(W\),从原来的embedding dimension k映射到一个更低的维度(实现低维多输入,低维上的注意力)。公式\(\eqref{out}\)是两篇论文中都有的,但是作者并没有这样实现。作者直接使用了split(fron Github juho-lee/set_transformer)
1 | Q_ = torch.cat(Q.split(dim_split, 2), 0) |
相当于,本来应该使用线性映射到低维的Q K V,直接在embedding dimension维度切开,成为head number份。这和你的论文里写的也不一样啊,为什么呀大哥。此后,官方实现有些更迷惑的操作:
1 | A = torch.softmax(Q_.bmm(K_.transpose(1,2))/math.sqrt(self.dim_V), 2) |
连起来就是:首先embedding直接split成块,拼接到第一个维度上(一般来说是batch维度),相当于原来batch size为n现在变成了\(h\times n\),batch之间不会有相互作用。计算内积之后,再拆分回到原来的shape。所以我也不是很懂为什么不按部就班实现。。。可能这就是强者吧。我的实现,只能说按着论文来的:
1 | Qs = Q.split(self.dk, dim = -1) |
split本质上与线性映射没有什么区别,甚至split实现会简单很多,并且少一些参数。
IV. 复现结果
- 学习率设置
4.1 学习率
测试的问题是Set Transformer中的Max Regression问题,找一个集合的最大数,本来想实现中位数的,但是发现中位数简直没办法直接训练出东西来。训练参数:batch size = 64,一个集合32个数,也就是每次的X是\(64 \times 32\)矩阵。模型非常难训练,主要体现在:
我使用exponential learning rate scheduler,初始学习率1e-3,gamma大概为0.9999(衰减慢),正常情况下,在初始的几百个样本,loss下降非常快。到loss约等于2时,可能一直卡在这直到结束,最后的acc也就20%。
有很小的概率,学习率减到很小时,跳出局部最优解。acc继续上升,但是由于ExpoLR让学习率变得很小了,训练很慢,训练完也只能让模型acc到50%。
官方实现可以在较大学习率时跳出局部最优。所以最后学得很快,训练结束时到了90%。
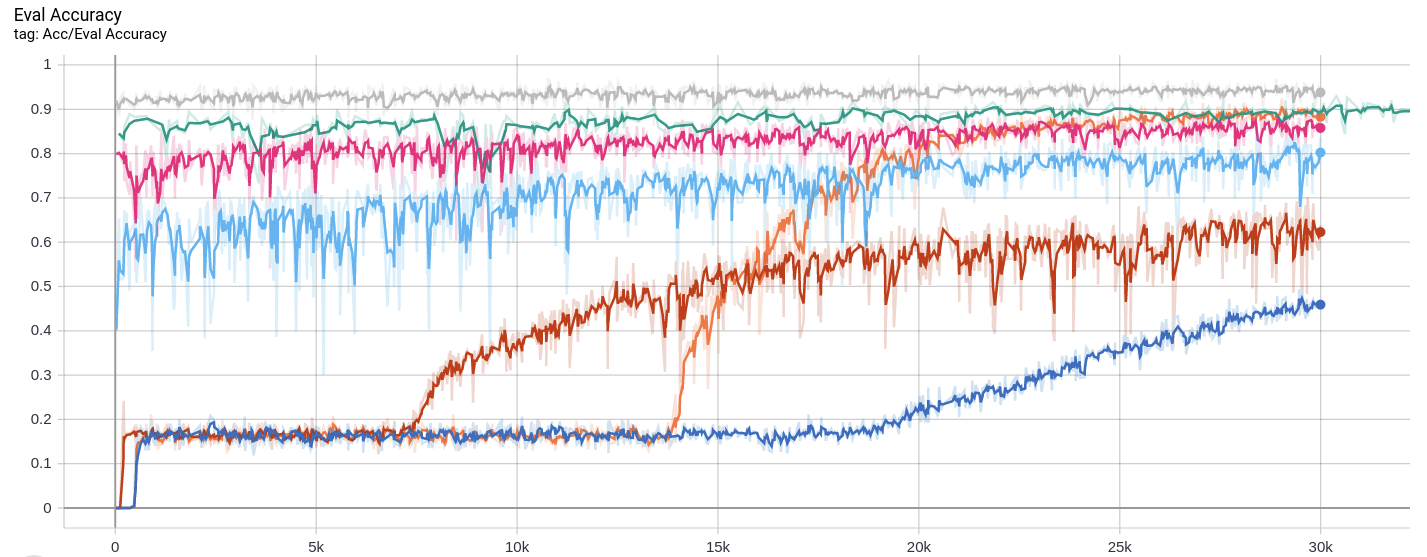
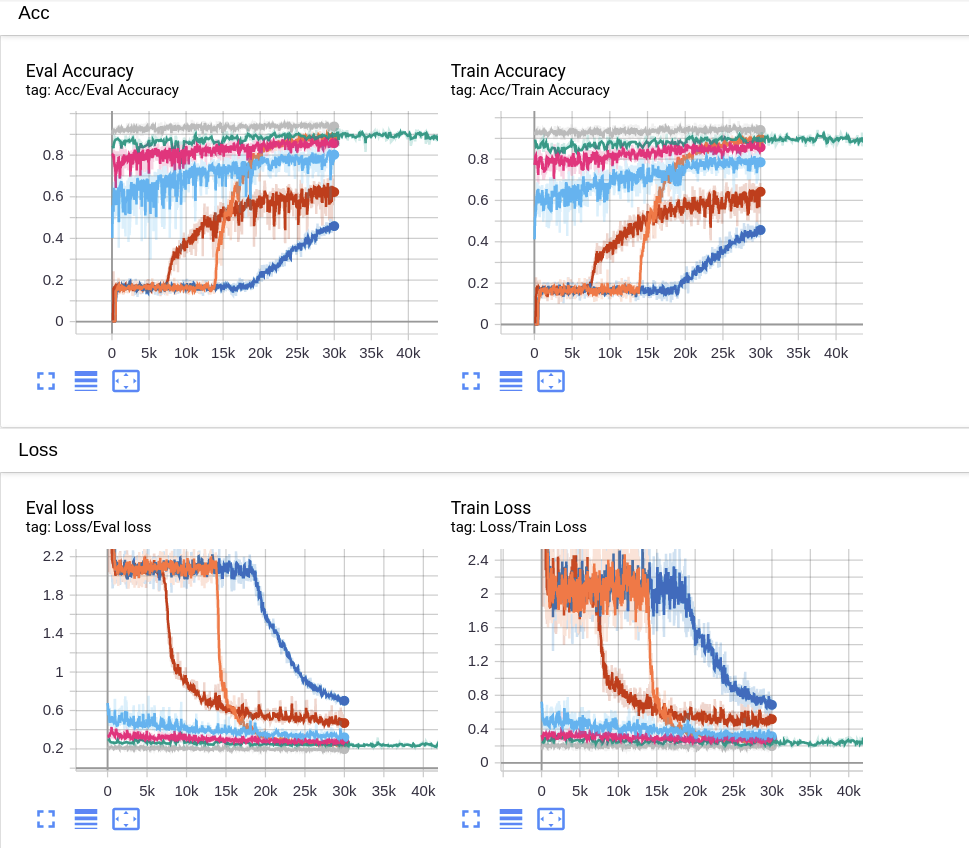
上图中,在15k个epoch突然飙起来的橙色曲线是官方实现思路的MAB,很快就收敛了。深蓝色曲线则是我说的那个exponential LR训练结果。
之后我换成Multi Step LR,开始200个epoch学习率很大,loss下降很快,[200,1000]内的学习率是上一阶段的1/10,此后则是1/100。看起来真的是学习率过大。此后其他的曲线都是学习率精调得到的结果。
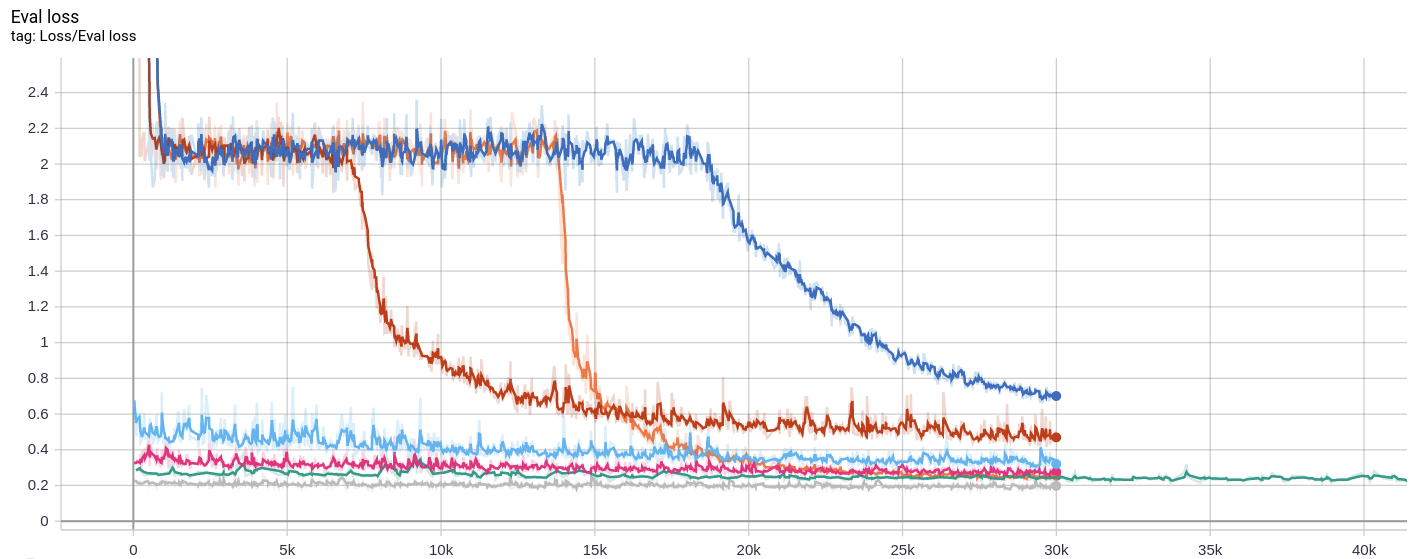
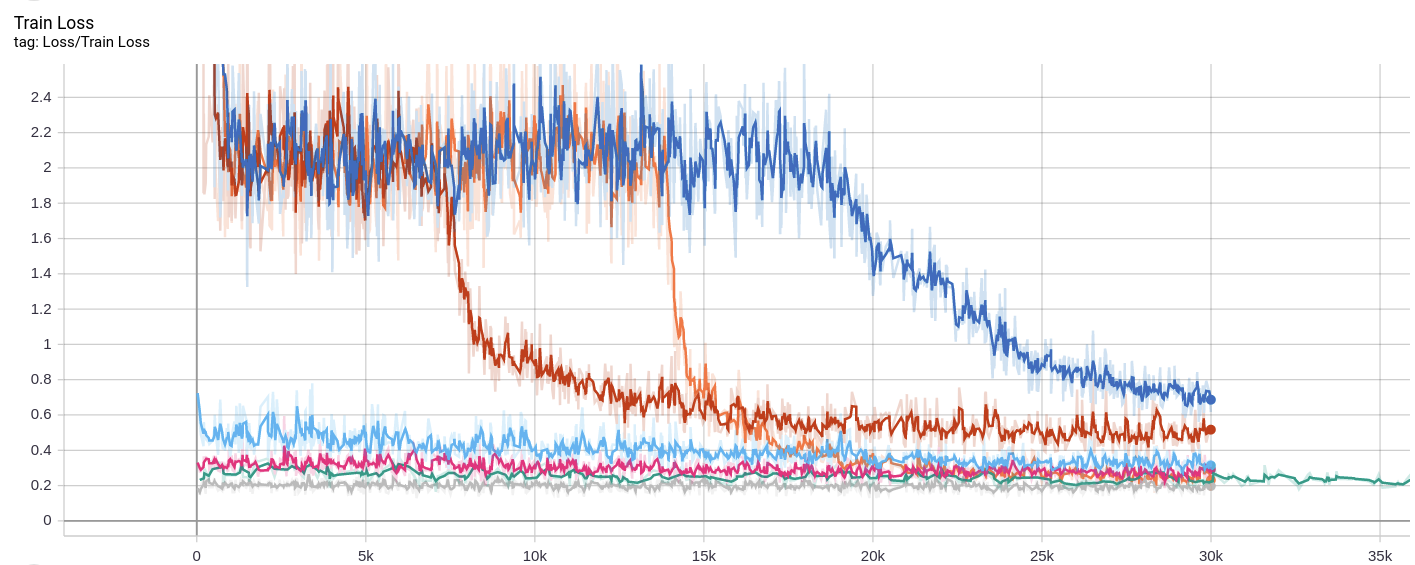
可以看到,灰色的曲线是最后一次的训练结果。也就是说,我的实现比官方实现训练次数多了好几倍,达到的acc之比官方高了个4%。
V. Funny Thing about Transformer
谁让Vaswani起了一个倍具争议的名字呢?
实名赞同楼上:
赞同,但是我要提方案:
我有些疑问:
实名反对楼主:
反对反对(nm啊,这名字真的很踢馆)
我来折衷:
注意力?小马宝莉(My Little Pony简称MLP)最强:
你们搞NLP的还挺有意思的。