骷髅融合者-CVPR2021

Posted on Edited on In Views: Symbols count in article: 3.5k Reading time ≈ 3 mins.

骷髅融合者

I. Intros

​ 想看看CVPR2021上都有关于点云配准或者点云处理都有什么样的文章，网上搜刮了几篇，骷髅融合者就是其中一篇。这篇论文的作者貌似是上海交大的本科生，嗯 本科CVPR一作，卢策吾老师团队，可以说是很nb了。本论文提出的思想，个人认为比较简单（可能是因为比较复杂的部分被PointNet++掩盖了，文中也没有使用时下最为流行的【变形金刚】）。并且看完Introduction之后，我就觉得这个思想好像在哪里见过：嗷，原来是我的灯条检测中含有这个方法的弱弱化版。

​ 本短篇博客只做该论文的一个简单分析，并不附带复现（如果要带复现的话，一是需要时间，二是需要了解PointNet++）。论文的地址是：arXiv: Skeleton Merger: an Unsupervised Aligned Keypoint Detector

Figure 1. Skeleton Merger 论文效果

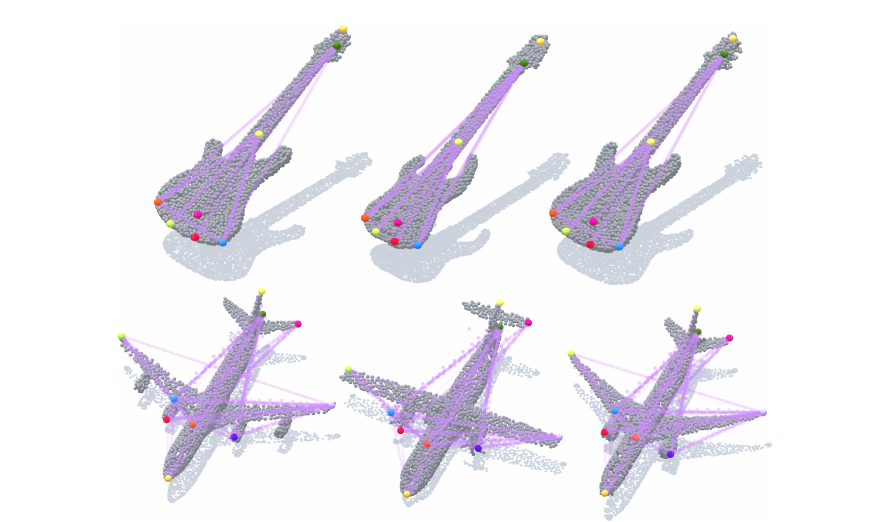
II. 论文思想

2.1 思想概述

Figure 2. Skeleton Merger 论文思想框架

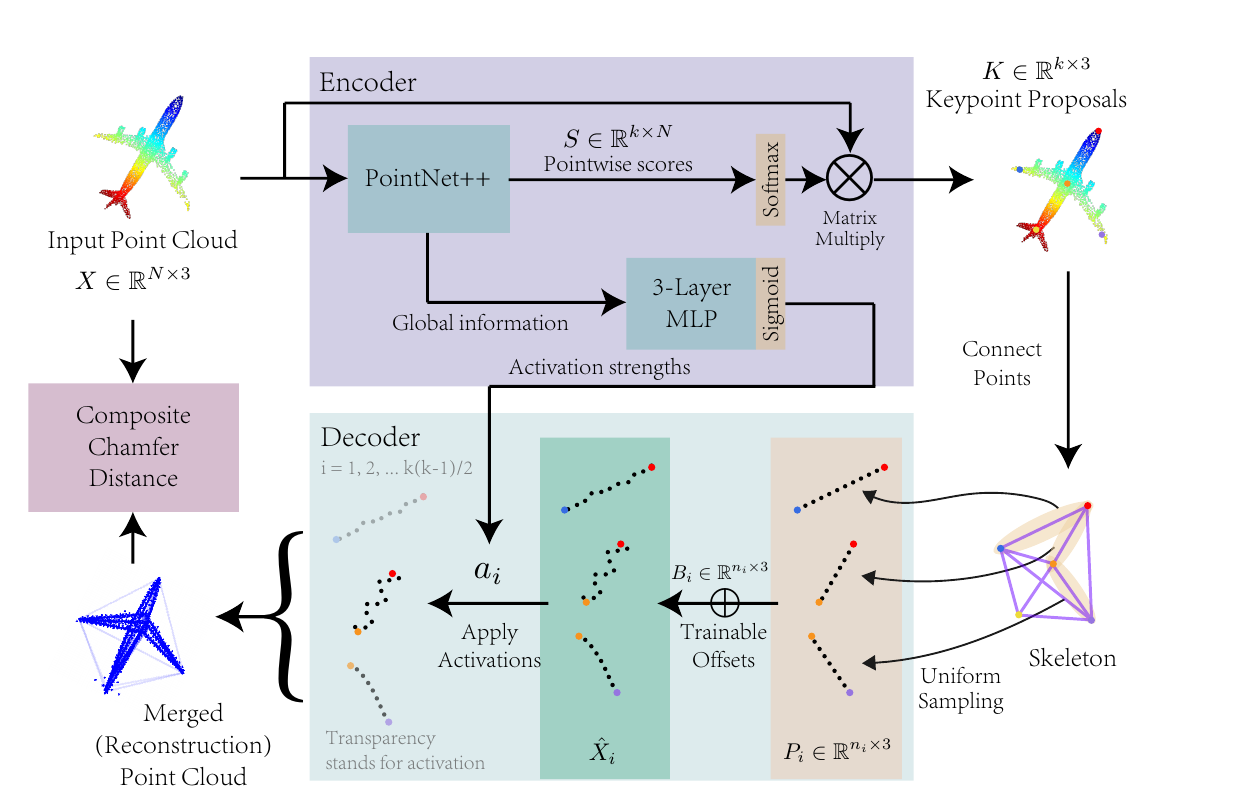
​ 作者使用了一种“重构误差”的思想，使用一个更简单的表征，来重构一个点云，使得原始点云与生成的点云在某个metric下最为相似。而我在RM时做的工作：无监督优化算法的灯条检测，也是类似：

  • 找两个key points（灯条的端点），使用灯条的端点根据hand-crafted重构方法，重构出灯条，使得生成的灯条与原始灯条图像的L2差距最小。（所以可以说，我大二下学期写的这个算法是本论文的弱弱化）

​ 本文的思想大概可以被总结如下：

使用PointNet++，生成一个加权矩阵，加权后可以生成k个key points，同时，PointNet++也会输出一些全局信息。生成的key points自然形成一个完全图。

使用PointNet++输出的全局信息，过3层MLP，生成【activation strength】，此后我们会知道，这实际就是skeleton完全图中，每条边存在的概率。

完全图上，每条边都可以产生一个sub-cloud（均匀采样得到，点数与长度成正比）。之后通过一个网络（decoder），学习每一个点的offset（相对于骨架的移动），使得生成的点云可以表征更加复杂的形状。

使用Composite Chamfer Distance（CCD，一种改进的Chamfer Distance方法）作为loss函数，使得原始点云与生成点云的CCD最小【无监督模型的生成式loss】。

​ 本文不涉及任何网络结构以及网络设计，只是分析一下：

  • 其方法有哪些亮点
  • 个人认为其方法可能存在哪些不足

2.2 亮点

​ 本人认为，此论文突出的两个亮点就是：

  • skeleton重构误差
  • CCD误差函数的设计

​ 首先，通过skeleton重建点云，来辅助判定key points的选取效果，可以使得其达到无监督的目的。在MoCo论文分析中，实际上已经说过，无监督的loss也就主要是那么两种（据我目前所知的“主要”）：

  • 对比loss（以MoCo为代表的），主动生成匹配与不匹配的样本，最大化不同类别特征之间的差别
  • 生成式loss（autoencoder思想），主要思想是：学出来的特征能够经过某种方式重构输入，特征学得越好，从直觉上来说，重构效果越好。

​ 第二种方法的显著问题就是：一般会有比较大的计算开销（特别是重构图像时，长采样、反卷积结构等等）。个人感觉，本文是一种生成式的loss，但是由于：（1）key points（对应的边）具有稀疏性（2）均匀采样密度可控性，计算开销可能不会太难以接受。

​ 本文直接对key points形成的完全图进行重构，生成一个个的sub-cloud，但是由于有些边采样出的点，实际是不存在的，应该在其存在性上就予以抹杀（而非在offset学习阶段，强行将其拉回到某个位置），故作者引入了activation strength，每条边都将有一个对应的activation strength，相当于是边权，边权小的边对应的生成点在reconstruction过程中可能被丢弃，并且在loss计算过程中，也可能不会参与。

​ 此外就是CCD误差函数的设计。CCD是Chamfer distance的一个扩展，Chamfer distance可以简单地将其理解成：最邻近点距离。在一个n维metric space中给定两个集合A，B，（比如）A中的某个点\(p_i\)到B中的最近点的距离，就是Chamfer distance。

​ 在本问题中，集合A、B分别是生成点云与原始点云。但是需要注意，Chamfer distance是单向的，那么需不需要构建成双向对称的loss函数呢？答案是否定的，本问题本身就不是一个对称的问题。作者做了一个分类：

对每一个生成点云中的点\(p_i\)，计算\(p_i\)在原始点云中的最近点\(q_i\)，并且计算对应的Chamfer distance，使之最小化，这是在提升生成点云的fidelity（准确性），也就是说：生成点云的“大致形状”应该与原始点云类似。

对每一个原始点云中的点\(q_j\)，计算\(q_j\)在生成点云中的最近点\(p_j\)。这就是不对称性的体现：即便生成点云每个点在原始点云上都有很好的对应点，由于生成点云可能具有稀疏性，反过来，原始点云的某些点可能没有办法在生成点云上找到很好的对应点。数学上来说，这就是：单射和满射。正向loss如果很小，只能保证生成点云的fidelity问题，能建立一个很好的 生成点云\(\rightarrow\)原始点云的单射，但是反过来，如果原始点云的每个点也能在生成点云上有很好的对应，那么可能可以建立一个原始点云\(\rightarrow\)生成点云的单射，使得 coverage问题得到解决。

​ 正向fidelity loss很简单，就是这样： \[ \begin{equation}\label{fid} L_f=\sum_k a_k\sum_i\Vert p_i-q_i\Vert^2,q_i=\mathop{\arg\min}_{q}\Vert p_i-q_i\Vert \end{equation} \] ​ 而反向coverage loss就没有那么简单了。首先，加入反向loss也如上式一样，定义成对称的，那么最终结果将会是：我直接让所有\(a_i\)训练成0得了，没有点存在，就没有loss！显然这是很有问题的。

​ 一方面，我们希望\(a_i\) (activation strength)可以起到作用，另一方面我们又希望避免上述问题，我们也希望不会因为公式\(\eqref{fid}\)内部的\(a_i\)存在，使得\(a_i\)倾向于变小。作者提出了两个策略：

  • 为了体现“coverage”，作者将会【一配多】，也就是说，不再寻找距离最小的一个点，而是：查到点\(q_i\)后，删除\(q_i\)来源的那条边（以及所有点），并且累加本边对应的activation strength到一个本地的（初始化为0的累加器）变量w上。如果w小于1，那就继续在剩余点中查找最小距离点，重复上述操作，直到w>1或者没有客用边。
  • 假设已经没有可用边了，而w<1，则进行惩罚（说明我们让\(a_i\)学得太小了），在loss上增加\(\gamma (1-w)\)，论文中\(\gamma\)选取20.0，比较大。

​ 上述操作可以保证：\(a_i\)不会因为优化CCD而变得很小。

2.3 个人觉得存在的问题

2.3.1 稀疏性问题

​ 作者如何重建其生成点云的呢？首先：根据图结构，每条边进行均匀采样。每条线段上有若干个点。此后使用一个网络进行offset学习。这样会存在一定问题：重建的点云可能就是很稀疏，导致CCD coverage loss计算总是比较大。比如：一个圆柱型的物体，在同一高度上，绕轴不同角度可能存在很多个点，但对于本论文的方法，一个高度上就一个点，那么对于圆柱型物体，只能使用螺旋式的offset，这会使得某些位置上比较稀疏。

​ 要解决这个问题，可能可以在初始时同一个位置采样很多个点，之后使得这些点，在过本点，垂直图结构边的平面上扩散开来。我认为这样的话，学习的参数可以减少（每个点只需要学习一个参数而不是三个），也可以解决稀疏问题。

2.3.2 最邻近搜索

​ 这只说下我的担忧：最邻近搜索快速吗？当然，可以使用一些加速的数据结构，比如8叉树，KD树等等，但是能有多快呢？不好说，我没有做过实验，但是这也就是非完全的生成式loss遇到的问题，loss构建时的稀疏性问题。所以个人认为，此处可以将最邻近loss换为别的loss。