位姿变换与六轴仿真

Posted on 2021-10-31 Edited on 2021-11-01 In learning Views: 372 Symbols count in article: 10k Reading time ≈ 9 mins.

Axis6

稚晖君牛逼。看了他的六轴机器人之后，我感觉自己没学过自动化。为了证明自己是自动化专业的学生，我尝试学习以及手推了一下正逆运动学公式，手写了一个六轴机器人的控制、仿真（rviz以及Gazebo: for those who doesn't know how to pronounce: ɡəˈziːboʊ，重音在前），代码放在了[Github🔗:Enigmatisms/Axis6]。本文包含如下内容：

位姿变换/正逆运动学的一些基本知识
Gazebo的配置使用
仿真效果视频（~~高清无码~~）

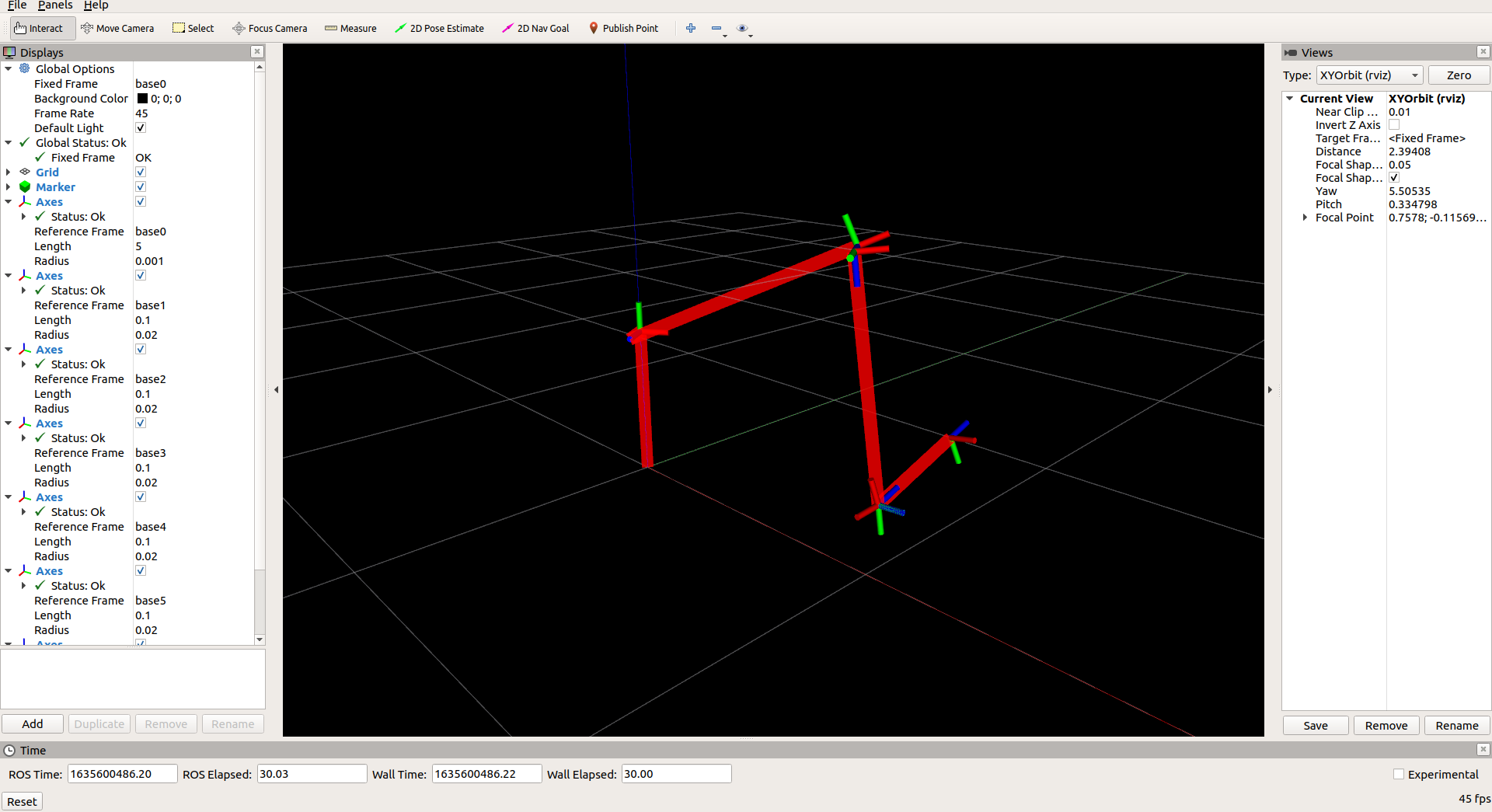
这里放两张图：


rviz仿真结果	Gazebo仿真结果

Figure 1. 仿真效果图

II. 前置知识

2.1 位姿变换左右乘

这个问题个人之前一直没有搞清楚，也没有静下心来推过。

给定空间中一个点p以及一个位姿变换 $T = [R t]$ （非齐次），点p经过位姿变换的结果应该是： $\begin{matrix} (1) & p^{'} = R p + t \end{matrix}$ 那么现在有这样一个问题，如果我想对点p进行多次变换？或者是进行一次两个位姿变换合成对应的变换？应该怎么做？假设我们有两个位姿变换： $T_{1} = [R_{1} t_{1}]$ 以及 $T_{2} = [R_{2} t_{2}]$ ，乍一看应该这么做： $\begin{matrix} (2) & p^{'} = R_{2} (R_{1} p + t_{1}) + t_{2} = R_{2} R_{1} p + R_{2} t_{1} + t_{2} \end{matrix}$ 上面这个公式，思想非常直白。不是要多次变换吗？不是要合成吗？那就直接先变换一次，再对结果变换一次就行了。但是实际上，对于位姿变换合成问题而言，这是错的结果。首先，我在这里给出结论： $\begin{aligned} (合成变换) & p^{'} = R_{1} (R_{2} p + t_{2}) + t_{1} = R_{1} R_{2} p + (R_{1} t_{2} + t_{1}) \\ (变换的复合) & p^{'} = R_{2} (R_{1} p + t_{1}) + t_{2} = R_{1} R_{2} p + R_{2} t_{1} + t_{2} \end{aligned}$

合成变换，与变换的复合是两回事。

很多时候，我们接触的都会是合成变换。举一个例子：点云配准。假设点云A到点云B的位姿变换为T（点云A对应的激光器坐标系需要经过变换T才能变换到点云B对应的激光器坐标系位置），已经存在一个粗糙的初始位姿变换： $T_{0}$ ，这个变换可以是里程计或者一些算法给出的，需要 精配准 来修正这个位姿变换，使之更符合实际观测，那么假设这个精配准模块求出，点云在位姿 $T_{0}$ 下，还需要进行的变换 $Δ T$ ，最后合成 $T_{0}$ 与 $Δ T$ 得到最终的变换。合成变换与变换复合的本质区别是：讨论的坐标系不同。变换的复合具有非常简单的思想，正如函数的复合，对输出进行一次新的变换。两次变换都是在同一个坐标系下讨论的，可以认为：

参与变换复合的两个变换，是两个互不相关的，在同一个坐标系下讨论的绝对位姿变换，之间没有相对性。

而合成变换，则具有相对性。仍然以上面的点云配准为例子， $Δ T$ 变换是在 $T_{0}$ 变换的基础上进行的，是在 $T_{0}$ 对应的坐标系下的一个变换，而 $T_{0}$ 是相对于另一个坐标系（比如全局坐标系或者子地图坐标系而言）。也就是说：

参与合成变换的两个变换，具有关联关系，其中的一个变换是基于另一个变换确定的坐标系来讨论的。

既然如此，那么在两种情况下的【合成的】变换分别是什么？ $\begin{aligned} (合成变换) & T = T_{1} T_{2} \\ (变换的复合) & T = T_{2} T_{1} \end{aligned}$ 只简单说一下合成变换为什么是右乘：显然，因为 $T_{2}$ 是在 $T_{1}$ 变换后的坐标系下的一个相对变换，其中的平移量相当于直接被 $T_{1}$ 预先变换了一次（平移就相当于是一个点）。整个式子可以看成是： $T_{2}$ 变换被 $T_{1}$ 预先变换了一次，由于是 $T_{1}$ 来变换（动词） $T_{2}$ ，则显然 $T_{1}$ 应该放在左边。

所以要回答左右乘问题，其中一个角度应该是：

左乘对应了绝对变换，右乘对应了追加变换，是在前一变换对应坐标系下讨论的。

2.2 左右乘讨论的衍生

为了方便理解，我画了一个图：

Figure 2. 位姿变换示意图

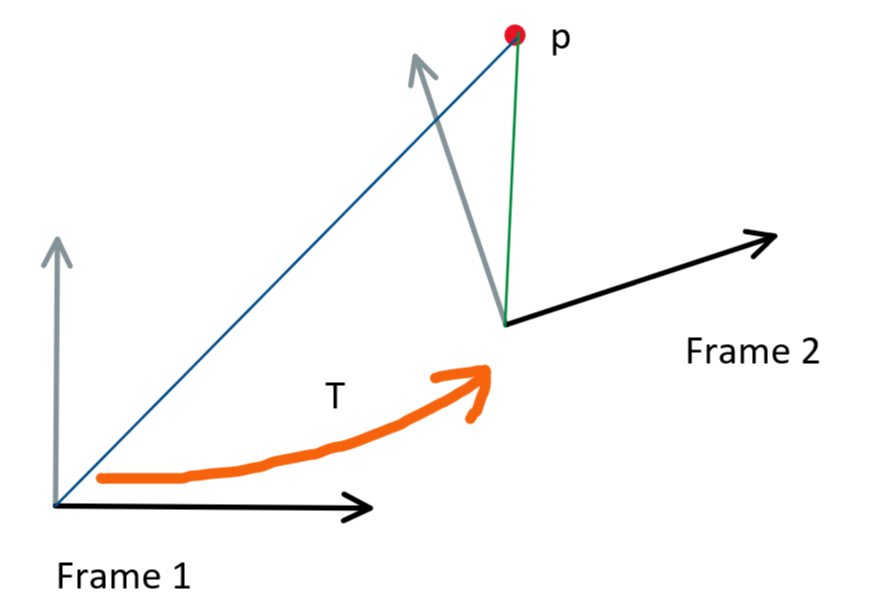
坐标系1经过位姿变换T变换到坐标系2，那么对于两个系中定义的一些点，其坐标变换公式是什么？假设点p在坐标系i下的坐标是 $p_{i}$ ：（为了方便起见，这两个坐标都是齐次坐标） $\begin{aligned} (3) & p_{1} = T p_{2} \\ (4) & p_{2} = T^{- 1} p_{1} \end{aligned}$ 从坐标系1变到坐标系2是变换T，而坐标系1点变换到坐标系2就是 $T^{- 1}$ 。这也可以用左右乘推出的公式来讨论：假设两个坐标系都是相对于一个绝对的坐标系，两个坐标系相对绝对坐标系的变换分别为 $T_{1}, T_{2}$ ，那么对于点p，两个坐标系对应的坐标转换到绝对坐标系下应该是相等的，因为描述的都是绝对坐标系下的点 $p^{*}$ $\begin{matrix} (5) & T_{1} T_{1 - p} p^{*} = T_{2} T_{2 - p} p^{*} \end{matrix}$ 因为 $T_{1 - p} p^{*} = p_{1}$ 且 $T_{2 - p} p^{*} = p_{2}$ ，而上式是由右乘（相对变换）得到的，可以推出公式 $(3)$ ， $(4)$ 来。

2.3 正逆运动学

关于D-H坐标与正逆运动学，这个人的博客讲得很清楚（非常推荐，他的博客写得不错，上一个我觉得写得不错的博客是苏剑林的）：

无处不在的小土

关于正逆运动学的原理以及D-H坐标表示，我就不赘述了，上面链接的博客已经有了。我实现的六轴机器人，正逆运动学的思想是从以上博客以及Wikipedia中学来的，使用的是一个类似PUMA 560的简单带球腕六轴机器人，但是所有的关节中，link twist都与常见模型相反，所以运动学不得不自己推。

在此我只简述一下正逆运动学的思想：

正运动学
逆运动学

实际上就是，给定各个关节的位姿，求解机器人手臂末端的位姿。这是个很容易的任务，就是疯狂地进行位姿变换合成。由于使用D-H坐标描述，使得描述机器人的参数最简，并且也描述了两个关节确定的坐标系之间的相对变换，所以可以轻易地使用位姿变换合成： $\begin{matrix} (6) & T_{6}^{0} = T_{1}^{0} T_{2}^{1} T_{3}^{2} T_{4}^{3} T_{5}^{4} T_{6}^{5} \end{matrix}$ 每个关节相对于下一个关节的位姿变换，在正运动学篇已经进行了详细的讨论，在简单的问题中，也不过就是使用link length, link offset, link twist, link angle计算变换矩阵。

可以把这个问题看作是解方程：已知期望的末端位置，需要求解出每个关节的位姿（比如角度，平移）。复杂问题下，是需要引入优化的方式来求解的（可能没有简单的闭式解），而在一些简单的情形下，可以进行解耦，也就是找到前后不相关联的位姿变换，分解问题为子问题，子问题下就有可能求解出闭式解。带有球腕的问题就是一个典型的简化情形。

我所使用的六轴机器人模型，参数定义如下：

// link offset / link length / link twist / link angle
const std::vector<LinkInfo> init_links = {
    LinkInfo(0.5, 0, M_PI_2,  0.134140), 
    LinkInfo(0.1, 0.8, 0, 0.012189), 
    LinkInfo(0.1, 0, M_PI_2, -0.036790), 
    LinkInfo(0.8, 0, M_PI_2, 1.596749), 
    LinkInfo(0, 0, M_PI_2, -0.222030),
    LinkInfo(0.4, 0, 0, 1.459867)  
};

小土的博客中，使用的是 $- π / 2$ 的link twist，而我这里使用的是 $π / 2$ 。开始我的底部三个关节的求解，完全按照 $- π / 2$ 去推的，这当然会有问题，之后手推了一下 $π / 2$ 的情况。

顶部三个关节如何求解，小土的博客并没有说，但是思想大致还是一样的：将末端点变换到第四个关节对应的坐标系下，使用投影法求解。

2.4 多解问题&可行域

以底部的三个关节以及对应机械臂为例：

Figure 3. 位姿变换示意图

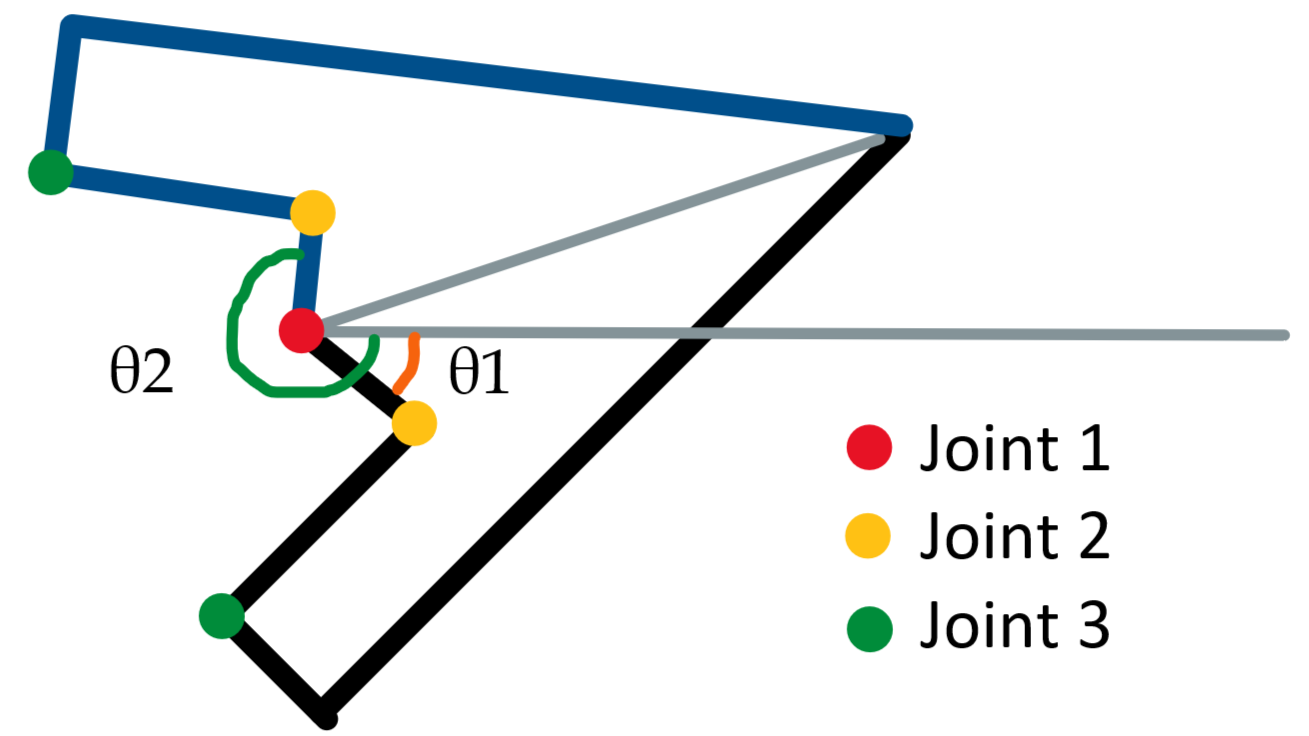
黑色和蓝色分别表示了两种不同解下的机械臂情形。对于同一个球腕位置（也就是右上角的交汇点），可能有两个解，两个解都是需要求出来的，不同的关节会形成解组。比如 $θ_{1}$ 以及 $θ_{2}$ 分别对应joint 2的两个相差 $π$ 的解角度。选取谁？需要根据“能耗最小原则”：哪个解与上一时刻对应的角度最接近，说明运动到对应的状态所需能量损耗最小，机器人应该更倾向于选取这个解。多解问题存在于球腕与底部角度上。

给定末端姿态以及末端的位置，机械臂各个关节也不一定有解，比如：超出长度范围，或是没办法同时满足姿态和位置等等，这些都可能会使得求解结果成NaN，只需要限制在解为NaN时放弃本次控制。

III. Gazebo仿真

我想尝试一下除了rviz之外的可视化方法，rviz版本也已经在Axis6这个库里实现了，这个版本的可视化核心就在tf的使用，也没什么困难的，可视化时碰到的大多数问题实际上都是坐标系或者变换求解错误的问题。除了rviz之外，我能想到也就只有寥寥几个可视化工具：OpenGL以及其封装的Pangolin，Gazebo。由于我从来没有用过Gazebo，故想尝试一下这个新东西。

构建Gazebo机械臂主要有以下三步：

编写urdf（或者xacro）描述机器人，以及相应的gazebo文件（.sdf或者.gazebo以及.world）
构建机器人控制器（transmission），使用gazebo_ros以及gazebo_ros_control进行控制
调参。这一步都能放进来确实是我没想到的。

3.1 描述机器人

ROS wiki上对于描述机器人以及模型的文件是这么说的：

Xacro (XML Macros) Xacro is an XML macro language. With xacro, you can construct shorter and more readable XML files by using macros that expand to larger XML expressions.[1]

Xacro is just a scripting mechanism that allows more modularity and code re-use when defining a URDF model. When using it, what is actually uploaded to the parameter servers (per default as the "robot_description" parameter) actually is a URDF, as that gets generated from the xacro file in the launch file (by expanding the xacro macros used).[2]

这里主要给出四个部分的例子，主要看注释：以下两个部分来自于src/axis6/urdf/axis6.xacro

<!--        此处定义的是机械臂          -->
<link name="world"/>
<!--上面这个link（机械臂）是一个固定的轴，每个urdf都需要带，相当于世界坐标系-->

<!--定义一个机械臂，这里是六轴机器人的底座-->
<link name="base">
<!--collision属性没有写上来，其定义方式与visual类似，定义的是碰撞箱-->
<visual> <!--视觉效果，定义的是我们能观察到的样子-->
  <origin xyz="0 0 0.75" rpy="0 0 0"/> <!--rpy对应轴是xyz-->
  <geometry> <!--定义基础模型：一个长方体，width depth height是xyz-->
      <box size="0.4 0.4 1.5"/>
  </geometry>
  <material name="grey"/> <!--调用material.xacro中定义的颜色-->
</visual>
<inertial>	<!--惯性力学信息-->
  <!--可以认为，此处定义了一个等效几何体，位置与姿态都给出了，并且给了多轴方向上的质量分布-->
  <origin xyz="0 0 0.75" rpy="0 0 0"/>
  <mass value="${mass}"/>
  <!--一种遵循shell类似语法的变量调用-->
  <inertia
      ixx="1.0041666666666669" ixy="0.0" ixz="0.0"
      iyy="1.0041666666666669" iyz="0.0"
      izz="0.13333333333333336"/>
</inertial>
</link>

<!--此处定义的是关节信息，关节是连接机械臂（以及两个不同坐标系）的结构-->
<joint name="joint0" type="continuous">
    <!--joint是机器人机械臂位姿变换的基础，可以认为joint定义的是child link的坐标系-->
	<parent link="world"/>		<!--父系，或者上一个机械臂-->
	<child link="link1"/>		<!--子系，连接的下一个机械臂-->
    <!--关节相对于上一个坐标系，其原点平移偏置以及z轴的相对旋转-->
	<origin xyz="0 0 1.5" rpy="0 0 0"/>  	
    <!--使用child link的哪一个轴或者哪一个方向作为关节转轴-->
	<axis xyz="0 0 1"/>
    <!--电机的力矩以及速度限制（不超过以下两个设置值，这两个参数在【3.3调参】中很重要）-->
	<limit effort="50" velocity="50"/>
</joint>

以下部分来自于src/axis6/urdf/axis6.sdf:

<!-- URDF需要转为gazebo能理解的sdf类型 -->
<gazebo reference="link1">
    <!--设置重力为0，注意此处有Gazebo的bug[3]-->
    <gravity>0</gravity>
    <!--关闭内部碰撞检测，也有bug[3]-->
    <self_collide>0</self_collide>
    <!--两个摩擦系数-->
    <mu1>0.0</mu1>
    <mu2>0.0</mu2>
    <!--还有kp,kd两个参数，用于定义模型的硬度，之前好像是这样的
	假如kp与kd很接近，那么模型会变软，可能陷到地里，kp>>kd时很硬。
	不过我也没有深究过-->
    <material>Gazebo/Black</material> <!--颜色-->
</gazebo>

定义机械臂的重力为0经常出现bug，一会儿说你有 multiple conflicting <gravity> tag 然后给你强制设为<gravity>true</gravity>，又存在这个bug[3]，导致gravity以及self_collide两个标签都不能被正确设置。

以下部分来自于src/axis6/world/axis6.world:

<world name="default">
    <!--引入外部的模型（如果找不到，有些可能会在加载时在网上下载）-->
    <include>
        <uri>model://ground_plane</uri>
    </include>
	<!--...省略部分-->
    <!-- Global light source -->
    <include>
      <uri>model://sun</uri>
    </include>
    <!--最后的我的消重力方式：直接让世界没有重力，嗯，很暴力-->
    <gravity>0 0 0</gravity>
</world>

3.2 传输控制

定义好这些文件后，写一个launch文件，如果编写正确，就能在Gazebo中生成出定义的机器人。但此时机器人是死的，没办法控制。使用gazebo_ros以及相关模块进行控制，这几个包都是需要自己下的，建议直接：

1	sudo apt-get install ros-version-gazebo-ros*

transmission定义的实际上是一个个电机：

<transmission name="tran5">
    <type>transmission_interface/SimpleTransmission</type>
    <!--定义在关节5上的电机-->
    <joint name="joint5">
      <hardwareInterface>hardware_interface/EffortJointInterface
      </hardwareInterface>
    </joint>
    <!--电机-->
    <actuator name="motor5">
      <hardwareInterface>hardware_interface/EffortJointInterface
      </hardwareInterface>
      <mechanicalReduction>1</mechanicalReduction>
    </actuator>
</transmission>

需要配置一个相应的电机config文件(src/axis6/config/axis6_control.yaml)：

axis6:
  # Publish all joint states -----------------------------------
  joint_state_controller:
    type: joint_state_controller/JointStateController
    publish_rate: 50  
  
  # Position Controllers ---------------------------------------
  joint0_position_controller:
    type: effort_controllers/JointPositionController
    joint: joint0
    pid: {p: 15.0, i: 0.001, d: 1.2}
# ...

2-5行是不可少的，此项配置了整个关节状态发布器。剩余的就一个个配置，配置其类型（位置控制电机，速度控制电机）以及pid参数（很难调）。

在加入这些信息之后，再生成Gazebo仿真，使用rostopic list命令可以看到一些新的topic（实际上是gazebo模型subscribe的，但因为没有配置ros端，暂时无publisher），可以直接使用如下命令进行简单测试：

1	rostopic pub <topic_name：比如/axis6/joint1_state_controllers/command> <topic_type:一般是std_msgs::Float64> "data: <控制量，比如:1.0>"

剩下的事情就是写一个控制节点，发布对应消息就能进行控制了，这里就不赘述了。

3.3 调参

仿真，顾名思义，一定要真。即使我把摩擦关了，碰撞检测关了，重力关了，控制也并没有想象的那么简单。问题主要是：

机械臂的质量以及质量分布设计得不合理（比如末端很重）
PID参数 + 电机limit（见xacro文件按）设置的不合理。

导致以下三个问题（折磨了我一下午）：

电机驱动力不够 + pid参数过小时，又慢又超调
电机驱动力充足 + pid参数较大时，机械臂抖动严重（末端尤为严重）
电机驱动力充足 + pid参数过大时，可能会炸开。。。机械臂直接飞了，这也太真实了

解决方案当然就是一个个电机调：

joint0_position_controller:
	pid: {p: 15.0, i: 0.001, d: 1.2}

joint1_position_controller:
	pid: {p: 10.0, i: 0.001, d: 0.8}

joint2_position_controller:
	pid: {p: 5.0, i: 0.001, d: 0.1}

joint3_position_controller:
	pid: {p: 1.5, i: 0.001, d: 0.04}

joint4_position_controller:
	pid: {p: 1.1, i: 0.001, d: 0.08}

joint5_position_controller:
	pid: {p: 0.25, i: 0.0001, d: 0.0002}

从最底部的关节开始（它应有的驱动能力最大，因为负载最大），关节号越高，其后的机械臂越少（载荷越小），那么显然，limit中的effort以及velocity应该越小，PID参数越小，机械臂也尽可能在末端变轻。

IV. 效果展示

最后的效果也就是：末端可以三轴方向平移，以及绕某一轴旋转。我复用了之前写的键盘控制函数（在LiDARSim2D库内）（多按键触发），故运动是可以合成的：

rviz：使用tf以及visualization_msg::Marker进行可视化：

Video 1. rviz仿真结果

Gazebo：花了好几个穿模的长方体（随便画的，没必要搞机械设计了）:

Video 2. Gazebo仿真结果

Reference

[1] ROS wiki: xacro

[2] URDF or Xacro?

[3] Incorrect URDF to SDF conversion of gravity and self_collide tags #71