A Duality Problem of Representations
Duality
I. Introduction
In a slide talking about 3D geometry and deep learning, I found something interesting: one question, of which I can not get rid. This is a duality question about representations:
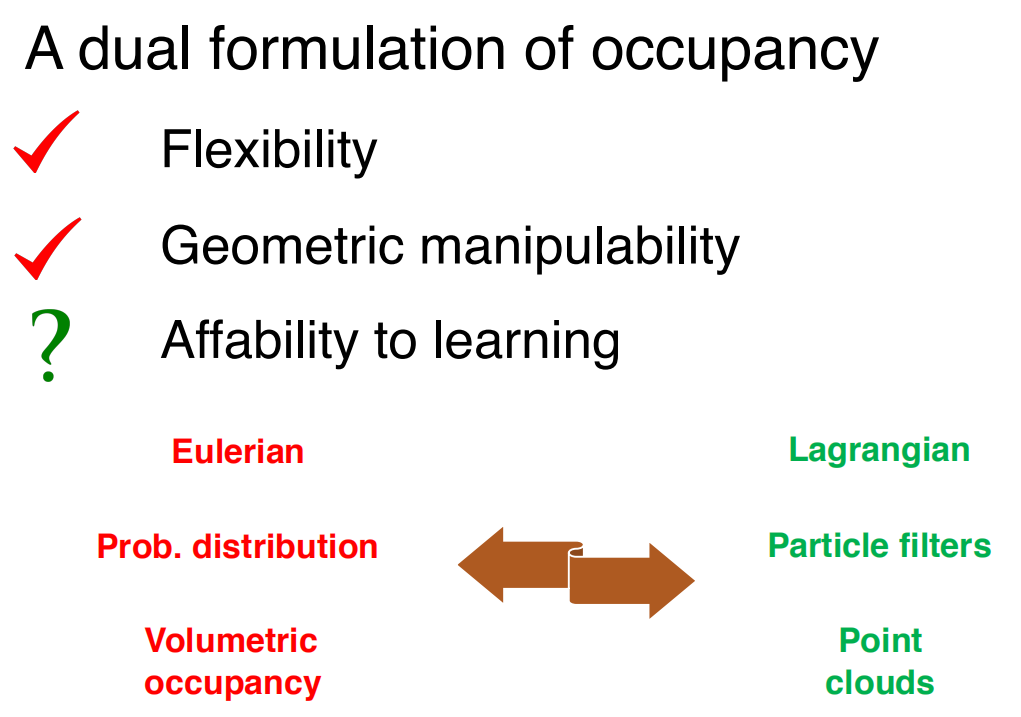
These problems lingered in my head:
- Why and how we can regard probability distribution and particle filters as dual counterparts to each other?
- Same question for occupancy map and point clouds, as they seem to be, according to the figure above, the representations under different specifications?
So I took some time to sink in this problem. This post is therefore the summarization of my thoughts.
II. About two specifications
Eulerian and Lagrangian specifications are just two perspective of perceiving the world. Wikipedia illustrate these two specs with a good example (though it is talking about flow field):
The Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the pathline of the parcel. This can be visualized as sitting in a boat and drifting down a river.
The Eulerian specification of the flow field is a way of looking at fluid motion that focuses on specific locations in the space through which the fluid flows as time passes. This can be visualized by sitting on the bank of a river and watching the water pass the fixed location.
III. Thoughts
You will find that this description is kind of similar to the famous "Wave–particle duality" . Somehow, the brilliant physicians device the idea of probability and "uncertainty", representing any given location of the physical world with the probabilities of different kinds of particles being present (since we know that in physics, electrons are actually a "probability cloud" around the nucleus), which resembles to occupancy grid representation. However, another intuitive representation of the world is that: The world composes of myriads of small individual particles. Now this is kind of like the point clouds, yet in the real world, the "point clouds" are much denser and complex.
This would mean that, (by my understanding):
- Eulerian specification tends to directly model the space (no matter what space this is), for each location within the interested space, we model the attributes (e.g. temporal or probabilistic) of it.
- Lagrangian specification uses individual attention, or to say, the nonparametric, sampling-like approach to represent the interested space.
Therefore, the duality between probability distribution and particle filters are quite straight forward:
Probability distribution comes in many forms. There are basically two types: parametric and nonparametric. By "probability distribution" mentioned above, I mean the parametric approach.
The salient feature of parameterized approaches is: They are commonly defined on a fixed space, in this "fixed space", we can calculate the pdf of this distribution. However, nonparametric approaches are "sample-based", for example: KDE (kernel density estimation) and particle filters. For the former one, given location and parameters, the probabilistic attributes are fixed, yet for the latter one, the given location might just be "void" in terms of samples, therefore the information of the given location is subject to all the particles and every individual matters! The focus is different, one is on the fixed location in the space, and the other is on each individual. This is just the characteristic of parameterized distribution and particle filter method.
Say, if we have all the correct poses and transformations between the frames (point clouds), we now have two choices of map representation: Grid map (or voxel map) vs. point-clouds (and its variants like the representation I've been working on). For each grid (voxel) in the map, the focus given is "Eulerian", since we focus on the specific location. As for point clouds, it (yes I am not going to use plural) can be seen as the "particle filters" of walls and obstacles, which is sample-based and "Lagrangian".
IV. Can we dig deeper?
Now we know that, point cloud (and its variants) representations are the dual counterpart of occupancy map, yes but... what is the point? How this is going to help us? Let's talk about the merge of observations!
Formulation: the example of merge is that, if we observe a wall in one frame and in the successive frames we observed the same wall. Since we have the correct transformation, how we going to use the multi-view observation to get a more accurate wall?
For Eulerian method like occupancy grid, merge process is naturally incremental! Because Eulerian methods explicitly models each location, given the correct point cloud registration result, the update of occupancy grid is easy (using LiDAR model and the idea of "beam hitting the obstacles").
Unfortunately, merge for Lagrangian approaches is difficult to tackle with. The main goal is to build a incremental merge algorithm. Intuitively, merge for nonparametric approaches usually requires "total rebuild". For instance, consider every observed wall a particle filter. Every new observation might add new information to each particle filter, therefore for the final state a particle filter represents, we might need to calculate the updated stated from the scratch with no previous computation reuse (that what I currently believe). To my current belief, the incremental merge can only be implemented at a coarse-grained level.
Reference
[1] Hao Su (Stanford University): 3D Deep Learning on Geometric Forms, pdf
[2] Wikipedia: Lagrangian and Eulerian specification of the flow field