Distance Metrics on Point Clouds

Posted on Edited on In Views: Symbols count in article: 4.8k Reading time ≈ 4 mins.

Distance Metrics

I. Introduction

​ 近期的研究有探究一个好的尺度的需求：判断配准是否完成。针对这个问题，我脑子里想的第一件事就是：判定两个点云在某个尺度上是否相近。带着这个目的，我结合之前看过的文献，在解决这个问题的方案中补充了一些新的内容。本文主要包括一下几个内容：

低维的最邻近点并不意味着结果能很好地适用于任务，高维的最邻近才是最终的追求。就像你和你异地的（男）女朋友，你们地理上不是最邻近，但是在某个高维空间中，确实是最邻近的，这就是为什么我们需要变换尺度与维度看问题。--- 哲♂学家 千越 · 让 · 德 · 叠buff · 何

II. 点云距离尺度

2.1 引

​ 在某些任务中，我们希望得到两个点云之间的一种接近程度的描述。比如在配准任务中，两个点云中相似的点或特征越接近，那么意味着配准结果越好。但由于点云表征不同于Grid、体素或者深度图等表征方式，点云是无结构，无顺序的。一些简单的比较方式不再适用，比如说：我有两个体素化的点云，这两个点云的接近我可以使用两个体素相减（体素内部含有占用概率），最后对这个结果张量求范数即可。这就是论文中说的：

They are not a function on a grid, point clouds cannot be compared using a common metric (such as Euclidean metric)

​ 一般来说点云的距离尺度有三个非常著名的距离：Hausdorff距离，Chamfer距离，Earth Mover's距离（EMD，或者叫Wasserstein距离，又或者叫Kantorovich-Rubinstein距离）。
Hausdorff Chamfer Earth Mover's
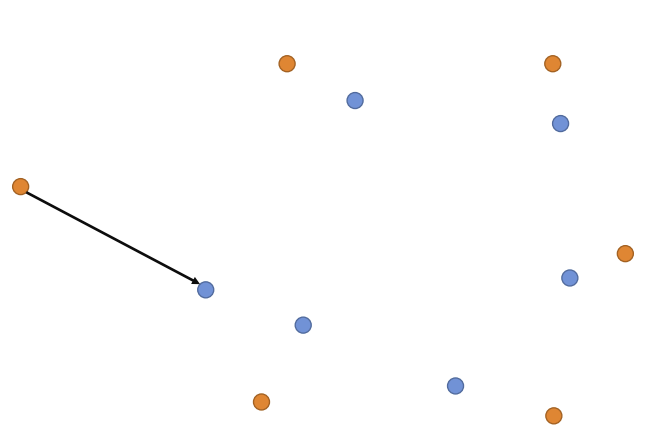
Figure 1. 三种常用的Distance metrics图示[1]

2.2 Hausdorff

​ Hausdorff距离是一种：worst-case的距离描述，它描述了两个点云之间的一个距离上界。通俗地说，Hausdorff距离（单边）是这样定义的，假设我们有两个点集A，B：

  • A中任意一个点p，都能在B中找到其最邻近点q。那么A中每个点有一个最小距离：\(d_i=\mathop{\min}_{q_j}\Vert p_i-q_j\Vert\)
  • 取A中每个点最小距离的最大值（也就是最邻近距离的最大值）

​ 完整的Hausdorff应该是：

  • 最后反过来，B中也有同样的一个最邻近距离的最大值。求A->B,B->A这两个距离中的大者。正式定义应该是：

\[ \begin{equation}\label{haus} d_{haus}=\max \left\{ D(A,B),D(B,A)\right\},\text{ where }D(X,Y)=\mathop{\max}_{p_i} \mathop{\min}_{q_j}\Vert p_i - q_j\Vert,p_i\in X,q_j\in Y \end{equation} \]

​ 这个公式的问题还是很大的，此距离很容易受到外点（outliers）的影响。在文献中已经提到了此距离的修改版，简单来说就是截断Hausdorff距离，超过一定阈值的\(\mathop{\min}_{q_j}\Vert p_i - q_j\Vert\)不会被记录。但不管怎么样，这个距离都是一个最坏距离的衡量。

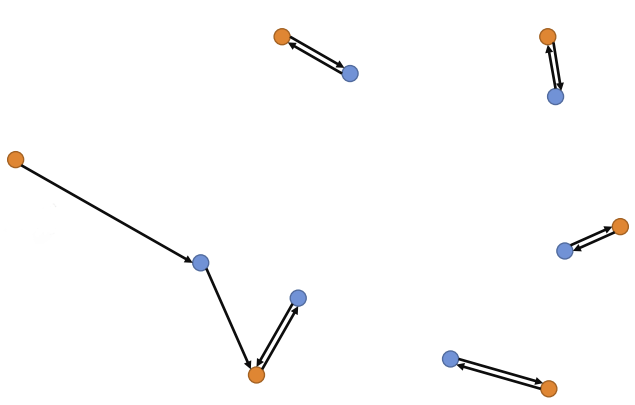
2.3 Chamfer

​ Chamfer距离是一种平均意义上的距离，其意义很好理解：平均的最近点距离，定义如下： \[ \begin{equation}\label{chamfer} d_{chamfer}=\text{normalize}(\sum_{q_j\in B}\mathop{\min}_{p_i}\Vert p_i-q_j\Vert + \sum_{p_i\in A}\mathop{\min}_{q_j}\Vert p_i-q_j\Vert) \end{equation} \] ​ 这个距离倒是没什么好说的，它是一个平均意义上的距离，实现起来比较方便，但是对基于特征的方法并不友好（高维最邻近点计算很恶心）。很常用，因为Chamfer distance相对于EMD存在一个优点：它并不要求建立双射，也就不要求两个点集的大小一致，可以有一对多联系。在骷髅融合者这篇博客中，我分析了一下作者提出的Composite Chamfer Loss，作者通过修改反向距离，建立了一个非对称的，针对不同稠密程度点云的Chamfer loss。

2.4 Earth Movers'

​ 这是最理想的距离尺度，其基本定义为： \[ \begin{equation}\label{emd} d_{EMD}(A, B)=\mathop{\min}_{\phi: A\rightarrow B}\sum_{p_i\in A}\Vert p_i - \phi(p_i)\Vert \end{equation} \] ​ 其中\(\phi\)是点集A到B的一个双射。由于是双射，上式是一个双向对称的距离。在2.3中已经说了，双射就要求集合大小一致，通常情况下，这并不容易满足，特别是在SLAM背景下，部分观测（见3.3）导致一般用不了这个距离。但在一般意义下，这个距离是最优的：

Figure 2. EMD与CD的比较，这张图的结果是很显然的[1]

​ 接下来到了科普思考时间。为什么这个距离叫做Earth Mover's（我称之为，搬砖者距离）？ 维基百科上这么说

In statistics, the earth mover's distance (EMD) is a measure of the distance between two probability distributions over a region D. Informally, if the distributions are interpreted as two different ways of piling up a certain amount of earth (dirt) over the region D, the EMD is the minimum cost of turning one pile into the other; where the cost is assumed to be the amount of dirt moved times the distance by which it is moved.[2]

​ 嗯，intuitively，确实是这样的。所以称这个距离为搬砖者距离也没有问题。

III. DPDist

3.1 基本思想

​ Deep Point Cloud Distance，则是一种新的距离尺度，相当于是一种基于深度学习输出的误差函数定义（本身DPDist也就可以当做误差函数）。其最主要的思想就是：

我们不应该直接去比较两个点云，这是非常不优雅的。点云的比较，点云之间的距离，说白了应当是：其中一个点云的每一个点，到另一个生成点云原本的真实世界障碍物表面的距离。不应当是直接的：点-点距离，应当是：点-面距离。

​ 这个想法确实是自然的，点云表征具有稀疏性，除非两个点云在物理世界的采样点完全一致，否则点-点距离再如何好都只是一个近似罢了。

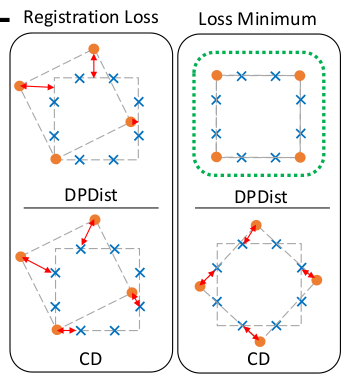
Figure 3. 论文中有关DPDist与CD（Chamfer distance）的比较

​ 但新的问题同时会出现：真实世界的表面，我们是无法获得的，只能从点云中估计出来。表面估计可以是全局的，也可以是局部的。但一般来说，全局的非常难做：我们要从一个2D点云中，估计一整个连续函数用来表征点云的采样表面，这可能还稍微容易一些，但是3D，emmm，文中说某个网络想做这个事，用了亿点点参数，也没做好。

​ 局部表面估计首先简单，参数量可以小，并且，局部近似度能更高（就比如，局部线性化，局部范围越小，近似度可以越高）。那这就产生了两个问题：

  • 我怎么能确定，点云A上的给定点p，应该使用点云B的哪一块计算局部表面来估计距离？
  • 局部表面如何估计，计算如何进行？

3.2 作者的魔法解决之路

​ 首先，我们需要点云的全局特征。说是全局，不如说是很多局部特征的组合，分块儿的局部特征，合成一个全局特征。作者使用3DmFV（没细看过这篇论文），大概思路就是：

​ 首先将空间划分为一个个的Grid（可以是一个粗粒度的划分），假设空间中存在\(K\times K\times K\)个grid。由于原点云已经生成了一个N成分的混合高斯模型（GMM）（也就是一个多高斯分布加权的分布）， 在不同的Grid中，都可以求到一个Fisher Vector（也就是综合了Grid局部信息的一个GMM梯度）。由于Grid划分是固定的，固定就意味着训练方便。

\(K\times K\times K\)每个格提取GMM的特征，得到一个四维张量：\(K\times K\times K\times F\)。这是整个点云的全局特征，它是一种固定的，有结构的特征。假设这个特征是点云A的，我们将之记为：\(L^{S_A}\)

对于每个点云B中的query点（要求点-面距离的点），总是在A中寻找里query点(\(b_i\))最近的grid，在最近Grid周围扩散n步，形成一个\(k\times k \times k\)大小的子grid，k当然是奇数，因为最近点是中心，向外扩散n步则\(k=2n+1\)。

这\(k\times k \times k\times F\)大小的张量（subgrid的特征）将被concat到\(b_i\)的点云坐标上（好魔法啊，又开始concat了）。最后过一个三层全连接层，得到距离。

由于存在对称性，A->B以及B->A的DPDist都需要计算，最后按照点数平均，得到最终的距离。

Figure 4. DPDist的网络结构

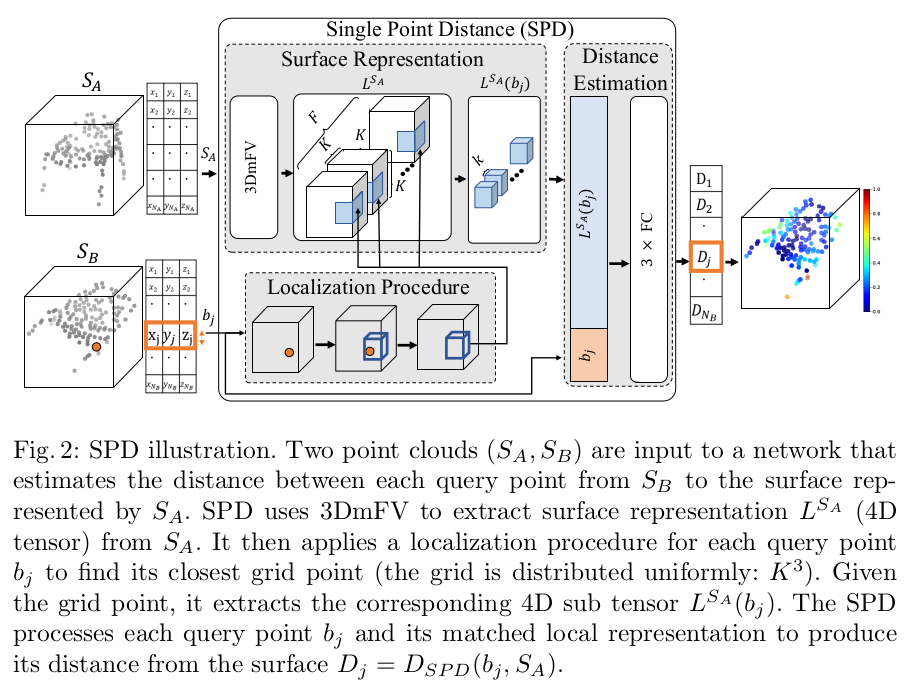
3.3 个人觉得存在的问题

（1）部分观测。整个网络还是限定了：每个点都能有个属于自己的表面。这在一些object点云数据集上是成立的，但是在SLAM系统中很难成立。由于使用最近grid，那些两个观测点观测的对称差集中的点，会被错误地assign到一个不属于自己的表面上，这在计算中会导致问题（不准）。所以让我感到迷惑的是，作者将DPDist用在了PCRNet中（PCRNet是一个。。。emmm很魔法的网络），作为点云配准的距离尺度，替换了原来的EMD。看了它的实验就知道：人家搁这搞一张椅子的配准：

Using the ”Chair” category and following [20], we randomly generate 5070 different transformations for training and other 5070 transformations for testing.

​ 这种物体级数据集当然不会遇到部分观测问题。事实上，部分观测问题也限制了EMD（毕竟EMD希望能建立一个点集之间的双射），部分观测导致双射无法建立。并且在SLAM问题下，对同一个物体进行不同分辨率下的观测，也直接限制了EMD的使用。

（2）3DmFV？虽然，论文中说3DmFV特征描述比PointNet描述更好，但是3DmFV却引入了“体素化”这种东西（虽然可以是一个很粗粒度的）。但这是否会带来accuracy-memory tradeoff？高斯表征与混合高斯模型的描述能力以及是否有正确的物理含义也是没有说清楚的。

Reference

[1] Hao Su (Stanford University): 3D Deep Learning on Geometric Forms, pdf

[2] Wikipedia: Earth Mover's Distance