Swin Transformer 复现

Swin Transformer

---

I. Intros

​ Swin Transformer获ICCV best paper之后，就总有很多人提起它。个人在前段时间复现了一个与ViT相关的工作（Compact Convolution Transformer），感觉实现太简单（训练难），遂想尝试一些更加复杂的工作。同时我当然也想看看best paper到底是什么水平。此论文写得很清晰，实验做得非常漂亮，思想也很有趣，不过可以说是一篇typical神经网络文章：一个公式都没有（attention公式以及复杂度计算公式不算）。个人虽然惊叹于其SOTA表现，但由于存在不可解释的魔法，也始终觉得很膈应。本文是我在复现过程中的整理的一些思路和我觉得本论文中疑难之处及其理解。复现见：Github/Maevit(这实际是ViT的复现repo)

​ 论文原文：Liu, Ze, et al. "Swin transformer: Hierarchical vision transformer using shifted windows." arXiv preprint arXiv:2103.14030 (2021).

Figure 1. 艺术之国：还有一个XJTU的（MSRA nb）[1]

II. Some Points

2.1 复杂度

​ 复杂度计算（二次部分）：图像大小为\(h\times w\)，那么由分块大小为M，可以得到\(h\times w/M^2\)个patch，每个pacth的大小是\(M^2\)。而对于一个patch，相当于是用一个小ViT，对\(M^2\) patch token进行 “global” attention，复杂度\(O({(M^2)}^2)=O(M^4)\)故总复杂度：\(O(M^2hw)\)，对于通道数为2C的embedding而言，就如论文所说的：\(O(2M^2hwC)\)

​ 这么说Set transformer中的induced point 机制，可能也可以应用到这里来？

2.2 Masked Attention

​ Masking 很好理解，由于原图是物理上连续的，经过了一次循环移动操作之后，循环移动的分界面是物理上不连续的区域，故在进行注意力机制处理时不能包括分界面两边的区域。比如：

Figure 2. 循环移动示意图

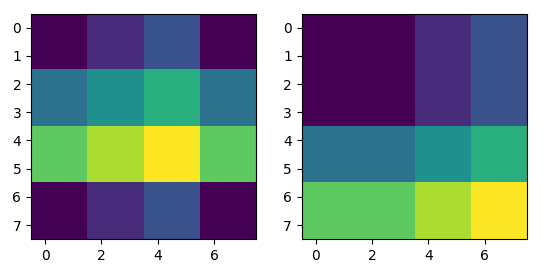
​ 右边是循环移动前的图，左边是循环移动后的图。我们希望，能够分块进行attention。个人的理解大概是这样的，其实这个很简单：我使用官方实现做了一个小实验之后，大概明白了其包含的思想（但是这个矩阵操作我可能做不来，有点妙，我顶多自己在这循环）：

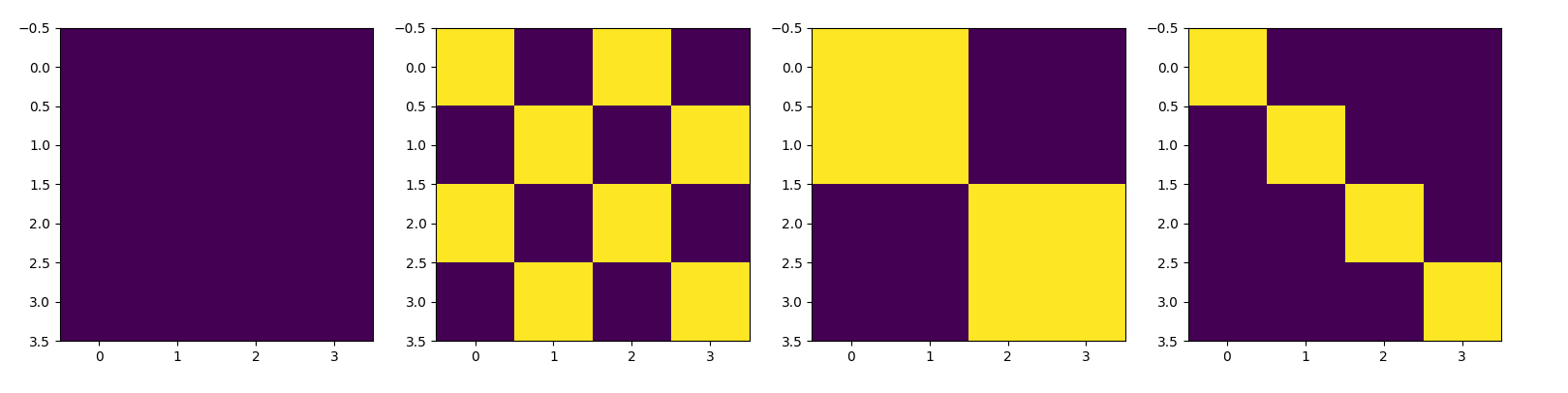
​ 这个小实验的设置大概是这样的：图像大小为 4 * 4，window大小为 2 * 2，偏移为1 * 1，得到的四个mask长这样(其中，黄色为0，紫色为-100）：

Figure 3. attention mask

​ なんで？可以看下面这个可视化：我们将16个块编号，并进行循环移动，循环移动后的图和原图：

Figure 4. 循环移动illustration

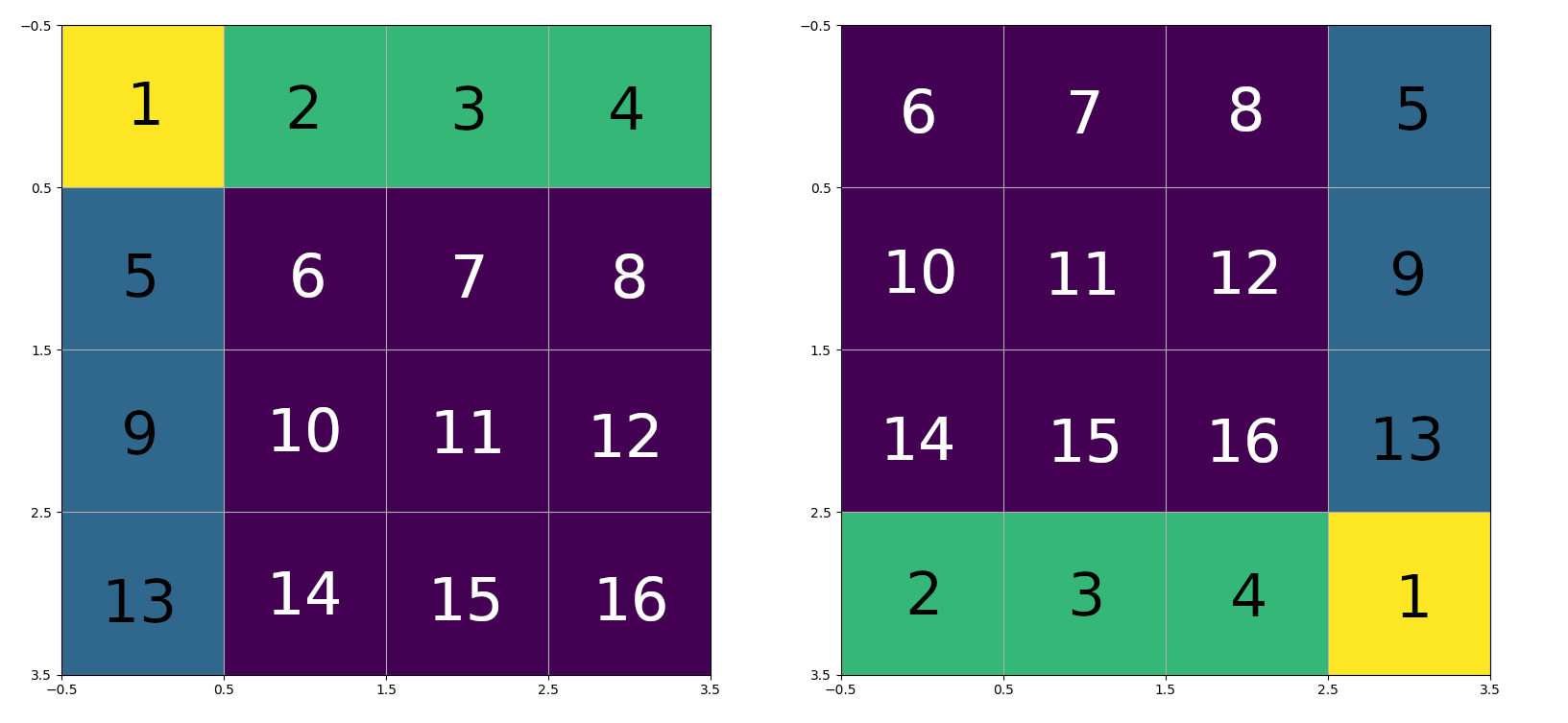
​ 注意力操作将把一个window内的元素flatten，比如第一个window内的 ((6, 7), (10, 11)) -> (6, 7, 10, 11)。flatten操作是行优先的。故对于第一个window而言，由于内部的所有元素都是原图中的元素，可以直接进行attention操作，故attention mask值全为0。

• 第二个window：((8, 5), (12, 9)) -> (8, 5, 12, 9)。由于(8, 5) 以及 (12, 9)两两不能做attention操作，故mask应该就是figure 2中的第二个图。比如图中4 * 4矩阵的(0, 1)位置是-100，代表了块8与块5之间的attention logit值应该加一个很大的负偏置，也就是消去了两个块之间的关联。
• 此后的两个window都能很快以这个思想推出。

​ 代码中则是这么实现的：

H, W = input_resolution
img_mask = torch.zeros((1, H, W, 1))  # 1 H W 1
h_slices = (slice(0, -self.window_size),
            slice(-self.window_size, -self.shift_size),
            slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
            slice(-self.window_size, -self.shift_size),
            slice(-self.shift_size, None))
cnt = 0
# 分块赋值操作 经过分块赋值之后，一个window内可以进行attention操作的块为同一个id
for h in h_slices:			
    # 比如cnt = 0，根据h_slices与w_slices的第一个元素，赋值给[0:-win_size, 0:-win_size] 这样是没有问题的
    for w in w_slices:							 
        img_mask[:, h, w, :] = cnt
        cnt += 1
mask_windows = window_partition(img_mask, self.window_size)  # nW, window_size, window_size, 1 --> 分window操作
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)	# flatten操作：（所有batch的所有window，window内所有块）
# 此处魔法：unsqueeze(1) 导致 mw 为 (B, 1, N), unsqueeze(2) 导致 mw 为 (B, N, 1)
# 相当于计算时，一个按行repeat（前者） 一个按列repeat（后者），相当于自己减自己的转置 就可以得到：相同id的位置是0，不同的是一个非0值
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)		   
# 所有非零值变为-100
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))

III. Relative Position Bias

3.1 Positional Embeddings

​ 实际上，我对position embeddings（特别是non-learnable PE）到底是如何工作的还并不是特别清楚。position embeddings 如何表示位置 是否有直观的理解？

Moreover, positional embeddings are trainable as opposed to encodings that are fixed.

​ 意思大概是这样的，一个简单的positional embeddings（只在初始时加入的那种）可以被如下公式表示： \[ \begin{equation}\label{pos} \epsilon_{ij}=\frac{\text{lin}_q(x_i)(\text{lin}_k(x_j))^T+\text{lin}_q(x_i)(\text{lin}_k(p_{j}))^T}{\sqrt d_k} \end{equation} \] ​ 个人认为更加合理的表示应该是（如果对于初始就加到embedding上的position embeddings来说）： \[ \begin{equation} \epsilon_{ij}=\frac{\text{lin}_q(x_i + p_i)(\text{lin}_k(x_j + p_j))^T}{\sqrt d_k} \end{equation} \] ​ 在某篇博客中的表述是这样的：对于公式\(\eqref{pos}\)中的\(\text{lin}_k(p_{j})\) 我们将其改为\(p_{ij}\)，此处\(p_{ij}\)是整个positional embeddings的(i, j)元素，表示了处于位置i的query相对于处于j位置的key的位置关系，可以理解成是与位置有关系的相关性。比如，在CV应用中，常见的inductive bias就是：临近关联性，即使经过分块，相邻的块与块（或者位置相近的）之间也是有关联性的。一般的positional embeddings，临近的两个位置，positional embeddings的某个metrics（比如差值、点乘）可能比较小（大）。

​ 本节的重点是讨论相对位置嵌入，因为绝对位置嵌入之前已经实现过了（就很简单），特别是learnable positional embeddings，就没有什么好讨论的。我们已经说了，相对位置嵌入是为了解决绝对位置嵌入无法编码任意多的位置的缺点。这里我讨论一下music transformer中的relative positional embeddings（计算比较简单）： \[ \begin{equation} \text{Attn}_{rel}=\text{softmax}(\frac{QK^T+S_{rel}}{\sqrt{d_k}})V,\text{ where }S_{rel}=QR^T \end{equation} \] ​ 我感觉上面的公式怪怪的，因为：

• \(Q\)（query）不仅与映射\(W_q\)有关，与数据本身也是有关系的，不同的图像\(Q\)差别很大，那么一个\(R\)怎么能很好捕获到不同query向量之间的关联性？举一个具体的例子：

\[ \begin{equation} A=\begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \\ \end{pmatrix}\xrightarrow{\text{flatten}}(1,...,16) \end{equation} \]

​ 上例子中（CV二维），元素1在位置上应与（2，5）有着最紧密的关系，那么应该\(QR^T\)计算的结果在(0,1)(1,0)位置都较大（softmax之后也会较大），但是\(QR^T\)的计算中，对任何\(Q\)而言\(R\)是相同的，不同的矩阵\(A\)，元素1与元素2、5均应该有此关系，那么在\(Q\)改变的情况下，什么机制保证了\(QR^T\)的稳定性呢？这已经是人类难以理解的魔法了，例如：相邻两patch，由于位置临近可能确实存在一定关系，对于不同的数据都有这样的共性，\(R\)也只能去学可以泛化的共性了。

3.2 RPE的实现

3.2.1 Music Transformer

​ 不同的relative positional embeddings实现有一些差别。最早期的relative positional embeddings 有这样的问题：空间复杂度是\(O(L^2D)\)。因为：

​ 求解relative positional embeddings带来的距离logit，需要得到query与PE之间的点乘。考虑一个head的情况，Q的形状应该是：\((L,D_h)\)，其中L是序列长度，\(D_h\)是对应head的embedding dimension。我们希望知道，query的每个向量（embedding）与不同距离位置的相关程度，比如，\(Q\)的第i行（序列中第i个token的embedding），需要计算其与各个位置的分数，那么就需要： \[ \begin{equation} \text{logit}(q_i)=q_iE_r^T,\text{ where }E_r=(\text{PE}_0,...,\text{PE}_{L-1}) ,\text{PE.shape}=(1,D_h) \end{equation} \] ​

​ 而直接计算\(QE_r^T\)的结果并不是我们想要的：它算出来的矩阵和我们需要的矩阵分别是这样的,其中\(v_{i,j}\)表示的是第 i 个query向量和 与其距离为j的位置的logit bias。 \[ \begin{equation} A=\begin{pmatrix} v_{0,0} & v_{0,1} & ... & v_{0, L-1}\\ v_{1,0} & v_{1,1} & ... & v_{1, L-1}\\ \vdots & \vdots & \ddots & \vdots \\ v_{L-1,0} & v_{L-1,1} & ... & v_{L-1, L-1}\\ \end{pmatrix},B=\begin{pmatrix} v_{0,0} & v_{0,1} & ... & v_{0, L-1}\\ v_{1,1} & v_{1,0} & ... & v_{1, L-2}\\ \vdots & \vdots & \ddots & \vdots \\ v_{L-1,L-1} & v_{L-1,L-2} & ... & v_{L-1, 0}\\ \end{pmatrix} \end{equation} \] ​ 以A的最后一个行的首尾两个元素为例。\(v_{L-1,0}\)表示的是最后一个embedding与自身的位置偏移logit偏置，而最后一个元素\(v_{L-1,L-1}\)表示的则是：最后一个embedding与相距L-1距离位置的logit偏置。而我们反过来看最后一行的self attention，最后一行的self attention的结果logit中，最后一个元素表示的才是自己与自身的attention值。

​ 也就是说，直接计算\(QE_r^T\)是不行的，这样计算会导致self attention 与 positional attention求出的logit在逻辑意义上的错位。B才是我们需要的：从对角线元素的下标就能看出。

​ 那么如果要进行直接的矩阵运算，一个简单的想法就是：我可以直接计算一个中间矩阵R，R包含了（旋转过的）\(E_r\)，这样，对于每一个query向量，其计算都应该是正确的，再直接矩阵相乘（毕竟能直接矩阵运算的，CPU上可以SIMD，GPU上并行度好）。那么可以将\(Q\)与\(E_r\)处理成这样： \[ \begin{equation} Q.\text{shape}=(L,1,D_h),R.\text{shape}=(L,L,D_h),S_{rel}=QR^T \end{equation} \] ​ 其中，R第一维度下每一个元素都是一个\(E_r\)。这种实现简单直观，但是，内存开销很大，长序列不友好。既然相对位置嵌入是为了解决长序列建模问题，那么自然其时间复杂度以及空间复杂度不能因为序列长度增长而变得难以接受。于是，music transformer的作者提出了一种空间复杂度为\(O(LD)\)的方法。

​ 很显然，直接计算\(QE_r^T\)已经包含了所有需要\(S_{rel}\)的信息，只不过对应关系错了（位置有误）。如何通过\(QE_r^T\)的结果计算\(S_{rel}\)？

​ 作者用了一个巧妙的矩阵操作：pad + reshape：图示一下：

Figure 5. skewing操作图示

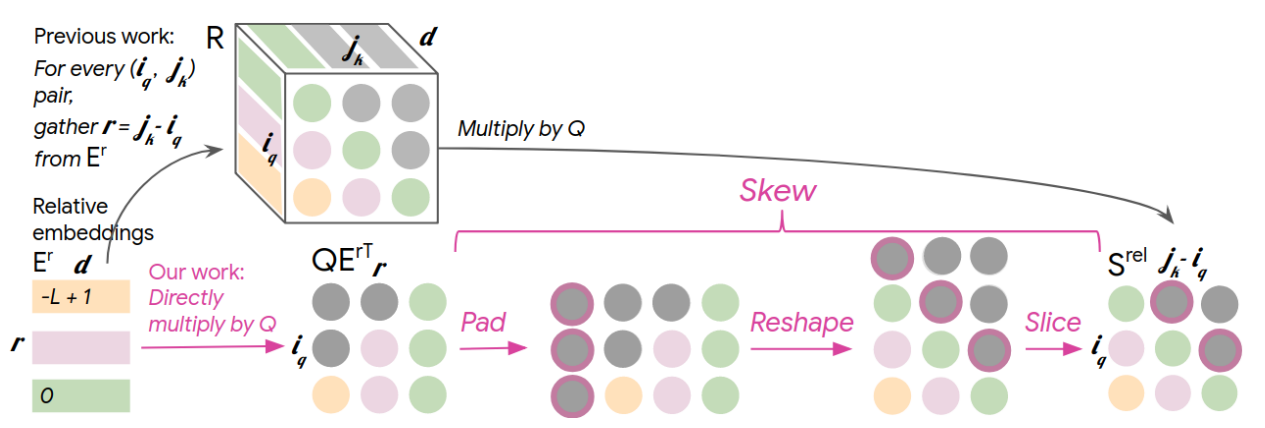
​ 作者在文章中说到：

Pad a dummy column vector of length L before the leftmost column.

​ 这样再reshape之后，导致了一个问题，原有的有效元素丢失，引入的矩阵中出现了一些dummy elements。并且感觉出现了：第i行元素被挤到第j行的情况。举个例子，正常情况下，一个长度为5的序列，\(S_{rel}\)的index 2行应该是（循环右移2）： \[ \begin{equation} (1,2,3,4,5)\rightarrow(4,5,1,2,3) \end{equation} \] ​ 所以个人感觉padding是有点问题的，应该直接进行一些变换：线性变换是不可能的（不存在一个矩阵R，可以将第一行旋转0，第二行旋转1，第三行旋转2,...，因为如果存在这样的矩阵，则对于矩阵A，A只有第一列全是1，其他全是0，这样显然没有逆的矩阵，R成了它的逆）。个人觉得，一个简单的实现应该是：计算一个循环移动过的索引矩阵，比如我知道本次需要计算的seq length为N，那么我首先计算一个大小为\(N * N\)的索引矩阵，根据此索引矩阵取\(QE_r^T\)元素，但这样又引入了一个\(O(N^2)\)复杂度的存储开销（比\(O(N^2D)\)小了很多，16位一般就够用，相当于几张大型双通道图像）。

可能这是优雅的实现，毕竟我发现swin也是这么求的。music transformer在干啥？是我没看懂还是本身就是错的？不应该错了啊。

3.2.2 感觉正确的实现

​ 所以，我带着怀疑态度看了一下music transformer以及swin transformer的实现。music transformer还真是这样写的：

if self.relative_pos:
    #apply same position embeddings across the batch
    #Is it possible to apply positional self-attention over
    #only half of all relative distances?
    Er  = self.Er[:, embedding_start:, :].unsqueeze(0)
    QEr = torch.matmul(queries, Er.transpose(-1,-2))
    QEr = self._mask_positions(QEr)
    #Get relative position attention scores
    #combine batch with head dimension
    SRel = self._skew(QEr).contiguous().view(b*h, t, t)

​ 其中的skew毫无保留地实现了论文的思想，个人感觉非常诡异。个人觉得原因可能是：它是music transformer，只保留一个方向的attention，故可能有所不同？

​ 个人思考后出来的实现与这篇博客：AI Summer:How Positional Embeddings work in Self-Attention (code in Pytorch)给出的实现方法很相似。但在swin transformer中，我还是忽略了一个很重要的问题：普通的序列一般是一维的，所以展开之后的相对距离实际上是一维度量： \[ \begin{equation}\label{rm} \begin{pmatrix} 0 & 1 & 2 & ... & L-1\\ -1 & 0 & 1 & ... & L-2\\ -2 & -1 & 0 & ... & L-3\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -L+1 & -L+2 & -L+3 & ... & 0\\ \end{pmatrix} \end{equation} \] ​ 而对于二维图像中的embeddings，注意两点：

• 相对位置编码以及绝对位置编码解决的是同一个问题，所以实际上是可以相互转化的
• 正负方向有别，x+1以及x-1是不一样的，但是x，y方向也是不一样的

​ 我们以 window size = 2 的情况来说明swin transformer中的“相对位置 bias（至于为什么要 加粗以及“双引号”，之后会说到）”的实现：对于以下A，B，C，D四个位置的像素每个位置相对于其他不同位置像素的二维距离分别是（注意有方向） \[ \begin{align} &\text{image}=\begin{pmatrix} A & B\\ C & D \end{pmatrix}\\ &A:\begin{pmatrix} (0,0) & (0,1)\\ (1,0) & (1, 1) \end{pmatrix}\\ &B:\begin{pmatrix} (0,-1) & (0,0)\\ (1,-1) & (1, 0) \end{pmatrix}\\ &C:\begin{pmatrix} (-1,0) & (-1,1)\\ (0,0) & (0, 1) \end{pmatrix}\\ &D:\begin{pmatrix} (-1,-1) & (-1,0)\\ (0,-1) & (0, 0) \end{pmatrix}\\ \end{align} \] ​ 随便说明一个元素的意义，以D的第一行第二列元素(-1, 0)为例：这里说明的是：\(D\)与\(B\)的相对位置差别：B相对于D是行-1，列不变，故为(-1, 0)。那么将每个元素战平可以得到： \[ \begin{equation}\label{flat} \begin{pmatrix} (0,0) & (0,1) & (1,0) & (1, 1) \\ (0,-1) & (0,0) & (1,-1) & (1, 0) \\ (-1,0) & (-1,1) & (0,0) & (0, 1) \\ (-1,-1) & (-1,0) & (0,-1) & (0, 0) \\ \end{pmatrix}\\ \end{equation} \] ​ 我在公式\(\eqref{rm}\)下面的无序列表中说到：x、y方向是等价的，故实际上公式\(\eqref{flat}\)中不同的相对坐标值可以简化：比如我们从左下角开始标记id，相同的相对坐标值id相同，可以将公式\(\eqref{flat}\)标记为（标记不唯一）： \[ \begin{equation}\label{id} \begin{pmatrix} 4 & 5 & 7 & 8 \\ 2 & 4 & 6 & 7 \\ 1 & 3 & 4 & 5 \\ 0 & 1 & 2 & 4 \\ \end{pmatrix}\\, \begin{pmatrix} 3 & 4 & 5 & 6 \\ 2 & 3 & 4 & 5 \\ 1 & 2 & 3 & 4 \\ 0 & 1 & 3 & 4 \\ \end{pmatrix}\\ \end{equation} \] ​ 我们可以：

• 在一个表中预存不同id对应的bias
• 将这个表变成learnable的，每次索引就好了，让网络自己学值

​ 公式\(\eqref{id}\)看起来真的很像绝对位置编码的样子，事实上这里就体现了绝对位置编码和相对位置编码的共同性以及相互转化。就像相对位姿一样，只要与一个global项（绝对量）结合，相对就会转化成绝对，反之亦然。

​ 值得一提的是：对于window size为L的window来说，因为每个像素点在不同方向上最多有\(2L-1\)个不同位置，那么(x, y)的相对位置组合也就有\((2L-1)^2\)种情况。比如，公式\(\eqref{id}\)对应L=2的情况，就有9种不同的位置，L=3时为49种... 等等，都是可以验证的。理解了这个，indexing机制就只剩一个问题了：怎么实现。这个... 也不能完全说是问题吧。

​ 我在某天午夜思考实现方法，想了一小时没有头绪，遂睡觉。第二天早上醒来在床上花了三分钟想到了实现方法，这告诉我们睡眠非常重要。实现思想非常简单，所有其他位置的index，都可以复用(0, 0)位置的index，并在(0, 0)位置的index表元素中加上相同的偏置就可以了。

​ 关于2D relative positional bias，还有一个问题就是：positional bias的shape应该如何？

当然是\((\text{head num}, 2L-1,2L-1)\)

​ 但是为什么是这样呢？

​ 首先，relative positional bias之所以与embedding dimension一点关系都没有，是因为人家叫 bias，学的内容并不是一个什么向量，它就是一个在计算softmax时加入的偏置，是一维的，并且每个head是不一样的。

​ 其次，为什么是一个大小为\(2L-1\)的方阵呢？因为两个方向都有\(2L-1\)种不同的位置。

---

IV. 复现结果

​ swin transformer针对的是大型数据集（ImageNet），显然，这是我电脑没办法带动的（实验室的单3060也没办法跑）。所以我找了一些"compact ImageNet"，最后选定的是imagenette2-320（与timm docs使用同一个数据集）。数据集中图像的高固定为320。数据集共有十个分类，每个分类大约1000张图片（很小了）。

收音机	卡车	鱼

Figure 6. 一些分类图片（相比之下CIFAR-10就是高糊）

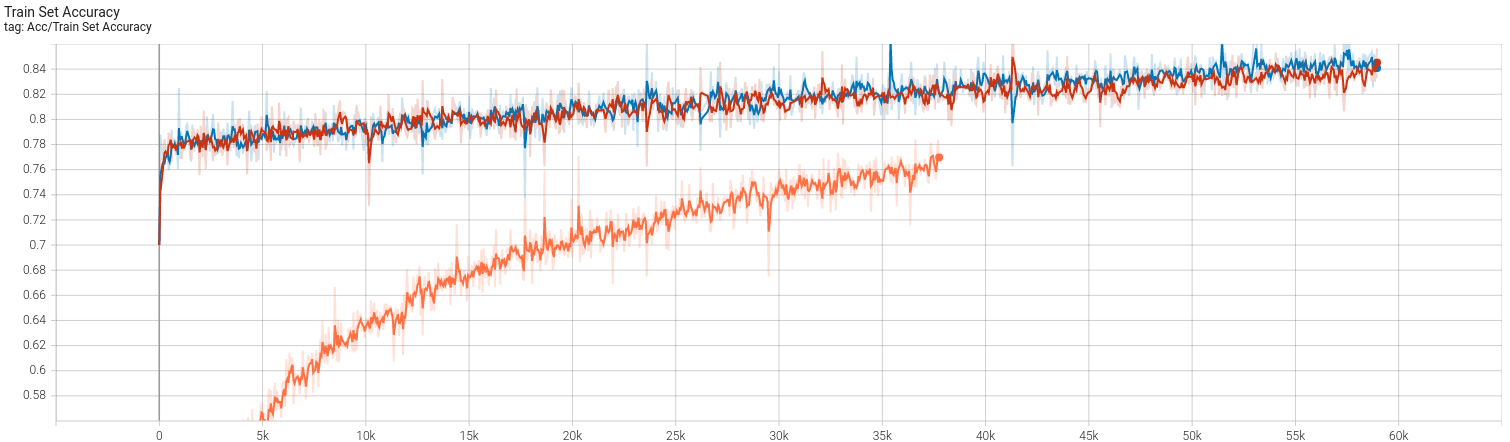
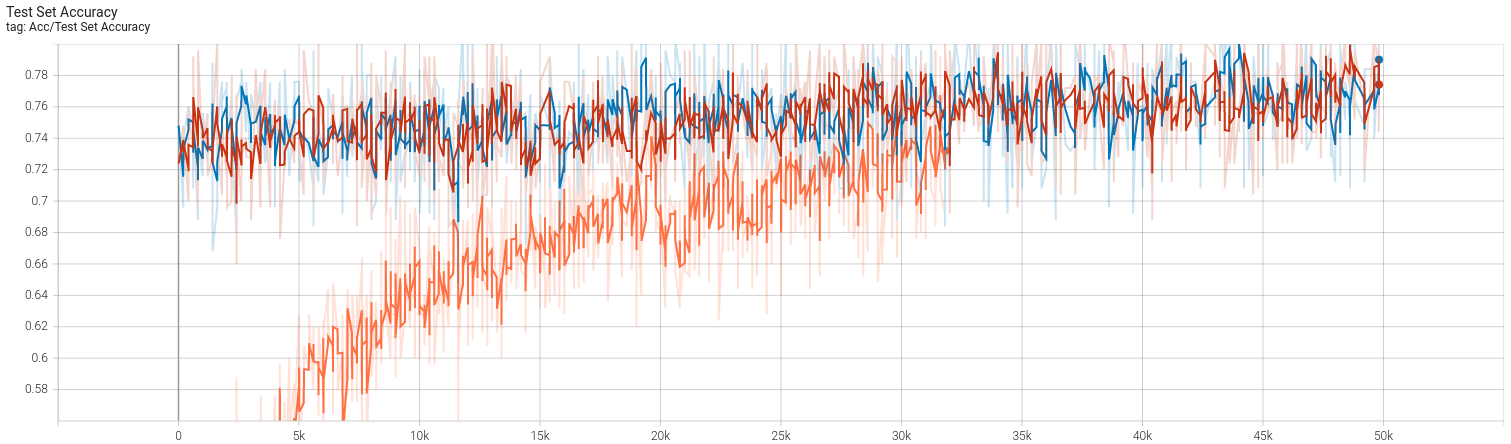
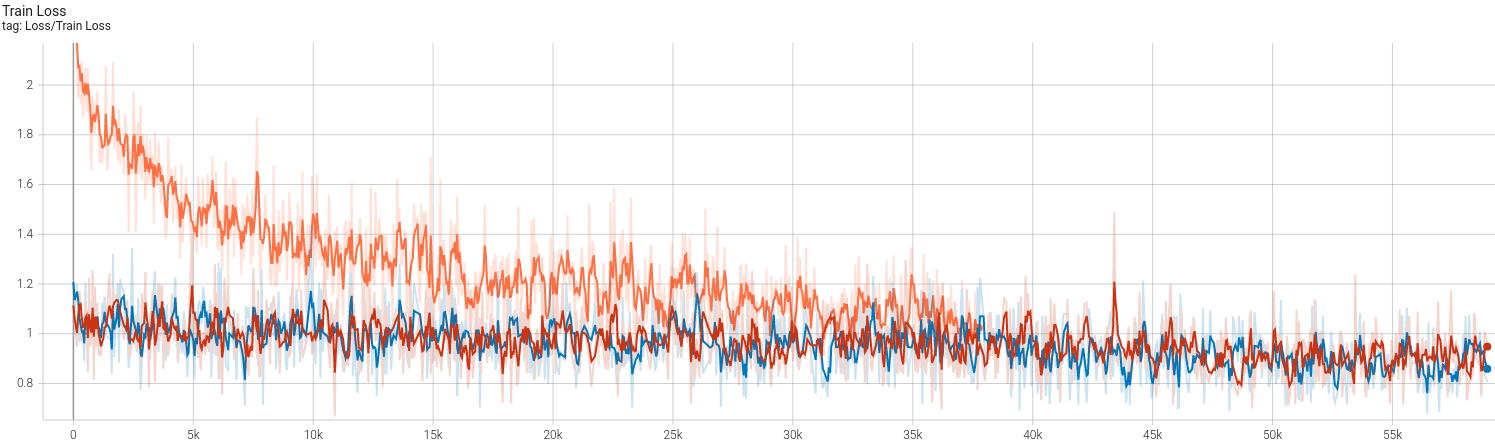
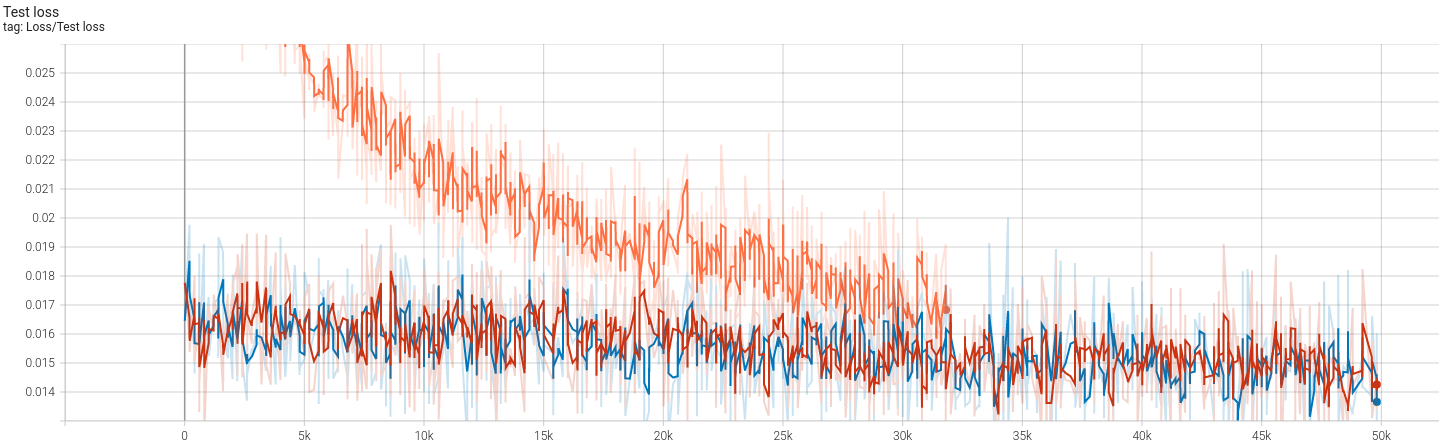
​ 不得不说，224 * 224的图像确实非常吃显存。batch size为50时显存占用是10GB，再高就炸我显卡了，故最后batch size取了一个保险的40（约8GB占用）。复现结果如下：

​ 首先得说明的是，我使用的参数基本与CCT一致，并没有调过，也不想费事去调，只是想理解一下本文的思想。文中使用的现代CV训练方法，比如cutmix等等这些操作，我一概没有使用，scheduler曾经使用过timm实现的余弦退火，但是最大最小学习率设置不合适，导致训练结果直接崩了（从70%调到10%），笔者也并不想花时间调。最终的结果大概是（存在过拟合，同样笔者也懒得调优了）：

• 训练集83.5% 测试集78% (imagenette2-320)
• 除了第一次使用160 epochs之外，其余均是250 epochs，学习率固定分别固定(1e-5, 5e-6以及4e-6)

Figure 7. train set accuracy

Figure 8. test set accuracy

Figure 9. train set loss

Figure 10. test set loss

---

V. 一些torch函数

torch.triu

triu(input, diagonal=0, *, out=None) -> Tensor Returns the upper triangular part of a matrix (2-D tensor) or batch of matrices

​ 也即可以通过这个函数获得某个矩阵的上三角部分。对应的下三角是torch.tril。其中的diagonal参数指示了：相对于真正的对角线的偏移量，默认为0，也即对角线下方的所有元素设为0。如果是正数，比如1，将会使得0元素分界线向右上方偏移（1），反之往左下方。不是很常用。

torch.masked_fill

​ 本实现中使用了此函数：在attention mask中，将所有为负数的区域变为-100（使得logit很小）。传入的第一个参数相当于条件张量（一般会转化成true false的bool张量），第二个参数是需要fill的值。

torch.gather

​ 本实现中，relative positional bias一开始的实现使用过。gather实际上在没有view改变形状的情况下，直接根据提供的index，在原始矩阵中进行索引，得到的值组成一个新的矩阵：

rpe = torch.gather(s, -1, self.relp_indices.repeat(batch_size, win_num, self.head_num, 1, 1))

​ 上公式可以直接在最后一维度选择（第二个参数，dim = -1），直接根据索引(self.relp_indices)，从一个（最后两个维度）shape为(2L - 1, 2L-1)的矩阵中直接取出一个大小为(L, L)的矩阵。

torch.register_buffer

​ torch有两个常用的 与 "register" 有关的函数：register_buffer以及register_parameter

• register_buffer会将对应的张量加入到model.state_dict中，但是它不会参与反向传播计算。这给我们保存模型中一些无关参数（或者常数）提供了便利，这样加入model.state_dict中的参数可以直接被torch.save保存

torch.view / torch.reshape / torch.contiguous

help(torch.reshape): Contiguous inputs and inputs with compatible strides can be reshaped without copying, but you should not depend on the copying vs. viewing behavior.

​ view只能针对contiguous的数据进行操作，是在底层数据内存组织基础上，返回一种以不同于底层数据内存组织方式的视角（view，或认为是步长）来查看数据的tensor。比如：底层是矩阵\(A_{2\times2}\)，transpose之后是\(B_{2\times2}\) \[ \begin{equation} A=\begin{pmatrix} 1 & 2\\ 3 & 4 \end{pmatrix}, B=\begin{pmatrix} 1 & 3\\ 2 & 4 \end{pmatrix} \end{equation} \] ​ A在内存中实际上是按照行优先进行一维存储的：实际上保存的数据是(1, 2, 3, 4)并且按照stride = (2, 1)进行访问。而B作为A的transpose，实际上没有修改内存组织（transpose后的数据与A共用内存（如果不小心可能会导致不想要的修改）），但是是以stride = (1, 2) 访问数据。这里的stride = (i, j)可以认为是：

• 行方向上的索引增加1，在物理地址的寻址中需要移动i个位置
• 列方向上索引增加1，物理地址寻址需要移动j个位置

​ 故由于B是(1, 2)，那么B[0, 1] = (B基地址 + 1 * 2偏移).value = 3。B[1, 0] = (B基地址 + 1 * 1偏移).value = 2。

​ 上示例中，A是contiguous的，但B并不是，因为其访问数据的方式在内存中不是线性连续的。故B这样的矩阵，不能直接view

• 直接view操作不改变内存组织方式，view前后数据共享内存
• reshape相当于是 X.contiguous().view。如果一个矩阵不是contiguous的，contiguous操作将会开辟新的内存空间并复制原来的tensor，以新的view进行数据存储
• 值得一提的是，permute, narrow, expand, transpose操作之后，均会使得contiguous不成立。但是view操作过后，虽然stride可能发生改变，但其并不影响contiguous性。

---

Reference

[1] Github: microsoft/Swin-Transformer

[2] Huang, Cheng-Zhi Anna, et al. "Music transformer." arXiv preprint arXiv:1809.04281 (2018).

[3] AI Summer:How Positional Embeddings work in Self-Attention (code in Pytorch)