Depth Completion论文三篇
Depth Completion
I. Intros
深度补全中存在多模态数据融合的问题:单目RGB图像直接进行深度估计比较困难(直接深度估计,个人感觉只能凭借常识和先验知识),而如果同时存在稀疏激光点云(散步在稠密的图像上),可以通过“传播的思想”将一些位置的深度传播出去。在返乡的高铁上没事干(事实上由于河南大雪以及湖北大雨,高铁变成了低铁,时间+2h),看了五篇论文,本文简要分析了其中三篇关于 guided深度补全的文章:
- ICCV 2019: Xu, Yan, et al. "Depth completion from sparse lidar data with depth-normal constraints." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019.
- ICRA 2020 (可能写得不行 才6引): Hu, Mu, et al. "Towards Precise and Efficient Image Guided Depth Completion." arXiv e-prints (2021): arXiv-2103.
- AAAI 2020: Cheng, Xinjing, et al. "Cspn++: Learning context and resource aware convolutional spatial propagation networks for depth completion." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 34. No. 07. 2020.
本文可能写得很烂,笔者在看这三篇论文以及写博客时,由于返乡安排太紧,只睡了3.25小时。
1.1 需要解决的问题
这里我就直接摘抄CSPN++中对于深度补全预期效果的阐述:
CSPN claims three important properties should be considered for the depth completion task, 1) depth preservation, where the depth value at sparse points should be maintained, 2) structure alignment, where the detailed structures, such as edges and object boundaries in estimated depth map, should be aligned with the given image, and 3) transition smoothness, where the depth transition between sparse points and their neighborhoods should be smooth. [1]
但实际上,阅读ICCV 2019文章之后,个人觉得可能还差了这两点:
- 符合3D约束,2D深度图能满足一些3D假设
- 正确的平滑假设:edge preserving的平滑假设(类似双边滤波的思想)
II. Sparse LiDAR Guidance (ICCV-2019)
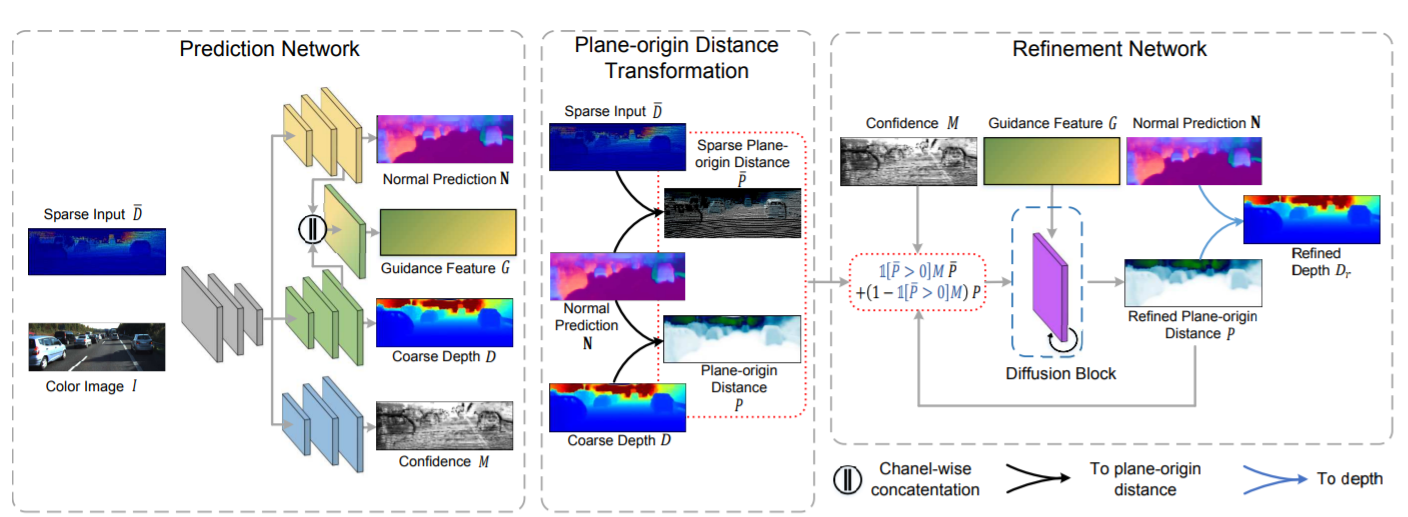
个人认为本工作虽然比ICRA-2020这篇早了一年,但是质量更高。本论文看问题的角度非常独特:
- 一般论文:直接在2D空间,硬凿loss,或者像ICRA-2020的PENet,包含一些不明所以的3D信息
- 本论文:直接在3D空间下建模 深度与法向量的关系,放弃piece-wise depth constant假设,转向piece-wise plain假设(观测由一块块平面构成)
个人认为,piece-wise depth constant是不优雅的,首先,这个假设的直接结果就是:边缘的模糊与平滑(相当于加了一个平均核),在2D CV邻域,成像结果可以是piece-wise constant的,光学成像结果不仅与深度有关,与反射率、材质、介质等等均有关系,十分复杂。但对于深度而言,此假设太过简单粗暴,而作者提到的 “plain-origin distance piece wise constant”则是基于:大量人工场景都是由碎片化的平面构成 这一特点,比较符合实际。举个例子,我们观测两堵墙,两堵墙都不是完全垂直于我们视线的。使用Piece-wise constant假设将会使得深度过渡更加平滑,对于多平面深度不连续情况而言,误差较大(会平均一些不该平均的位置),而“plain-origin distance piece-wise constant”则可以准确描述两堵墙(甚至是更多的平面)。
本论文的一般处理步骤:
特征提取网络(prediction stage)
Recurrent Refinement Stage
使用Diffusion model(类似置信传播,但并未直接使用MRF或者CRF相关公式),可以认为是一种规则的图卷积?迭代多次,diffusion根据两个像素位置对应的guidance feature相似度判定diffusion coefficient。最后的结果从plain-origin distance变换为原始的深度。
当然,如果涉及到存在sparse LiDAR深度点的像素位置,特征提取网络输出的 confidence 将会把原深度以及预测深度加权求和。
这里只简单推一推Plain-origin distance:已知点到平面的距离公式是 \[ \begin{equation}\label{dist} N(\pmb{X})\cdot \pmb{X} -P=0 \end{equation} \] 其中\(N(\pmb{X})\)是三维点\(X\)所在表面的切平面(tangent space)的法向量,通常来说,给定足够多的点,可以使用PCA或者求解协方差矩阵最小特征值对应特征向量(实际上还是类似PCA)的方法求解。\(\pmb{X}\)是平面上一点到相机中心的相机坐标系3D vector。公式\(\eqref{dist}\)表达的意义很清晰,\(N(\pmb{X})\cdot\pmb{X}\)是 \(\pmb{X}\) 在平面法向量上的投影距离,也就是原点到平面的距离。
而有深度值 + 相机内参 + 像素位置,可以根据\(zK\pmb{x}=\pmb{X}\)求的\(\pmb{X}\)。那么正逆变换: \[ \begin{align} &P(\pmb{x})=D(\pmb{x})N(\pmb{x})K\pmb{x}\\ &D(\pmb{x})=\frac{P(\pmb{x})}{N(\pmb{x})K\pmb{x}} \end{align} \] 总的来说,这篇文章很好理解,写得很清晰。
III. PENet (ICRA-2020)
PENet个人感觉创新点很有限,这个网络给人一种十分魔法的感觉,比如Color-dominant和Depth-dominant是如何进行处理的,为什么可以做到不同模态数据的dominant。
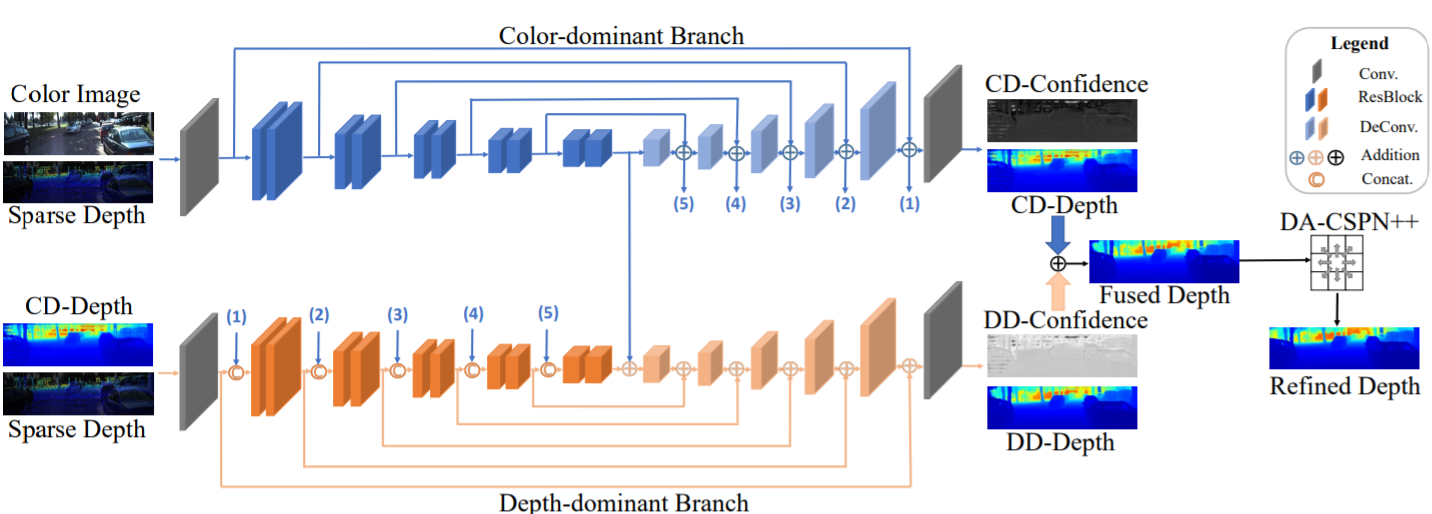
3.1 Dilated & Accelerated CSPN++
作者唯一花了大篇幅介绍的,有实质内容的部分就是这一部分。其中有个很奇怪的地方(可能是我不懂Spatial Propagation Network),其中的公式(3): \[ \begin{equation}\label{map} D_{i}^{t+1}=W_{ii}D_i^0+\Sigma_{j\in N(i)}W_{ji}D_j^t \end{equation} \] 对于这种迭代式的结构,个人感觉有点类似RNN(RAFT里就有RNN的某个经典结构:GRU)。但这和卷积的区别在哪?看起来很像卷积:对于图像某个位置的输出第t+1层卷积的输出,是上一层此位置周围邻域内所有输入线性组合的非线性映射(考虑激活函数)。关于这个translated propagation,照我个人理解,其意思大致是这样:仍以论文中\(3\times3\)邻域为例:
在一般情况下,对于一个【特征图】进行计算的\(3\times3\)矩阵实际上应该是一个张量,此张量可以是\(3\times3\times C\)大小的。换句话说,这里有9个特征向量,被组织成了二维grid结构。那么如果需要输出是一个向量,那针对每一个向量的映射就应该是大小为\(C\times C\)的矩阵。故公式\(\eqref{map}\)中定义的\(W\)实际上应该是很多矩阵。
这里与卷积不同的是:卷积层的每一个kernel都会考虑感受野内的每一个输入(除非这个卷积学习得很奇怪,就只有一个点值非0)。比如此处的\(3\times3\times
C\)的输入。假设我们使用一个Conv2d(C, N, k = 3)进行计算(输出一个大小为\(1\times1\times
N\)的向量),输出的第k个通道(此处也即\(\text{output}_{[0,0,k]}\))是: \[
\begin{equation}
N_k=\sum_{t=0}^C\left\{\sum_{i=0}^2\sum_{j=0}^2A_t(i,
j)C_t(i,j)\right\}+\text{bias},\text{ where }A\text{ is input and
}C\text{ is kernel}
\end{equation}
\] 卷积实际上是将图像以通道划分的,处理信息的视角是
通道。而此处的Spatial Propagation,是以每个像素的特征向量为视角: \[
\begin{equation}
V_o=\sum_{i=0}^2\sum_{j=0}^2W_{ij}A(i,j),\text{ where
}W_{ij}\in\R^{C\times C}
\end{equation}
\]
我们可以认为这就是一个向量的线性组合过程。综上所述,通俗地来说:
- 卷积是以通道为视角的,卷积核都是每个通道进行计算的
- Spatial propagation(至少在这篇论文里)是特征向量(某一点的所有通道值)为视角的,可以视作向量的线性组合。
但需要注意的是,以上只是个人认为的【卷积】与【SP】的区别,论文中实际以【深度图】(单通道,而不是上文所说的特征图)进行计算,故每个\(W_{ij}\)实际是一个具体的值。由于第t+1次迭代的输出(x, y)是第t次迭代输入(x, y)邻域值的组合。而由于不同像素\((x_1, y_1)\)相对于其邻域某个点(比如相对距离(-1, -1)的像素)与\((x_2, y_2)\)相对于相同的相对位置点,affinity值是不一样的,权重并不是共享的,故简单卷积是无法计算的。
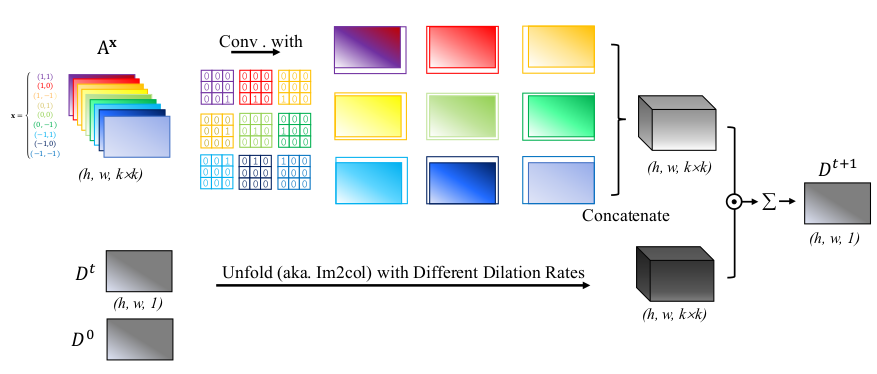
事实上,按照SP的思想,每个像素相对于邻域内某个相对位置点将得到一affinity值,那么对于某一个相对位置点,将得到一个大小为\((H, W)\)的单通道affinity map,就比如:,图像中所有像素相对于\(3\times 3\)邻域内(-1, -1)位置将形成一个单通道affinity map,那么\(3\times 3\)邻域将形成9个相对于不同位置的单通道affinity map。而且这些affinity map就像是relative positional embeddings一样,需要与正确相对位置的值运算,举例说明:
- 考虑图像上(1, 1)点对应的像素,并考虑一个\(3\times 3\)邻域
- (1, 1)点对应像素在迭代生成输出时首先应将自身值与【相对位置(0, 0)的affinity map通道】上的【(1, 1)位置值(代表了(1, 1)点相对于与自身相对距离为(0, 0)点的affinity)】进行相乘,作为base值
- 后(1, 1)点计算其领域点信息:
- (0, 0)点相对于【(-1, -1)affinity map通道上的(1, 1)位置】值相乘,叠加到base值上
- (0, 1)点相对于【(-1, 0)affinity map通道上的(1, 1)位置】值相乘,叠加到base值上..., etc.
- 从Figure 2中也看出相应的意思:\(A^x\)是不同方向(x为方向,也即相对位置)对应的affinity map,在经过one-hot convolution之后,组成一个乘法kernel。
显然我们是不希望使用for循环的(对于CUDA加速不友好)。作者的方法实际上就是使用one-hot convolution实现了tensor的roll操作,并且此roll不是循环的(设0),因为有些像素就是没有某个特定位置的值(比如右下角点没有(1, 1)相对位置点)。直接roll可能需要借助额外的masking操作,故作者就使用固定的one-hot卷积核,卷积affinity map的每一个通道(每个通道的one-hot 卷积核不一样,因为所表示的相对位置不一样),卷积的结果可以直接用于【乘法 + 叠加】操作。
IV. CSPN++ (AAAI-2020)
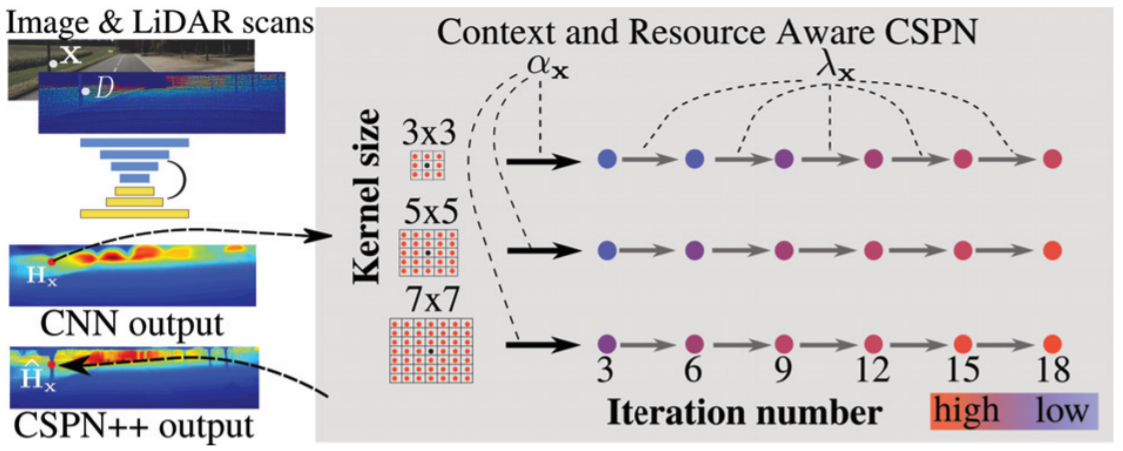
本论文可以称为是:终极自适应 工作。CSPN++在两方面进行了自适应考虑:
- Context-aware:对于图像内容本身的处理进行自适应,用以提升精度
- Resouce-aware:对于计算资源的自适应,比如自适应选择 卷积核大小(或propagation域大小) 以及 迭代次数(per-pixel)
两方面的awareness存在权衡关系:计算资源富足时在计算精度以及结果质量上必然更好,反之亦然。其中,个人觉得Context-aware没有特别多可以说的,作者也就是从两个不同的角度进行信息综合:
- 每一个像素使用不同大小的kernel得到的结果综合
- 每一个像素迭代不同阶段时的信息综合
CSPN block迭代公式本身是: \[ \begin{equation} H^+_x(t+1)=\kappa(x) H_x(0) + \sum_{y\in N(x)}\kappa(y)H_y(t),\text{ where }N(x) \text{ is the neighbor of }x \end{equation} \] 其中的neighbor表示去心邻域,以上操作记为\(H_{CSPN}(x,t)\)
综合 迭代平均 以及 核平均,更新公式应该是(我们令\(H_x(t )\)为迭代第t次时,像素位置x的深度值hidden state): \[ \begin{align} & H^+_x(t+1)=\lambda_x(k, t+1)H_{CSPN}(x,t)+H^+_x(t)\\ & H^+_x(t)=\sum_{i=0}^k\alpha_x(k)H^+_x(t,i), \text{ where }H_x^+(t, i) \text{ also indicates kernel size} \end{align} \] 其中\(\lambda_x(k, t)\)(迭代综合系数)以及\(\alpha_x(k)\) (kernel综合系数)都是网络的输出,注意这些系数均带有下标,说明是与像素有关的 per-pixel prediction coefficient。
本论文有意思的点在于,论文通过Context-aware propagation过程定义的公式,导出了computational cost的简单表达式,computational cost在此处的作用相当于惩罚项。由于Context aware的过程是:multi-branch prediction,最后根据预测的\(\alpha\) 以及 \(\lambda\)系数整合多branch的预测结果。此处,\(\alpha\)以及\(\lambda\)是先于CSPN block实际迭代过程给出的(由一个修改的ResNet-34网络给出)。在Resource-aware计算过程中,作者将 “weighted average”变为了“max pool”:根据预测系数,每个像素位置选择“最大”branch进行计算: \[ \begin{equation} k_x^*=\mathop{\arg\max \alpha_x(k)}_k,t^*_x=\mathop{\arg \max\lambda(k_x^*,t)}_t \end{equation} \] 这样可以省去多路计算的计算开销,但显然这样牺牲了结果质量。
另一方面,作者在论文中对computational cost进行了建模: \[ \begin{align} & E(c_x|\{\alpha_x, \lambda_x\})=\frac 1{hw}\sum_x E(c_x|\alpha_x, \lambda_x)\label{normx}\\ &E(c_x|\alpha_x, \lambda_{x})=\frac 1 {Nk_{\max}}\sum_{k}\sum_t\alpha_x(k)\lambda_x(k,t)k^2t\label{norma} \end{align} \] \(\eqref{normx}\)相当于是所有像素位置求平均(期望),\(\eqref{norma}\)则是某一个确定的像素位置进行的期望计算:因为一个像素位置进行传播的复杂度显然是\(O(k_{\max}^2N)\),其中\(k_{\max}\)是最大核大小,\(N\)是迭代次数,而如果将\(\alpha\)以及\(\lambda\)分别看作核取大小 \(k\) 以及 迭代次数为 \(t\) 时的概率(个人认为这是可以的,在“max pool”下选取的就是最大“概率”branch进行计算),cost的期望便可以以上述两个公式进行计算。
事实上作者也将此惩罚项向有约束优化中拓展了,但最后的形式还是惩罚项(因为这个优化问题non-convex,拉格朗日对偶没啥大用处)。惩罚项的坏处就是,约束是软约束,超出约束范围是可能的。
不过综上所述,个人觉得CSPN++这篇论文相对还是比较有意思的(尤其是Resource-aware部分),有一定启发性,相比ICRA 2020的PENet,个人觉得这篇文章写的更不那么魔法。