Instant Neural Graphics Primitives
Instant NGP
I. Intros
保研前是想搞3D重建来着,大概是无缘吧(xD)。最近老被安利 【5s NeRF训练】,听起来很强的样子,速度提升了好几个数量级,遂观摩了一下:
文章很有趣,对我现有工作有一定的启发价值,当然结果也很nice:

II. 简单分析
2.1 本文在解决什么问题
本领域我了解很少,在搞2D SLAM时了解过一些SLAM对地图的建模方式。其中有一个方式叫做隐式函数(implicit functions),旨在用一个参数化的函数来表示一个曲面。而当下神经网络应用火爆,这种参数化的表面表征当然可以使用深度学习的方式来学习。比如如下两篇论文所说的:
Neural SDFs are typically encoded using large, fixed-size MLPs which are expensive to render.[1]
Our algorithm represents a scene using a fully-connected (non-convolutional) deep network, whose input is a single continuous 5D coordinate (spatial location (x, y, z) and viewing direction (θ, φ)) and whose output is the volume density and view dependent emitted radiance at that spatial location.[2]
最容易理解的例子应该就是SDF(有向距离场),之前也做过有向距离场表示的点云融合。有向距离场的0集(0-水平集)代表了真实曲面,而有向距离场就是给定一个d维输入(d维空间中的一点),输出正负值(在d-1维流形的“内部”还是“外部”)。那么这个d-1维流形(高维曲面)可以使用神经网络来表示,毕竟神经网络是万能的函数逼近器。如上引用所说,可以使用一个MLP(多层感知机)来“拟合”这个SDF。
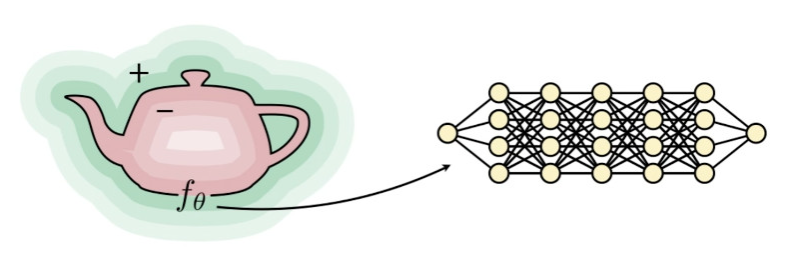
但在3D重建领域,训练这个神经网络表征可能非常困难,首先是因为数据的维度比较高,此外是输入量较大。举个例子:NeRF(Neural Radiance Field)需要一个物体的多角度输入图像,两张不同图象上对应的不同像素,可能就是两条不同的光线,需要通过已知的相机位姿 + 由内参确定的光线方向求解交点以求解真实的3D点,这一步计算量已经很大了(但按照个人的理解,这一步应该是与神经网络无关的),下一步又需要把真实的3D点与不同角度下的2D点联系起来,训练【5D输入:相机中心位置 + 本图像某一像素点对应的光线两轴角度(没有roll所以是两轴)】->【5D输出:density(相当于alpha通道)+ view-dependent RGB】的这样一个网络。如果直接把点值输入,希望在某一个小范围上直接端到端,那可能需要很深的MLP层数才能学到足够好的神经网络近似表征,这样的MLP,一是大,二是 fixed-size and task dependent,既不好训练又没有普适性。
而作者在related
work中举了一个例子:attention机制中为位置信息引入的positional
embeddings可以使得网络很好地使用(甚至学出)位置信息。把我们的低维信息embed到某个高维空间,使得我们需要训练的MLP输入不再是原始的或者简单处理的数据,而是一个个高维空间中具有良好性质(比如
可插值,n阶连续等等)的encoding,对缩减MLP大小非常有好处。反观attention机制中的一些learnable
positional
embeddings,他们的实现也不过就是(以torch为例)nn.Parameter,并没有说让输入过一些新的层,以一种不额外延长forward
pass长度的方式增加了参数数量。
不过实际上,用参数embeddings表示的情况有人已经做过了。举个例子,假设我有一个voxel map,大小为\(L\times W\times H\),voxel map中每一个点我都会有一个高维encoding。但作者也说,这存在三个很大的问题:
Memory footprint. 如果只用这样的方式设计,内存开销将会是\(O(n^3)\),这还是非常大的,很容易炸显存。
Trade-off并不值得。如果使用过量的embeddings,很可能出现:整个feature embeddings 参数块只更新一小部分参数:比如如果是2D地图上的query,在双线性插值的情况下需要取周围四个feature vectors,更新四个feature vectors,但MLP的反向传播还是会改动整个MLP的所有参数,花大力气就优化了小部分encodings,可能不值。
稀疏化也不好做。首先,稀疏化是必要的。拿另一个领域(SLAM)中的一个例子来说:占用栅格图,对于没有物体的地方我真的有必要存吗?显然我只需要存障碍物栅格即可。但稀疏化可能很困难,比如用hash方法,可能哈希冲突啊,怎么解决?链表?存到别的位置的冲突处理?这非常不利于GPU并行加速。
2.2 Multiresolution Grid
个人感觉视角合成或3D重建与双目匹配、光流类似问题还是有很大区别的,而在后两者中,一种常用的处理办法就是特征金字塔(feature pyramid),其一般目的很简单:在特征金字塔趋于顶端位置(多次下采样后),可以进行粗匹配,粗匹配可以给向下不断扩大的精细特征图提供初值,使之更容易收敛到正确的位置(初值估计)。而视角合成与3D重建中,应该没有这种说法。个人倾向于这样认为:
- 考虑一个一般一维信号,此信号可以进行频谱分解,存在不同频率成分
- 如果我们把低分辨率(coarse部分)当作低频部分,此部分可以大致刻画局部趋势
- 把高分辨率部分(fine)当作高频部分,此部分可以刻画局部细节
- 就比如一座山峰,其整体趋势由低频决定,而山峰上的各种崎岖地形由高频 部分决定
也即,multi-resolution grids是为了兼顾不同方面(低分辨率局部趋势)(高分辨率局部细节)而设置的结构。而作者在此处的设计是这样的:

作者并没有使用稠密的grid结构,稠密的特征grid开销太大了(所以RAFT搞的full correlation volume到底在干什么),作者在不同的分辨率层级上射击了双射或满射(应该是满射吧),也即 \(f:R^2\rightarrow R\):
- 在低分辨率层级上,由于grid数量本来就较少,那么每个grid足够分配到一个特征向量
- 在高分辨率层级上,grid数量多,为了不\(O(N^2)\)复杂度增加特征向量,将根据分辨率线性增加特征向量数目,此时可能引发 哈希冲突。
而暴力划分grid,重建精度将会收到grid分辨率影响,作者直接使用临近点线性插值的方式获得更加“精细”的特征,可插值性在本问题中非常有意义,如果在同一个grid(四个角点对应相同的特征向量index)中两个不同点特征向量在网络输出上并没有平滑性,那么将会使学习到的函数(比如SDF或者radiance field)不连续,0阶不连续代表着表面连接特性的跳变,在与深度视觉相关的邻域中,0阶不连续是可以容忍的(毕竟存在不同位置的物体以及遮挡),而在单个物体表面重建或视角合成中将导致结果有问题。至于为什么此结构具有可插值性,我将在后文分析。
最后不同分辨率的特征将被concat在一起。用concat的理由:
First, it allows for independent, fully parallel processing of each resolution. Second, a reduction of the dimensionality of the encoded result y from LF to F may be too small to encode useful information. (要知道F才2)
2.3 哈希冲突
作者说自己并不显式处理哈希冲突,因为哈希冲突的解决涉及到较为复杂的逻辑(并且判断是显著增了)。我们知道,在一个wrap中存在逻辑分支,将会引起wrap divergence,对于if/else同等计算量需求的操作,将损失至少50%的计算速度。但不解决哈希冲突将导致 两个不相的grid(甚至可能物理距离就很远)映射到同一个特征向量上(hash出来的index是一致的),理论上来说,这将对反向传播过程产生影响(一个特征向量同时在多个不相关的位置贡献loss)。而实际情况中没有影响主要有这么三个原因:
Multi-resolution 结构。我们已经提到,(1)低分辨率决定了局部趋势(2)低分辨率足够双射。这样一来,低分辨率决定的局部趋势就可以保证正确性。此外,所有可能产生哈希冲突的分辨率层级同时产生哈希冲突是“statistically very unlikely to occur simultaneously”,那么我们就应该看高分辨率下哈希冲突时具体的学习过程。
【这部分我感觉作者有点强行解释】:梯度加权平均。作者认为,即使两个不关联点A,B拥有同一个特征向量,A,B最终贡献给loss的大小也几乎不可能相同。比如A接近物体表面,B在empty space中,那么最后loss很可能会更倾向于给A更大的权重,造成:同样一个特征向量产生的两份不同梯度,A的梯度方向占主导地位。最后网络也会自行向与A相关的方向优化。
但若考虑到产生多次哈希冲突的情况,个人觉得很有可能产生哈希冲突的这些点各自可能的权重 也随机散布在空间中,那最后合成出来的梯度实际上是个四不像梯度... 还是有可能产生奇怪输出的,只不过“statistically very unlikely to occur”罢了。于其说是:“implicit hash collision resolution”,不如说是:我发现不解决哈希冲突本来就基本不可能有啥问题。我个人对这种处理方法的看法是:“mostly elegant, statistically unlikely to be inelegant”。
2.4 可插值性与平滑性
笔者已经在上文解释过了,可插值性是非常重要的。但本设计为什么会存在这种可插值性?有如下几个疑问:
- 此设计是天然具有可插值性(就像CNN的平移不变性以及transformer的置换不变性)还是需要靠其他人为步骤的设计使其具有可插值性?
- 如果是后者,这种奇妙功能是如何实现的?
- 如果不仅仅需要连续,还需要可导的平滑表面,应该怎么做?
作者说:
Interpolating the queried hash table entries ensures that the encoding enc(x; θ), and by the chain rule its composition with the neural network m(enc(x; θ); Φ), are continuous.
也就是说,multi-resolution hash table 本身是没有可插值性的,正是因为我的插值操作使得网络具有了可插值性【Counter-intuitive】。为什么会这样呢?
对于低分辨率层级来说,可能很多输入点都落于一个grid(或者voxel)内部,这时这些点将会共用grid(或者voxel)的角点index,也就是插值所使用的特征向量索引。由于可以认为,输入点在空间上临近,输出结果也要求需要在空间上临近。举一个这样的例子,假设我需要根据2D图像恢复3D模型,那么2D输入点临近对于一个原本连续的形体,应该就是连续的(对于原本就是不连续的形体则另说)。那么,网络根据A,B,C几个点插值后的特征的相似性,结合输出结果在监督下的ground truth相似性,就能推出此局部是否应该具有可插值性:
- 临近输入导致临近以及相似输出 --- 说明是可插值的,映射函数连续
- 临近输入导致结果差别大或者不相似 --- 说明局部不可插值(可能分属不同物体或者是一个物体的几个分立子原件),允许映射函数不连续
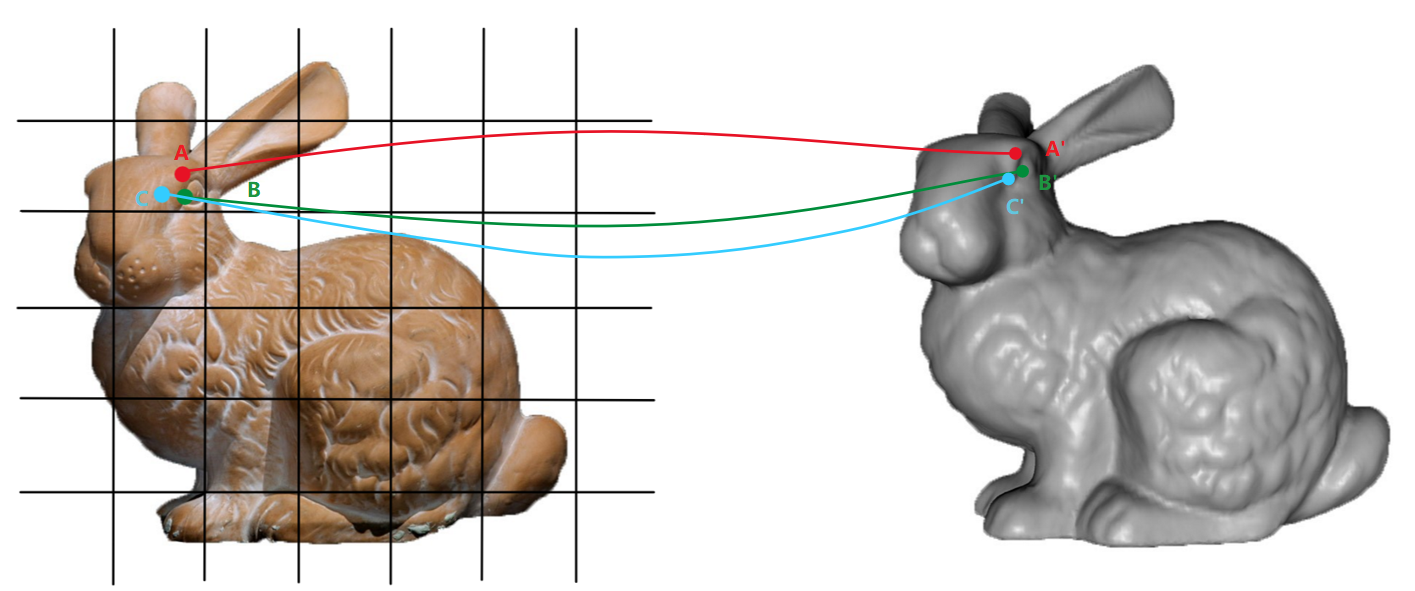
学习连续性还是较为简单的,只需要设置相应的监督【相似/近输入】--> 【相似/近输出】。而对于高阶平滑,比如SDF就要求一阶(导)连续(代表着可导)作者说有如下两种方法:
双二次以及双三次插值可以使得导数不再是呈块状的,而是连续的。但是需要的lookup成本变高了,就拿双三次插值来说,双三次插值需要一次采样16个点的特征向量,而双线性只需要四个点,放在3维空间中开销更加难以接受。
\[ \begin{align} &S(x)=x^2(3-2x)\\ &S'(x)=6x(1-x) \end{align} \] 作者推荐这样的插值公式,在双(三)线性情况下只采样4(8)个点,又可以:
The derivative of the smoothstep vanishes at 0 and at 1, causing the discontinuity in the derivatives of the encoding to vanish by the chain rule.
意思是:导数在0,1(也就是插值边界处)为0,根据链式求导的导数相乘,使得边界点的导数为0。也即不会因为线性插值这样在边界出现导数不连续的情况。感觉有点妙。
III. 其他后续
笔者近几天回到家没有可用设备来训练,想试试demo但没有办法。笔者之后可能写一篇本文官方实现的源码分析,暂定应该是《CUDA踩坑实录【4】》的内容。