我贫瘠的数学世界【1】- SAM与优化方法
BFGSAM
I. Intros
很长一段时间没有静下心来看过有很强理论性的内容了,我十分担心自己会丧失理论上的思考能力以及数学计算能力。正好之前在看某篇论文时,看到其中提到一种叫做SAM(sharpness aware minimization)的方法,说是效果还行,此前保存了SAM论文,但没去细读。最近寒假由于电脑故障没办法工作,很闲,便重新了解了一些数值优化方面的知识(比如拟牛顿族),并读了读SAM(虽然读完感觉???这怎么这么魔法)
- ICLR 2021: Foret, Pierre, et al. "Sharpness-aware minimization for efficiently improving generalization." arXiv preprint arXiv:2010.01412 (2020).
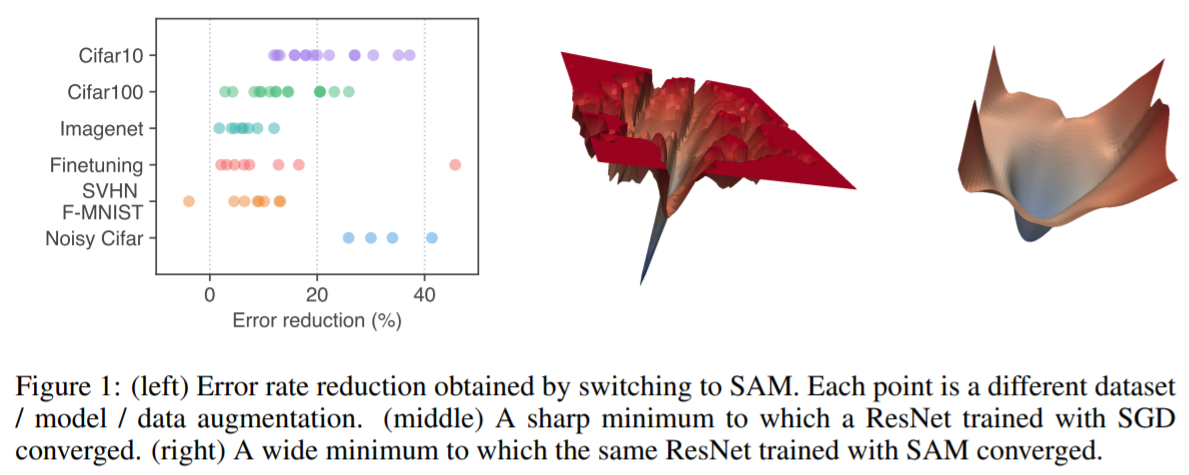
- 《我这种菜鸡哪有资格觉得DL顶会论文魔法》系列(下图图源论文)
II. 条件数与quasi-Newton
2.1 条件数与稳定性
条件数(condition number):
The condition number of a function measures how much the output value of the function can change for a small change in the input argument.
这个概念也就是一个衡量输入输出关系的指标:输入发生小的改变是否会使得输出发生大的改变?如果会,那么优化结果将有很大的抖动。比如在深度学习中,观察loss曲线,loss波动非常大,可能因为条件数太大,需要使得输入的变化在合理范围内减小(控制学习率)。
这里我们不对一般的优化问题进行讨论,只讨论矩阵情况。矩阵中,条件数是: \[ \begin{equation} \kappa(A)=\frac {\sigma_{\max}(A)}{\sigma_{\min}(A)} \end{equation} \] 其中\(\sigma_{\max}\)代表矩阵A的最大奇异值(如果是非奇异矩阵,就是最大特征值),\(\sigma_{\min}\)是最小特征值。经常我们在奇异值分解时,取出其对角值,判定最大特征值与最小特征值之比,如果过大就进行一些保护操作,实际上就是在保护大条件数时的解情况。
条件数确定了一个问题的前后向稳定性:
算法的“前向误差”是结果与真解之间的差别,即\(\Delta y=y^{*}-y\)。“后向误差”是满足\(f(x+\Delta x)=y^{*}\)的最小\(\Delta x\),也就是说后向误差说明算法的所解决的问题。前向误差和后向误差通过条件数发生关系:前向误差的幅度最多是条件数乘以后向误差的幅度。[2]
2.2 Preconditioning
假设我们已经知道,某个问题的条件数很大(ill-conditioned),但我们又不得不解这个问题,应该怎么办?使用preconditioner(怎么翻译,不知道,日语翻译是“前処理行列”,好吧人家都是中文)
In mathematics, preconditioning is the application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solving methods.[3]
此处简单翻译一下英文维基(因为没有中文,而英文讲得挺清楚的):
- 首先假设我们有一个病态线性问题:
\[ \begin{equation} Ax=b \end{equation} \]
- 可以用一个 preconditioner矩阵 \(P\) 使得\(P^{-1}A\)使得条件数小于A:
\[ \begin{equation} AP^{-1}(Px)=b \end{equation} \]
- 我们认为:\(AP^{-1}\)是一个新的矩阵\(Q\),也就得到:\(Qy=b\)这个问题,首先解这个问题得到\(y\)后再根据\(Px=y\)解出\(x\)
很巧妙的方法。进一步了解这种方法的应用以及其work的机制,参见reference。
2.3 Quasi-Newton法简介
拟牛顿(quasi-Newton)法,顾名思义就是牛顿法的近似。牛顿法需要用到二阶导,在更加一般的情况下---海森(Hessian)阵。但并不是所有函数都容易求二阶导,要么是因为其解析表达式太复杂,要么是因为维度太高,二阶导的时空开销都是至少\(O(n^2)\)的。此时我们可以使用一些方法来近似海森矩阵,用近似的海森矩阵计算更新方向。在此我将简介一些更为熟知的拟牛顿迭代方法(的好处):BFGS(族),DFP,SR1。
BFGS(四个人名字貌似)是一种很好用的拟牛顿迭代算法,相比于DFP以及SR1,这个算法可能有一定优势(要不然为什么Google ceres solver里的线搜索只提供LBFGS以及BFGS?难不成因为写起来简单?),并且其存在一种对内存以及算力更加友好的实现(Limited-BFGS),这个更友好的实现可以摆脱普通BFGS的\(O(n^2)\)时间复杂度,使得时间复杂度变为\(O(mn)\),一般来说m都小于n。
- 维持对称正定性。(2) 一种奇妙的自我矫正能力。(3) 对于大型稀疏问题非常有效
BFGS is the most effective quasi-Newton correction... Also, BFGS has self-correcting properties: if \(H_k\) incorrectly approximates the curvature of the objective function and this estimate slows down the iteration, then the (inverse) Hessian approximation will tend to correct itself in the next few steps. [4]
- 第一个提出的quasi-Newton方法,是BFGS update的对偶。(2)在解决二次问题时,迭代产生共轭方向(与共轭梯度法重合)。(3) 对于大型问题,效率非常低。
This formula, like BFGS, is a rank 2 formula update and it has nice properties as well, however it is not as fast. It is less effective than BFGS at self-correcting of the Hessians. Likewise, DFP could fail for general nonlinear problems, it can stop at a saddle point, it is sensitive to inaccurate line searches and it’s Hessian updates are sensitive to round-off errors and other inaccuracies. [4]
SR1如其名(Symmetric Rank-1),DFP与BFGS都是秩-2算法。
- The matrices generated are very good approximations to the (inverse) Hessian matrices, often better than BFGS.
- The drawback of the method is that sometimes \((s_k − H_ky_k)^Ty_k\approx0\) and there may not be a symmetric rank one formula that satisfies the secant condition. Hence instabilities and breakdown may occur.
秩-1算法(SR-1)得到的海森矩阵可能比秩-2算法的海森矩阵更好,但是它无法保证更新矩阵的正定性,线搜索将是非精确线搜索[5](来自台湾一个叫做,国立中正大学的课件,这大学名字感觉一看就知道在纪念谁)。
2.4 BFGS法推导
中文维基的话呢,就是简单告诉你:算法就是这样,至于推导,自己推去吧。英文维基则没有过程。推导并不难(别在开始时抄错公式就行,我因为抄错公式而花了一个半小时用各种方法推而没有结果,果然努力是不值钱的,方向错了一点用都没有)。
首先,拟牛顿法都基于这一个假设:更新方向\(\pmb{p}_k\)与海森近似阵\(B_k\),梯度的关系正如牛顿法中海森梯度与更新方向的关系如下,当然,我们也可以将这里视为对梯度的preconditioning: \[ \begin{equation} B_k\pmb{p}_k=-\nabla f(x_k) \end{equation} \] 由于\(\pmb{p}_k\)只是一个方向,可将其写为\(\pmb{p}_k=\alpha(x_{k+1}-x_k)\)。注意拟牛顿条件: \[ \begin{align}\label{quasi} &f(x_k+\Delta x)\approx f(x_k)+\nabla f(x_k)\Delta x + \frac 12\Delta x^TB\Delta x\rightarrow\\ &\text{Approx linearity: }\nabla f(x_k+\Delta x) \approx \nabla f(x_k)+ B\Delta x\rightarrow\\ &B_{k+1}(x_{k+1}-x_k)=\nabla f(x_{k+1})-\nabla{f(x_k)}\\ &\text{let: } y_k=\nabla f(x_{k+1})-\nabla{f(x_k)}, s_k=x_{k+1}-x_k\\ &\text{thus, }B_{k+1}s_k=y_k\label{update} \end{align} \] 则更新\(B_k\)(或者称为correction),必须要使得\(B_{k+1}\)满足公式\(\eqref{update}\)。在BFGS中,为了满足对称且正定(positive definiteness),人为使得更新公式如下: \[ \begin{equation}\label{new} B_{k+1}=B_k+\alpha u_ku_k^T+\beta v_kv_k^T \end{equation} \] 注意其中\(u,v\)均是列向量。只要公式\(\eqref{new}\)满足更新公式\(\eqref{update}\)即可。注意公式\(\eqref{new}\)后有两个更新项,只有一个时将是秩1算法。在这里,我们就地取材,使得\(u_k=y_k,v_k=B_ks_k\)。求\(\alpha,\beta\)。
则带入公式\(\eqref{update}\),整理后可以得到: \[ \begin{align} &(B_k+\alpha u_ku_k^T+\beta v_kv_k^T)s_k=y_k\rightarrow\\ &(\alpha u_ku_k^T+\beta v_kv_k^T)s_k=y_k-B_ks_k\rightarrow\\ &(\alpha u_k^Ts_k)u_k+(\beta v_k^Ts_k)v_k=y_k-B_ks_k\rightarrow\\ &\text{for: }u_k=y_k,v_k=B_ks_k\\ &\text{let: }\alpha u_k^Ts_k=1,\beta v_k^Ts_k=-1\\ &\alpha=\frac 1{y_k^Ts_k},\beta=-\frac{1}{s^T_kB_k^Ts_k}=-\frac{1}{s^T_kB_ks_k} \end{align} \] 则可以得到更新公式。
III.SAM
这篇论文我也不是很想细讲,不知道是因为我没有深入理解还是这篇论文本身就有那么一点魔法,个人感觉此文最后得出的算法貌似很trivial。SAM(sharpness aware minimization)是一种新的误差函数,此误差函数可以提升网络的泛化能力(使得最优值附近较为平滑)。
一般的提升泛化能力方法可以分为这么几种:
限制活动参数数量:weight decay(限制部分参数的存在)、Dropout(参数随机存在)以及比较新的stochastic depth(随机扔层,多用在attention结构中)
loss方面:比如分类问题中的label smoothing loss,使得one-hot变成了 0.9或者0.8 hot,label不再是硬的,或者说是从分类问题转化为回归问题,从“数字信号学习”变为“模拟信号学习”。
数据处理方面:数据增强(传统),Random Erase,mixup/cutmix(现代数据增强)。
在loss方面,如果说label smooth算是杰出的一个泛化能力增强尝试的话,个人觉得这还是不够的。毕竟这就不优雅。本来人家猫就是猫,我能很明确告诉你这就是猫,100%概率,但label smooth偏要说这是90%的置信度,强行软化。
SAM则着重于优化网络学习结果计算的loss形状。假设我们把loss值函数看作是: \[ \begin{equation} l=L(x;\theta) \end{equation} \] 其中x是输入数据,\(\theta\)是网络参数。我们大可以将上式看作是关于\(\theta\)的函数(可以认为输入给定),那么我们希望对于任意给定输入,loss都能保持一定的平滑性,正如我们希望 超平面是存在平滑性的,以免发生过拟合。那么如何保证此“平滑性”?
首先,我们知道,根据某个xx理论 显然 不难得到 易于证明
QED。首先,作者将问题写成了这样(这里我跳过了作者抛出的一个theorem),假设我们现在已经有了一个参数\(w\)(这是个向量但我不想打\pmb{},为了方便),我们需要找一个有更强泛化能力的参数\(w^*\),那么\(w\)局部最大loss可以写为: \[
\begin{align}
&[\mathop{\max}_{|\epsilon|_2\leq\rho}L_s(w+\epsilon)-L_s(w)]+L_s(w)+\lambda\Vert
w\Vert^2\label{div}\\
& L_s^{SAM}:=\mathop{\max}_{|\epsilon|_2\leq\rho}L_s(w+\epsilon)
\end{align}
\] 其中\(\rho\)是个超参数。作者将局部最大loss拆分为\(\eqref{div}\)就是为了说明:方括号里的项实际上包含了局部变化率信息(越大说明sharpness越高),剩余部分就是plain
loss with regularizer。
作者进一步认为: \[ \begin{align} \epsilon^*(w)=\mathop{\arg\max\;}_{|\epsilon|_2\leq\rho}L_s(w+\epsilon)\mathop{\approx}^{Taylor}\mathop{\arg\max\;}_{|\epsilon|_2\leq\rho}L_s(w)+\epsilon^T\nabla_wL_s(w)=\mathop{\arg\max\;}_{|\epsilon|_2\leq\rho}\epsilon^T(w)\nabla_wL_s(w) \end{align} \]
感觉如果直接求解\(\arg\max\epsilon^T(w)\nabla_wL_s(w)\) 只是求解在对应参数点\(w\),与\(L_s\)梯度内积最大的参数偏移值。这么看来,貌似\(\epsilon\)的方向与\(\nabla L_s(w)\)一致,范数取最大值(\(\rho\))即可?作者最后确实也是这么解的: \[ \begin{equation}\label{max} \epsilon^*(w)=\rho\text{ sign}(\nabla_wL_s(w))|\nabla_wL_s(w)|^{q-1}/\left(\Vert\nabla_wL_s(w) \Vert^q_q\right)^{1/p} \end{equation} \] 作者说p=q=2是最优参数。但... 为什么要用 sgn函数?这里... 作者写复杂了。\(|...|\)是 element-wise absolute操作,sgn + |...| 相当于是先取每个元素的值,归一化后再将原来的方向加上。
由于公式\(\eqref{max}\)求出了最终的\(\epsilon\),那么我们的\(L_s^{SAM}(w)\)梯度可以求出如下,由于\(L_s^{SAM}(w)\approx L_s(w+\epsilon^*(w))\): \[ \begin{align} &\nabla_wL_s^{SAM}(w)\approx \nabla_wL_s(w+\epsilon^*(w))=\frac{d(w+\epsilon^*(w))}{dw}\nabla_w{L_s(w)}|_{w=w+\epsilon^*(w)}\rightarrow\\ =&\nabla_w{L_s(w)}|_{w=w+\epsilon^*(w)}+\left[\frac{d(\epsilon^*(w))}{dw}\nabla_w{L_s(w)}|_{w=w+\epsilon^*(w)}\right] \end{align} \] 最后,作者甚至将上式方括号内的项省略掉,直接一步: \[ \begin{equation} \nabla_wL_s^{SAM}(w)\approx \nabla_w{L_s(w)}|_{w=w+\epsilon^*(w)} \end{equation} \] 个人感觉很暴力。因为假设这样,假设在SGD背景下进行迭代,每一次将直接取负梯度方向优化,而SAM则是首先计算本参数所在位置的梯度,之后设置一临时向量,其值是梯度归一化结果乘以ρ,计算实际更新方向时,当前参数加临时向量位置evaluate得到梯度后当作方向。而ρ是个魔法参数,也不自适应,甚至我都不知道ρ是否鲁棒,是否会出现ρ“条件数大”的情况。作者相当于在此处:
每次不在参数位置获得梯度,而在参数附近的一个魔法位置获得梯度。作者的理论也很魔法,核心部分竟然是一个一阶泰勒展开的极值(内积最大值结果),作者将其说成是 dual norm problem,好家伙,一下成了泛函分析问题了,逼格++。
虽然本文引用量100+,但个人始终感觉不太对劲(很魔法),有机会将尝试一下本算法。不过按道理来说,如果这个方法很成功,就像AdamW > Adam这样,SAM一定会被Pytorch进行官方实现的,引用量比肩ResNet、transformer也说不定,可惜并没有。
个人水平实在有限,没办法读出本文的深意,也没办法从中获得启发,如果有读者对此文产生兴趣并有自己的深入理解,笔者愿意深入探讨。
Reference
[1] Wikipedia: Condition number