3D Reconstruction with Posed Mono-cam Images
Re3D
I. Intros
电脑还没到,我[#]。不得不说京东有些店是真的脑瘫,买RTX发AMD,AMD yes也别这样啊。没办法工作的情况下只能看论文,继续3D重建。3D重建有些部分与我当前工作有重合之处,我也想从中获得一些启发。本文是两篇小论文以及一本书(这本书的其中一卷)的一个小理解:
- Murez, Zak, et al. "Atlas: End-to-end 3d scene reconstruction from posed images." European Conference on Computer Vision. Springer, Cham, 2020.
- Bozic, Aljaz, et al. "Transformerfusion: Monocular rgb scene reconstruction using transformers." Advances in Neural Information Processing Systems 34 (2021)
- 书(不得不说这本... 期刊?写得真不错,CV方向的基础以及前瞻,不过是当时的前瞻了,可能也比较老): Foundations and Trends® in Computer Graphics and Vision
附注:不让我工作我就打原神。
II. 基本概念
以下内容很多都来自于[1],个人觉得此文写得很不错,逻辑清晰,易读性强。
2.1 3D重建概述
2.1.1 3D重建的基本方法
笔者认为,3D重建行业发展的理想道路应该是:
- 单目RGB-已知图像位姿的3D重建
- 双目RGB 图像位姿可以未知
实际上,可以将第二种情况视作第一种情况的特例。第二种情况只不过是将一半的图像用于双目深度计算了。在[1]中,作者认为:
The 3D reconstruction of shapes from multiple, uncalibrated images is one of the most promising 3D acquisition techniques.
但“uncalibrated mono-cam”应该说是最困难的一种,当然如果做出来了,意义也是最大的一种(用最少的先验知识以及辅助工具获得了想要的信息,这就是优雅的、低成本的好方法)。
关于视觉3D重建,[1]中提到了两种主要的方向:
graph TB A(3D Shape Extraction) B(Passive) C(Active) D(Single vantage point) E(Single vantage point) F(Multiple vantage points) G(Multiple vantage points) A-->B A-->C B-->D B-->F C-->E C-->G H(Shape from texture<br>Shape from occlusion<br>Shape from defocus<br>Shape from contour<br>Time to contact) I(Passive stereo<br>SfM<br>Shape from sillhouttes) J(Time of Flight<br>Shape from texture) K(Structed light<br>Active stereo<br>Photometric stereo) D-->H F-->I E-->J G-->K
可以认为,active方法是一种通过一些处理使得后续的复杂计算(比如correspondence search)变简单的方法。比如使用光斑进行“制导”:一个长波光源发射不可见光,另一个接收器(相当于相机)接收光。假设我们认为发射的是可见光,接收器也是一台相机,那么相当于是:相机拍摄到一个亮斑,而发射器可以认为是相机的反向模型,则“发射器-接收器”可被视作是两台相机组成的双目系统,而亮斑的存在已经帮我们标注好了correspondence。
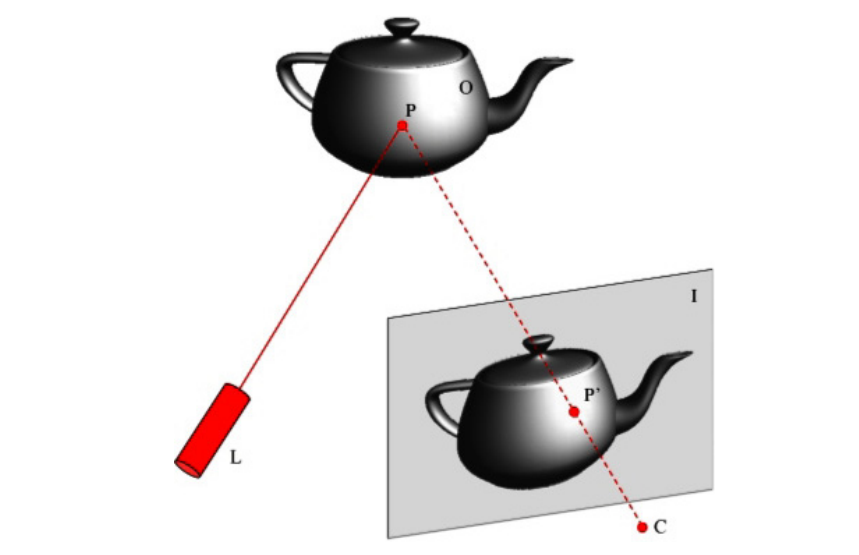
当然,单点没什么卵用。我们希望可以获得整个面的correspondences关系,是否仍然可以使用active光斑法?当然也是可行的,不过由于我们在使用单点光斑时,基于的想法是“唯一性 以及 容易查找性,直接使用单点法中光斑的2D复制显然是不行的(emmm,事实上也可以,基于红外光斑阵列的深度相机也有的,但是这种方法除了保证了极线上的全局最优性,并没有实际解决correspondence search很棘手的问题)。
[1]中作者介绍了一些对光斑进行“positional embed”的方法。比如,我就使用 Attention is all you need 中的sinusoidal positional encodings思想,用多组不同频率或者相位的正弦波来唯一地表征一个位置,这样方便我们进行查找。
本方法不使用其他辅助手段,一般来说都是直接靠算法算出结果来的。比如说:passive triangulation。通过预先计算的correspondences,解出在某一个相机坐标系下的坐标。但作者自己也说:
Correspondence search actually is the hardest part of stereo, and one would typically have to solve it for many points.
这我也没啥好说的,只能说(1)确实。(2)考虑一下CVPR 2021最新工作(好吧已经不是最新了) PointDSC?(好吧*2,作者这篇文章是2010年的)。
虽然如此,passive方法更加优雅,不依赖发射器件,只进行接收符合大多数生物的特性,并且这样的方法适用性更广,active方法对应的什么结构光、ToF一到室外场景可能就直接寄了。
2.1.2 3D重建面临的挑战
- 复杂物体形状:自遮挡 (self-occlusion),视角不全,表面细节丰富等等
- 一些奇怪的纹理:反射、透射,万花筒式(比如钻石),半透明物体
- Scalability:既要能够重建小物体,也要能够重建大物体。(从家具到城市)
- 数据量大、处理维度高(3D表征比2D高):自、弱、无监督
- 精度:这个不用讲,高精度鲁棒实时不仅仅是2D SLAM的追求
- Semantic 3D与Opportunistic scanning,说的是两个对偶:
- 前者指重建的算法过程基于内容,假设我知道我需要重建的是一辆车,那么知道“车”的先验信息或许对我进行重建有很大帮助。那么重建过程就需要对待重建的场景有一定理解,至少是语义级别的。这其中包含了一定的 High level task 帮助 low level task的意思。
- 后者指重建的数据获取过程基于内容,假设我知道当前场景大量存在无纹理区域(对passive方法不友好),我是否可以自适应更换到active方法(比如结构光)?
2.2 相机模型回顾
之前其实没有仔细推过这部分的内容,现在权当补个票。首先,我们明确一下符号:
| \(R\) | \(C\) | \(K\) | \(p\) | \(z\) | \(P\) |
|---|---|---|---|---|---|
| 外参:旋转 | 世界坐标系下相机光心 | 内参矩阵 | 图像位置 | 深度 | 世界坐标系位置 |
则若已知相机在世界系下的旋转与平移(\(R,C\)),内参矩阵已知的情况下,有如下关系: \[ \begin{equation} zp=KR^T(P-C) \end{equation} \] 实际上\(R^T(P-C)\)只不过做了一个世界系->相机系的坐标变换。此公式应当非常熟悉。
我们考虑单目已知相机位姿与参数时的情况,并且我们假设已经获得了两张图片中的correspondences(我一句话,就搞完了SLAM和correspondence search)。那么显然,对于世界坐标系下同一点: \[ \begin{align} &z_1p_1=K_1R_1^T(P-C_1)\label{first}\\ &z_2p_2=K_2R_2^T(P-C_2)\label{second} \end{align} \] 则可以通过公式\(\eqref{first}\)反求P: \[ \begin{equation} z_1R_1K_1^{-1}p_1+C_1=P \end{equation} \] 带入到公式\(\eqref{second}\)中: \[ \begin{align} &z_2p_2=K_2R_2^T(z_1R_1K_1^{-1}p_1+C_1-C_2)\rightarrow\\ &z_2p_2=z_1K_2R_2^TR_1K_1^{-1}p_1+K_2R^T_2(C_1-C_2)\label{homo1} \end{align} \] 其中\(K_2R_2^TR_1K_1^{-1}:=A\)被称为“Infinite Homography”,其物理意义有两种解释:
- 图像i中一像素\(p_i\)位置确定的光线,其灭点(vanishing point)在图像j下的投影矩阵:\(p_j=Ap_i\)
- 可以认为\(A\)矩阵就是光线方向在两个相机之间的变换矩阵
我们暂且拿公式\(\eqref{homo1}\)来玩一玩,看看它能推出一些什么有趣的理论。我们可以从理论上证明:
双目匹配中,经过rectification的两张图像,correspondence search只需要在水平方向上进行。
看起来... 好无聊的理论。不过我仍然要来试一下:首先假设双目的相机内参一致,也即\(K_1=K_2\),并且若是经过校准(外参也经过标定)的双目相机,应有:\(R_1=R_2\) 以及 \(C_1\)与\(C_2\)在相机z轴坐标上一致(其一的光心在另一相机的xy平面上),那么由公式\(\eqref{homo1}\),可以推出: \[ \begin{equation} z_2p_2=z_1(I)p_1+K_2R_2^T(C_1-C_2) \end{equation} \] 由于相机z轴坐标以及方向均一致,故对于同一个点,\(z_1=z_2\),而\(K_2R_2^T(C_1-C_2)\)只有x轴方向不为0,故可以知道: \[ \begin{equation} p_2=p_1+\alpha v_x,\text{ in which }v_x \text{ only has x component} \end{equation} \] 这也就说明了标定后的双目只需水平进行correspondence search。
2.3 对极约束与基础矩阵
2.2中实际上我们已经得到了一个重要的矩阵\(A\),用于进行灭点的映射。当然,这部分只是重要公式\(\eqref{homo1}\)的一部分,观察公式\(\eqref{homo1}\)的第二部分\(K_2R_2^T(C_1-C_2)\),不难发现,这部分是将世界坐标点\(P\)用\(C_1\)带入到公式\(\eqref{second}\)中,也即\(C_1\)在相机2下的投影。我们将这个投影点\(K_2R_2^T(C_1-C_2)\)称为极点(epipole)
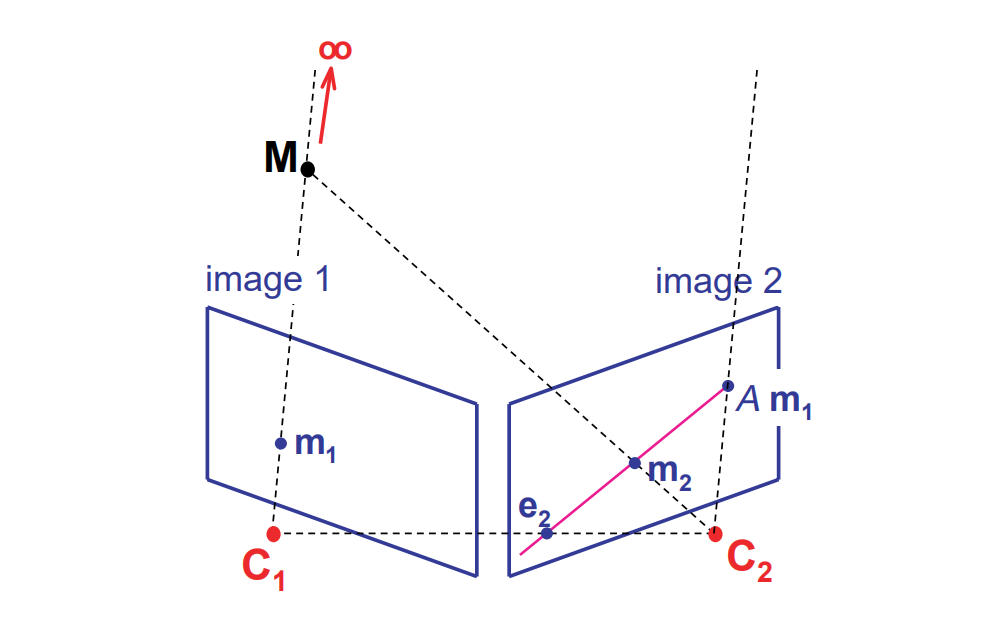
如图,\(e_2\)就是\(C_1\)对应相机的极点。而另一个点\(Am_1\)(灭点的映射)。而由于公式\(\eqref{homo1}\)对应了一个线性映射,并且有两个点已知:
一个结论
我们可以知道,投影在相机1下,并且像素位置为图上\(m_1\)位置的所有3D位置点,将会投影在相机2由\(e_2\)以及\(Am_1\)确定的直线上。
我们将这条线称为\(m_1\)在相机2下的极线(epipolar line)。
我们回过头来看2.2中的双目问题,由于未标定的相机(正如上图所示)是双目相机的一般化:
Suppose we have two images, taken at the same time and from different viewpoints. Such setting is referred to as stereo.
在一般的两相机 (stereo) 情形下,进行correspondence search应该是在极线上进行,而标定后的简化双目模型,其极线就是特殊的水平线。由于:
- 极点(如\(e_2\))根据定义,由于其在\(C_2\)所在的X轴上,投影不存在,可以认为在无穷远处
- 对于相机1的任意一个位置,其投影灭点投影应该是存在的,但与一个X轴上无穷远点形成连线,可以(intuitively)认为形成的极线是水平的。
这也反过来说明了双目问题水平搜索的正确性。
讨论完双目问题之后,再来细致地看一下“一个结论”中说的投影点必须在直线上这一结论。此时我们知道\(e_2\),\(m_2\),\(Am_1\)在同一直线上。这能导出什么有用的信息?显然,三者线性相关,列向量组成的\(3\times 3\)矩阵缺秩。 \[ |\begin{pmatrix} e_2 & Am_1 & m_2 \end{pmatrix}|=0, \text{ where |·| means determinant} \] 注意上述矩阵\((e_2 \quad Am_1\quad m_2)\)每一列的第三分量都是1,并不只是简单的一个二维矩阵。显然,\(e_2\)与\(Am_1\)确定的平面法线垂直于\(m_2\):
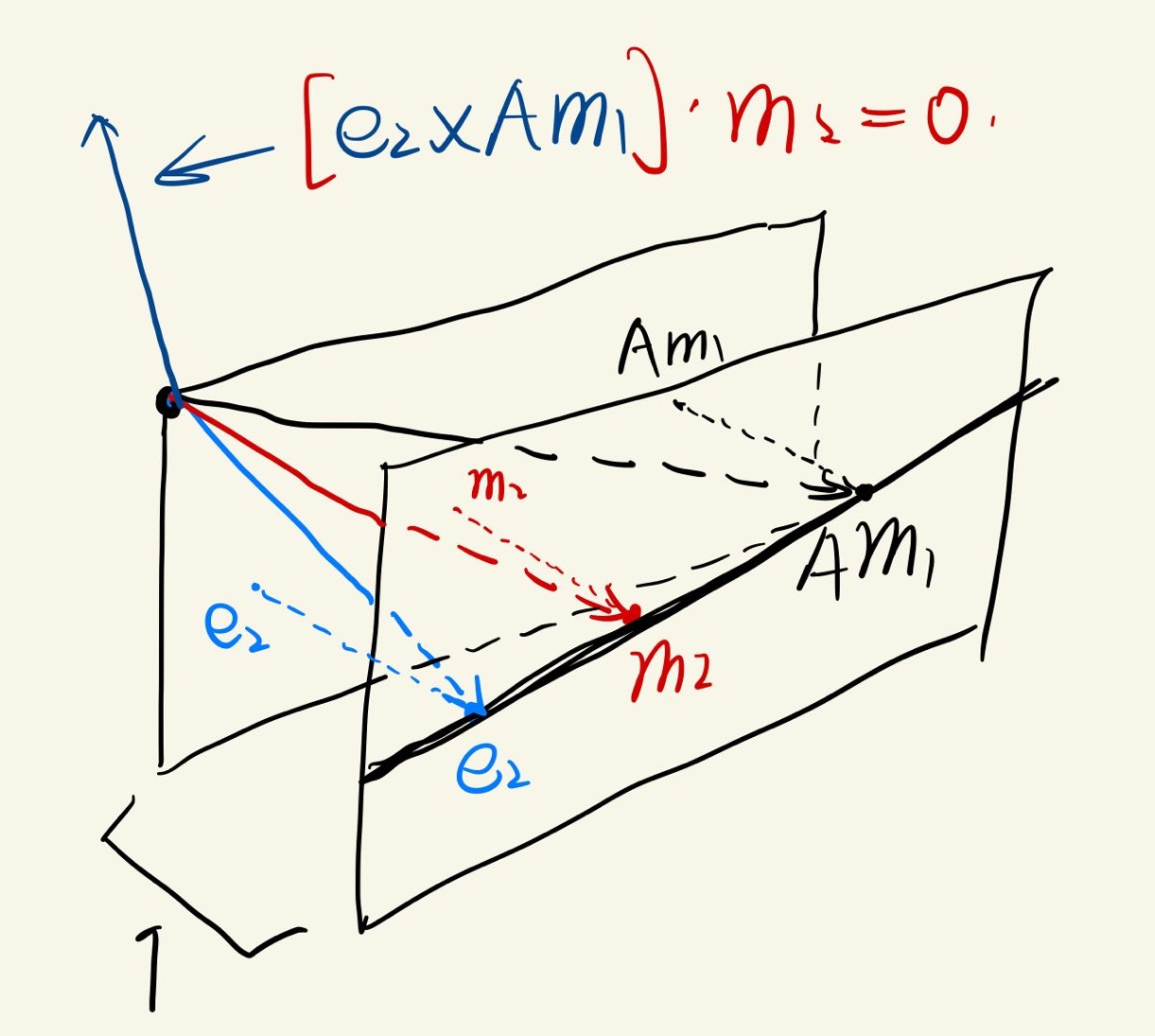
用goodnote随便涂了两笔,其中蓝色,红色以及黑色线才是真正的向量。由于外积可以写为反对称矩阵形式,也即: \[ \begin{equation} a\times b=[(a_1\quad a_2\quad a_3)^T]\times b=[a]_\times b=\begin{pmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{pmatrix}b \end{equation} \] 则可以得到: \[ \begin{equation} |\begin{pmatrix} e_2 & Am_1 & m_2 \end{pmatrix}|=0\iff m_2^T([e_2]_\times Am_1)=0\rightarrow m_2^T([e_2]_\times A)m_1=0 \end{equation} \] 我们把矩阵\([e_2]_{\times}A\)称为:基础矩阵(fundamental matrix)(\(F\)),其限定了由对极约束的两个图像点之间的关系。
III. ECCV 2020: Atlas
最终重建基于TSDF (truncated-SDF)。网络主要结构:
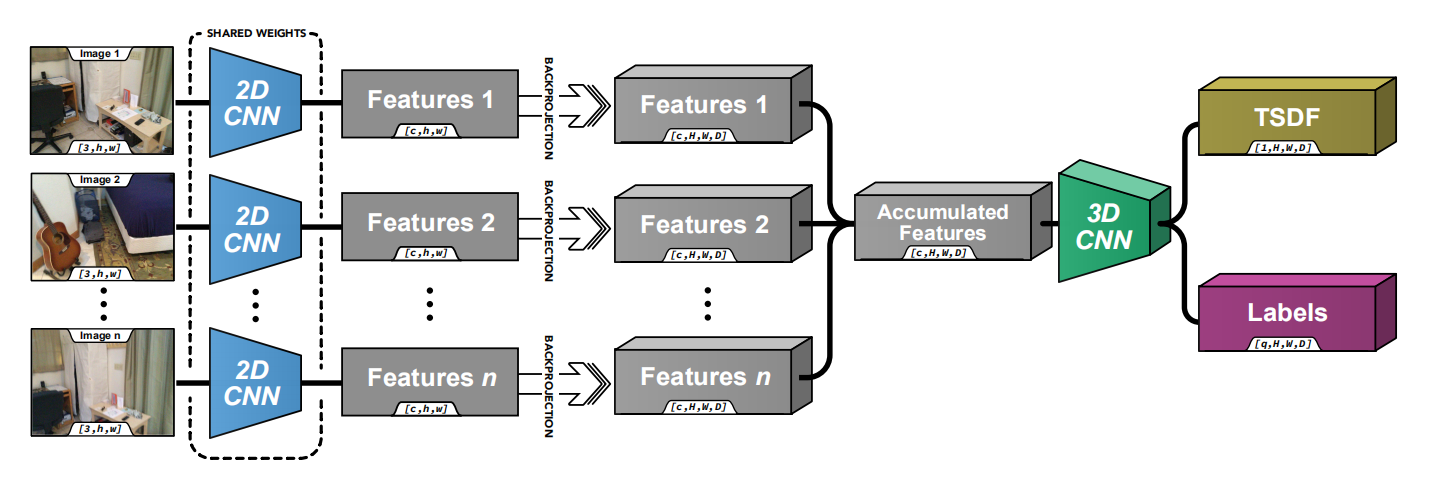
经过流程主要是:
- 2D特征提取,提取每张图像点的特征。
- 特征反投影,也就是由2D变为3D。这个反投影过程基于:
- 空间voxelize,作者称之为feature volume
- 相机模型,将一个点的特征投至与其关联光线穿过的所有voxel(如果我没理解错的话)
- 增量融合:一张一张图像叠在一起,形成的feature volume 变换到统一世界坐标系下 增量叠加。
- 形成一个dense的feature volume,这点我简单说一下:
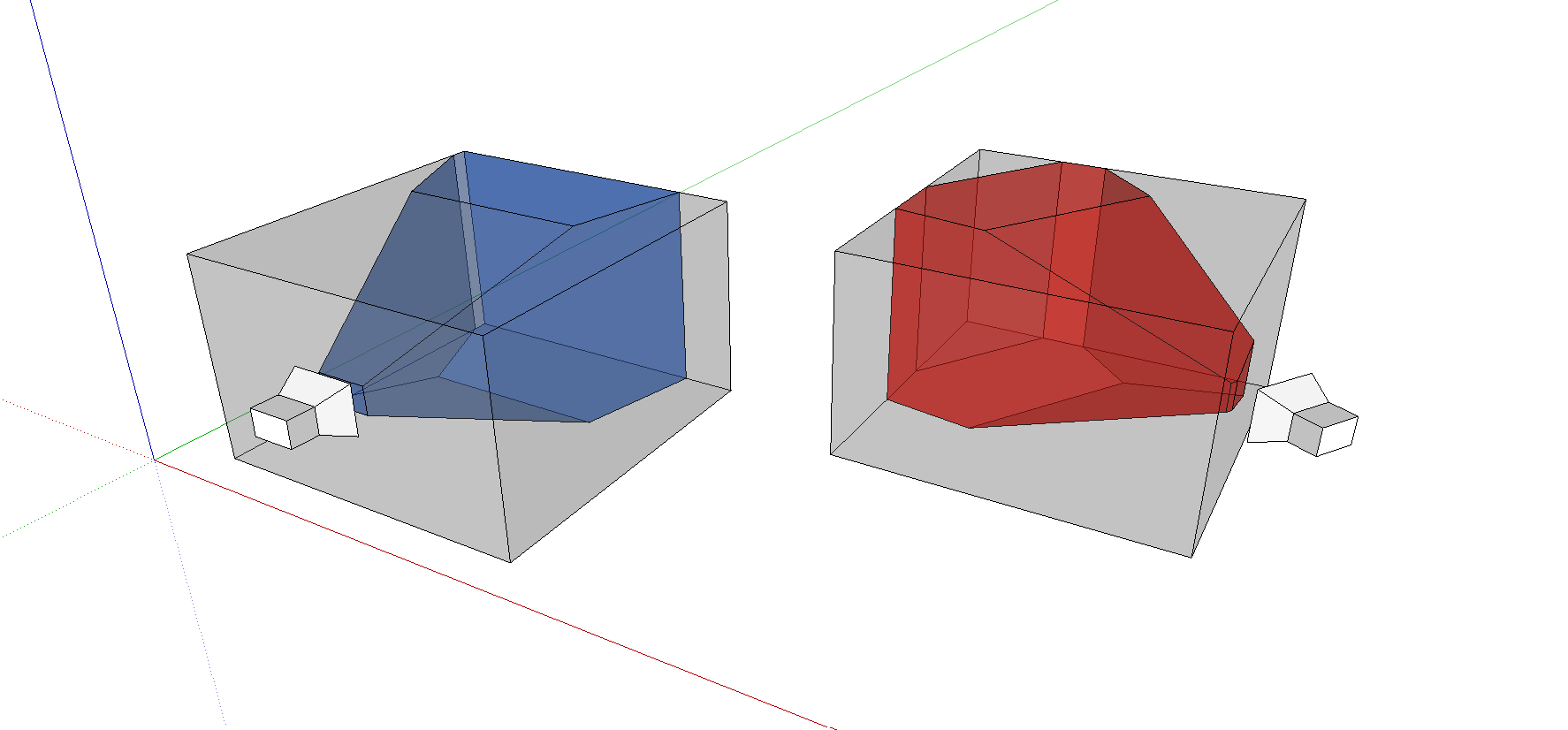
由于每张图像都会形成一个volume,比如蓝色的为相机于位置1全局volume中得到的反投影,红色为相机在位置2下于全局volume中得到的反投影,为了方便观察,我将两者分开(实际上全局只存在一个灰色的volome),两者叠加:
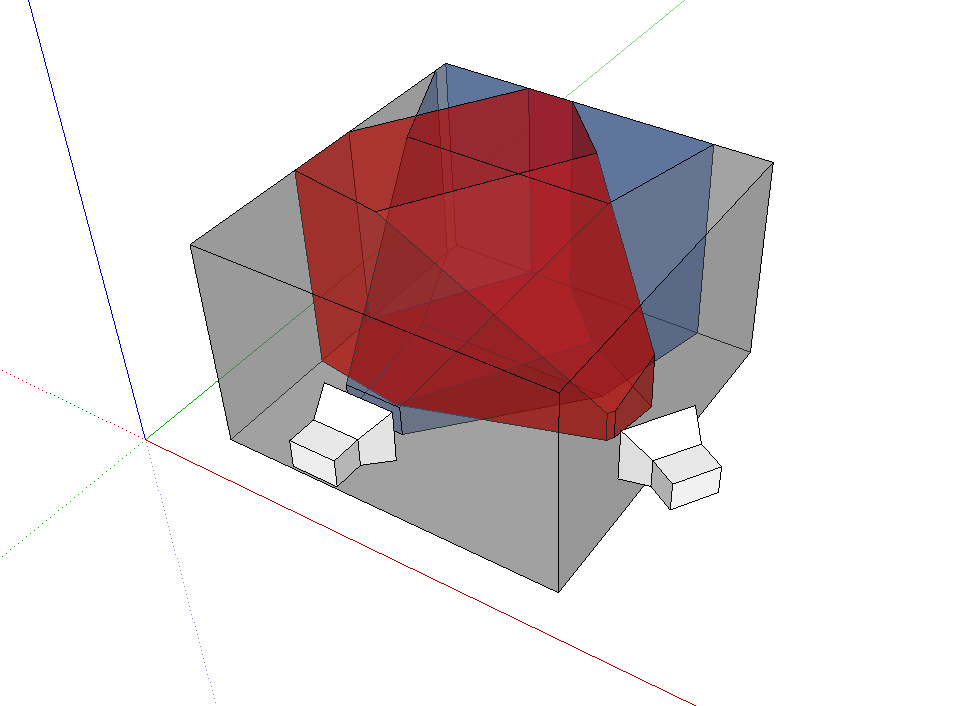
其中有些部分会有叠加,并且如果:某一部分在位姿1下观测到(在蓝色frustum内),并且也在位姿2下观测到(红色frustum内),由加权running average,特征会被保留,如果某些特征只在辆frustum的对称差集内(只有一个位姿有观测),那么加权平均将会弱化这些特征的存在性(毕竟如果在很多帧的情况下,某个位置都只被一个位姿观测到,那么大概率这个位置被遮挡了或者是一些不重要的角落)。根据加权平均(原文公式(3)(4)),观测点越少,特征越不显著(幅值越接近0)。
- 下一步是3D encoder-decoder模型,使用了\(3\times3\times3\)卷积以及\(1\times1\times
1\)卷积(用于特征维度的变换),关于3D卷积的一点点分析,见此PDF:[TODO]
- 形状还是类似bottleneck
- 作者在此处用了以下一些手段来保证训练的效果,因为这一部分直接回归TSDF(事关结果质量):
- encoder-decoder模型由于有bottleneck形状,上采样过程中每层都会输出TSDF,在不同精细度下与ground truth进行对比监督
- TSDF中的“Focal loss”,由于3D重建中存在大量empty space,对训练其实没有帮助,TSDF距离大于0.99者被强制设为1,并且阻断反向的梯度流动,这样这些voxel对结果将不产生影响
- 惩罚墙中墙等现象,由于重力存在,3D重建简单场景时,竖直方向是可以整体来看的,比如对于一座简单的山(没有空洞,没有大于等于90度的峭壁),一整个voxel volume中,对于平面上任意竖列voxel,一定是下部存在voxels(山),上部不存在(空气)。并且由于TSDF重建是用marching cubes寻找等势面,重建的voxels只存在于表面,内部应该也不会有。故在这种简单情形下,我们可以认为,每一列就仅应该存在一个点(表示简单山表面)。
- 上面的意思就是说:如果在这座假想的简单山内部进行采样,由于内部是不存在表面重建的voxel的(空的),我们的重建不应该在对应位置增加一个 墙中点。
However, to prevent the network from hallucinating artifacts behind walls, outside the room, we also mark all the voxels where their entire vertical column is equal to 1 and penalize in these areas too. The intuition for this is that if the entire vertical column was not observed it was probably not within the room.
不过笔者认为,关于“artifacts behind walls”这一部分,个人的解释还有一定问题(感觉有点强行解释),而网络上也无法找到对应的资料,如有人刚好读到此处并且有自己的理解,还望不吝赐教。
所以其中重要的部分是?个人认为是这么两部分:
- 2D特征反投影及加权平均融合:这一步真正生成了可用的feature volume
- 3D特征encoder-decoder:对于feature volume的重映射,并生成多尺度信息
其中feature volume生成有点意思,但个人认为可能这种正向的(2D->3D)资源消耗更大,毕竟每张图像都对应了一个feature volume(虽然是增量的叠加)。
IV. NIPS 2021: TransformerFusion
在上一小节末,我提到:正向的方法,其实我个人并没有看多少篇多视角3D重建的文章,也不知道是否有对应方法的分类。此文的特点就是:使用了反向的方法(3D->2D),并且使用了transformer(但个人感觉这里用transformer可能有些缺点,之后再说)。
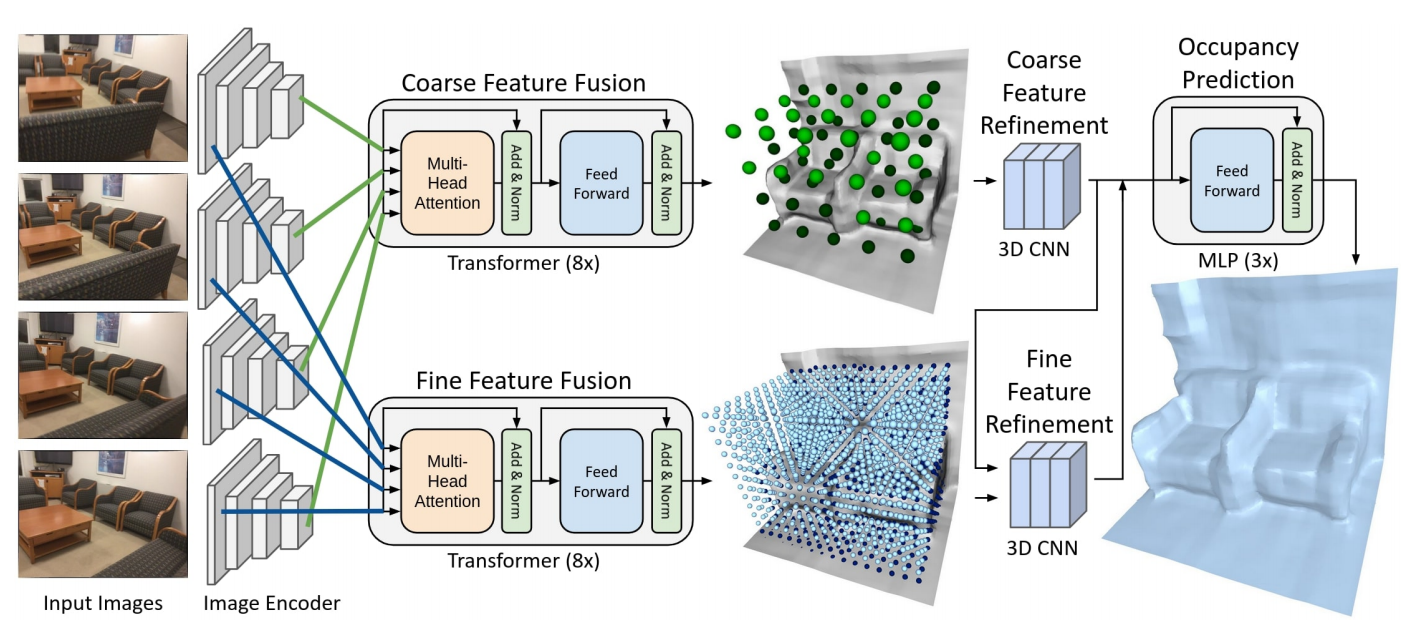
基于DL的方法开始总是离不开特征学习,至于怎么使用,这是不同的网络架构需要考虑的事情。
此文并没有使用层级,只是分成了coarse以及fine两部分,层与层之间在处理的较后部分才存在联系。其中要说的是transformer的 反向法。关于本文使用的tricks,个人不想再多说,什么free-space filtering(用类似于第三节说的“Focal loss”)以及refinement network,感觉大多数工作都会有。本节只想着重讨论此文方法与ECCV 2020方法的区别,以及其transformer的使用优劣之处。
与正向法相对,反向法对于每张图像上的特征并不直接反投影到全局的feature volume再进行求和(平均),反向法处理的视点是每一个3D voxel。在一个全局volume中,对于一个特定的voxel \(v\),我在不同的图像中查找:
- 此voxel在经过投影后,是否落在图像中?如果不再就跳过,如果在,将会选取本图像投影点附近的特征(根据线性插值)
正向法中是2D->3D信息流,使用反投影正向计算。而反向法是3D->2D的 查找 方式。从个人的感受上而言,笔者认为反向法更加优雅。
另一方面,transformer具体做了什么?对于任意一个重建voxel,不同图像拍摄得到的信息对此voxel的贡献肯定是不一样的,比如我要重建你的鼻子,那么距离近并且角度合适的图像学习的特征大概率比距离远或角度不合适图像产生的特征更加有价值。不同图像对某一点特征的贡献度 将由transformer来评定。
transformer不仅仅输出【经过attention机制评定贡献度】融合的多张图像特征,还输出softmax时的概率(也就是每张图像的贡献weight),这是为了进行 视角选择(view selection)。看到这里,我感觉到一阵莫名的亲切,这不就是2D SLAM里的点云融合吗?所以这也成了我认为本文存在的不足之处。
Transformer Pros & Cons
Transformer确实应该用,【贡献不同】这点从直觉上就很正确,与其使用别的方法进行学习,不如直接加attention,此处也非常适合attention操作。ECCV 2020一文中,对于不同视角下的特征,并没有明显的区分性,可以说是一视同仁,如果要说3D CNN进行了一些取舍,未免有些牵强。ECCV 2020中,如何区分significance,成了非常魔法的一部分。
Transformer是\(O(n^2)\)的,并且如果要深究,此处应该用Set Transformer这样置换不变的网络(并且人家Set Transformer至少还用induced point方法降低了复杂度)。而若要限制复杂度,就可以用 队列 的方式,我只需要保存不超过\(N\)张图片,算法就不会越跑越慢了。但这其实也不太爽,对于每一个voxel,我需要维护的是一个小顶堆。由于本网络输出每张图像的weight,根据weight选择,超出堆大小就drop堆顶weight最小的图像特征。这样的话,烦人的就是管理的复杂度了,相比之下attention复杂度可能还小些?如果考虑一整个feature volume,那么复杂度就是\(O(n^3N(C+1))\),其中n是volume大小,\(N\)是堆大小,\(C\)是特征维度,+1表示需要保存weight。
综上,transformer的attention,个人觉得是一个可保留的点,但是transformer带来的overhead个人感觉又是一个不可忽视的问题。至于怎么解决,个人粗略一想只想到 对于feature volume进行pruning(使得feature volume不要是dense的),毕竟3D表面重建,表面表面,重建的是3D空间中的2D流形,存储复杂度在理想情况下应该是\(O(n^2)\)的,那么多空区域扔一扔,都留下来的话,简直就是土匪,土匪都不如。
