2D激光SLAM中的SDF表征
SDF-SLAM
I. Intros
在家配电脑环境工程时,真没有事干,就只能看看论文了。之前太naive了,了解得少,只知道2D地图表征常用栅格图以及点云,不常用的是隐式函数(implicit function),却忘记了还有SDF这个中间表征。查找2D-SLAM文献时,蹦出了几篇SDF相关的文章,都还算中规中矩,通俗易懂(比起什么cartographer分支定界来说,简直太友好了,不过说起来,这几篇论文中除了cartographer魔改论文之外,真的谈了后端吗?):
Fossel, Joscha-David, Karl Tuyls, and Jürgen Sturm. "2D-SDF-SLAM: A signed distance function based SLAM frontend for laser scanners." 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2015.
Daun, Kevin, et al. "Large scale 2d laser slam using truncated signed distance functions." 2019 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR). IEEE, 2019.
Fu, Xingyin, et al. "Improved Signed Distance Function for 2D Real-time SLAM and Accurate Localization." arXiv preprint arXiv:2101.08018 (2021).
P.S. 本文内容并不多。虽然这有三篇论文,其中值得大篇幅讲的不可能塞在这篇博客中,不值得大篇幅讲的都在这了。
II. IROS 2015: 2D-SDF-SLAM
本文貌似先于cartographer发表,是2D SLAM中使用SDF作为地图表征的开山鼻祖。我们说,2D SLAM主要就是两种方法:
如果不知道我在说什么,参阅我之前的一篇英文博文【A Duality Problem of Representations】。这里的Eulerian方法指的就是使用一个静态的网格表征,比如基于(概率)栅格图的GMapping,Hector SLAM,Google's Cartographer。这种方式的好处就是:天然适合进行信息融合。
与Eulerian类别的方法互为对偶。你显式建模空间障碍物的分布,我就用一堆同时含有轨迹以及地图信息的粒子来代表整个空间。典型的方法就是粒子滤波。很有趣的是,要说用到PF方法的SLAM,GMapping也算是一个,所以GMapping实际上是:粒子表征含有Eulerian方法的Lagrangian方法。基于点云的方法,其实可以看作是这样的方法,因为其对地图的表征是动态的粒子。
SDF相比于以上方法,有这样一些特点:
- 相对于grid map,其需要的内存相对小一些。SDF,特别是截断SDF,只需要表征障碍物附近即可,而grid map很多时候都是全空间的。
- 相对于grid map,SDF最后到地图需要多一步 --- marching square(cubes)算法。虽然多了这一步,SDF以此求得的地图也是sub-grid(pixel)的。
- 相对于点云表征,SDF由于从某种意义上类似于grid map,其融合更加友好。
本文呢,主要贡献可以这么说:
- 提出了更好的SDF更新方法(这种更新方法与我熟知的方法大相径庭,个人认为此方法应该非常快速,但是存在一个大问题)
- 把SDF引到... 2D SLAM中来?当时来说确实可以算是radical的创新吧,但从现在的角度看来也不过如此?(嚯,垃圾hqy大放厥词)
本文的弊病(个人认为的):
实验也太简单了。
首先你仿真就仿真,把仿真的地图公开一下,别只公开一个啊 我们就用这个开源的Simple Two Dimensional Robot Simulator。我知道ROS已经集成了这玩意,但是这玩意怎么看都觉得有点简陋,万一你跑个巨简单的地图说,啊我这很好啊,这有什么意义呢?
真实的数据集也是自己采集的,而且环境很简单。没有公开数据集...
我说,至少也去radish上干一干GMapping啊,怎么只对比Hector SLAM
关于这篇文章的内容,我并不想多说,其SDF更新之术,我在第三节结合SSRR的论文一起说。而其配准方式,只是一个带Huber Loss的高斯牛顿法。等等,它好像也没有Huber核...。emmm,至于为什么我也不想深究这个配准后面的数学原理,是因为个人认为:
本质上,SDF方法的优化方法与GMapping的极大后验没有什么区别。GMapping中计算这个极大后验用了一个“似然域”,这个似然域是什么东西呢?你可以简单认为在每一个激光点处都有一个2D高斯核,叠在一起(有点像GMM)。这玩意就和SDF非常像了,只不过SDF是纯纯的距离,似然域像是个SDF的近似。那么既然方法上都没有太大区别,其实也就没有必要再理解一遍这个算法过程。况且我之前还自己设计过基于SDF的配准,只不过当时不知道我设计的东西有个术语叫SDF罢了。
III. 后两篇内容
3.1 SSRR 2019
本文是cartographer的魔改,作者自己说自己是基于cartographer,将cartographer只基于grid map拓展为了可以基于TSDF。本文我想说的不多,由于作者其实也没有介绍太多新的ideas,主要篇幅都是关于:
- 基于TSDF表征的表征更新:如何快速而有正确地计算TSDF(local SLAM,也就是前端的内容)
- 基于分支定界法的后端(带有回环约束的图优化)
说起来,TSDF的更新方法确实和我理解得非常不同。个人在2021年6月份简单研究了一下普通SDF的计算,当时写了一个具有普适性的SDF计算代码(也就是说,任意给我一段折线,我都能求出其SDF),关于我原来对SDF的想法,参见【远古SDF文档】。反正大概就是这个样子:
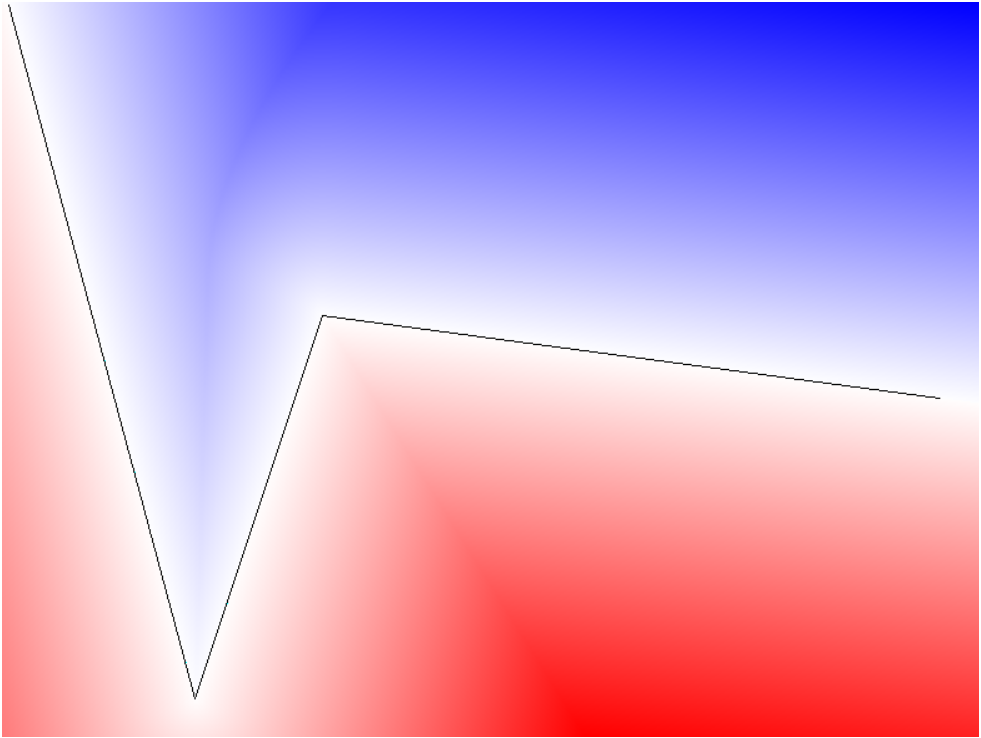
这样的SDF,计算当然是:对于空间每一点而言,计算其到折线段上距离的最小值(并且判定这个点在折线段的哪一边)。不考虑边的情况下,这样的想法计算量也还是挺大的,2D栅格上,每个点需要做【到不同线段的投影】,再进行一个最小值的reduce。所以个人从一开始就觉得,这种计算方法肯定比较消耗计算资源,不过这样的方法看起来是可以并行加速的(这里我想到了CUDA)。
但论文中提出了两种截然不同的方法:

这两种方法都避开了:一个点的SDF值需要与折线段上所有的线段发生相关计算的问题。虽然,所有线段都参与计算是最正确的方法(里面没有任何的近似)。但考虑到,激光数据进入是以点为单位的,如果转换为线段:
- 首先,转换为线段就存在不小的计算开销以及复杂度上相同的内存开销。不管是否进行抽稀(Douglas-Peuker算法)或者近似(拟合),都会至少是\(O(n)\)的计算量。并且,线段还不能直接用斜截式表示(存在奇异性)。
- 此外,转换为线段过后,如果没有做下采样操作,线段数目将非常多(虽然点云已经是一个sparse表征了),通常来说都会在100段以上。假如设grid纵横为n,线段条数为\(N\),计算资源消耗的复杂度将会是\(O(n^2N)\)
作者提出的第一种方法,称为projective ray方法,这种方法其实还是近似于grid map的思想。我用激光器光束模型来update每一个击中点附近的SDF值,简单考虑,我就认为在每一个击中点所在激光线上,我可以把激光线上点相对于击中点的距离直接当作SDF值。由于在这里,更新的每一个点都在激光线上,所以如果\(\text{range} + \Delta d\)是某个grid的深度,那么\(\Delta d\)就是SDF值,计算就非常简单了。但这种方法的问题也很大:
- 求出的不是真正的SDF距离,大多数情况下都不是“到最近表面的距离”,只有在激光束垂直入射表面并且附近没有其他表面时,这种方法计算的SDF才是正确的
- 在入射角度大,或者grid分辨率很低时,SDF质量非常差。在IROS 2015 SDF文中说到:
Cells which are both positive and negative are in conflflict as they are updated with both positive and negative distances, which do not tend to cancel each other.
借用IROS 2015中的图,表示一下大概就是下图这样。个人认为,这种想法简直就是在用【方法的前途】换速度。
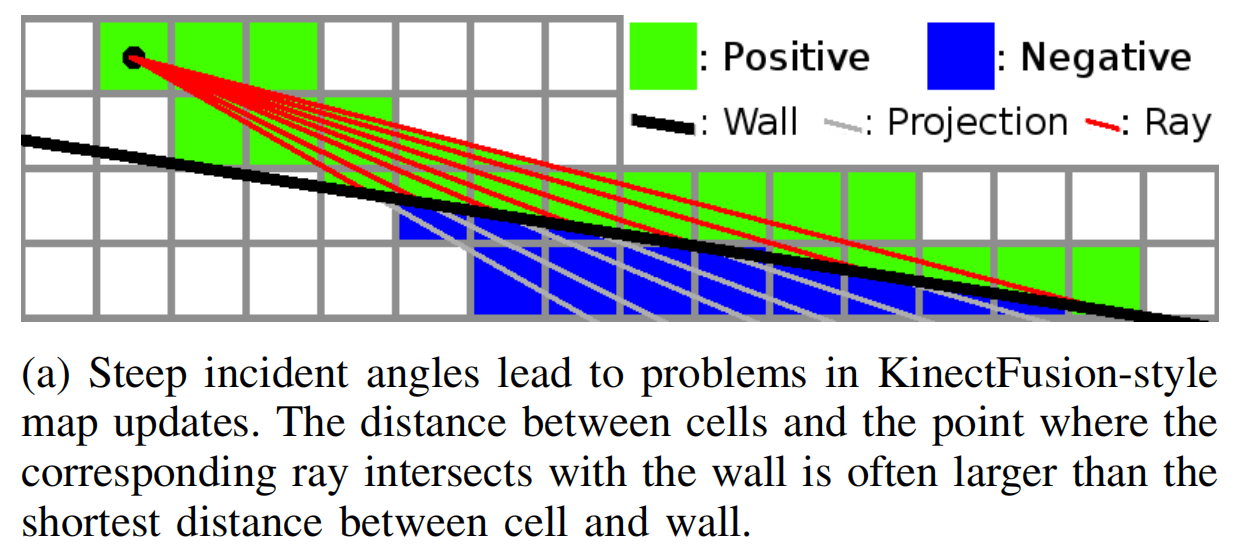
而作者提出的第二种方法,看起来更加正确。在这种方法下:
- 首先我需要evaluate每一个激光击中点的local normal(局部法向),这一步也不是那么好做,我在自研算法里有这个操作,需要进行初级分割,以免深度不连续位置导致法向量evaluate有误
- 根据局部法向,沿着局部法向的方向向内外扩展SDF,如图二(b)以及下图所示:
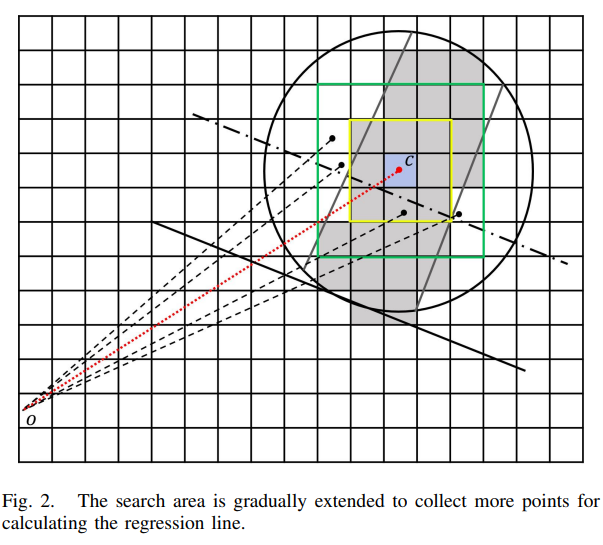
但个人觉得这种方法还是不甚优雅,在点特别稀疏的场景下,这样计算应该是会导致SDF稀疏的。毕竟你只update法线方向周围的部分点,如果点过于稀疏(1. 角度分辨率过小或2. 入射角度太大),那在垂直法向的方向上无法得到足够的coverage,就会出问题。
这里,分支定界法我不多说,因为我并没有深入理解到其方法的精髓。在这里不得不承认,运筹学虽然学习了分支定界法,但是太流于表面,可能当时会做题(意思是现在题都做不出来了),但并没有体会到这个思想的美妙性,关于基于BB方法的后端优化,个人可能会用专门的一篇博客来讨论(有关分支定界法本身以及其在SLAM中的应用)。
3.2 arXiv Preprint 2021
这篇文章,可能之所以是preprint,就是因为没有太多可以投的点吧,除了SDF更新之外,我只简单提一些本文提出的好的思想:
3.2.1 Free Space Update
是 空域的思想吗?有点这个味道,但是并不完全。作者已经想到了,可以利用与空域的冲突性,来剔除动态障碍物,只需要在地图中建立空域概念,如果一个hit观测出现在空域中(在多数帧下显示为un-occupied,本帧发现存在障碍物),那么大概率会是动态障碍物。这个思想在我们算法里也有,并且它的free space计算方法就和我们很像:
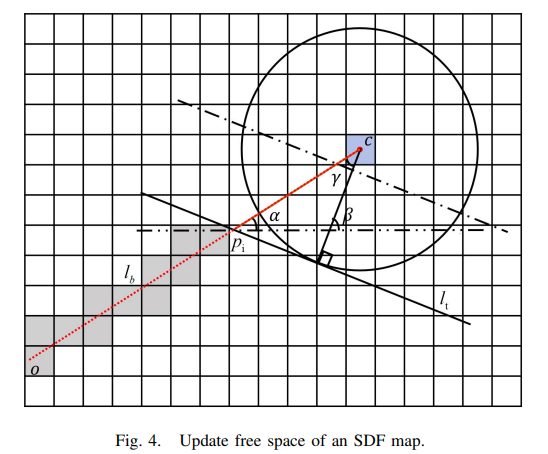
3.2.2 Expansion
作者也意识到纯法向SDF更新的问题(稀疏性),所以作者用了一个“迭代取点”的方法。首先,Deming regression至少需要三个点才能生成一条直线,在入射角度过大或者距离过远的地方,一个grid内部可能找不到那么多点,作者根据hit点的邻域关系逐步expand搜索域。举个简单的例子:
- 在某一个激光点的8-邻域内(扩展一次),只有一个点,显然两个点没办法形成regression,需要继续扩展
- 在8-邻域点对应的8-邻域内(扩展两次),找到了第三个点,那么用这三个点regress一条线并进行法向更新
- 垂直法向上的更新半径,根据扩展的次数确定,越稀疏的位置,扩展次数越多,更新半径就越大。
- 这样一种方法,应该至少可以消除大部分稀疏性问题带来的影响。
3.2.3 类似view selection
作者在 Improve Priority Strategy 一段中写到:
The cells closer to the cell that gives rise to the update are put on a higher priority.
SDF的标准定义就应该是:离谁近就用到谁的距离来更新。而不管是projective ray还是局部法向法,都不是按照“谁最近就用谁更新”的原则计算SDF的,那么就需要引入取舍标准:不同点计算的结果不同时,我取谁。作者这里并没有一刀切,而是用加权的方式融合。
3.2.4 Outlier removal
emmm,简单来说就是,剔除深度不连续点。这,叔叔我啊,可早就写过了。
3.2.5 子地图融合
这没有什么指的说的,对于这种显式或者隐式用了grid的方法,融合就是比较简单。