Neural Radiance Field【1】

Posted on Edited on In Views: Symbols count in article: 7.8k Reading time ≈ 7 mins.

Neural RF

I. Intros

​ 深度学习的大环境下，视图合成（view synthesis）必然不会缺席（毕竟没什么数学能力也能搞，是吧）。NeRF作为其中比较杰出的工作之一，文章后续也受到很多关注，包括但不限于【NeRF++，NeRF--，Point NeRF】。本文是一篇关于NeRF及其++版本的论文理解，后续将在[Neural Radiance Field【2】]中介绍Point NeRF以及NeRF的复现：

Figure 1. 拿个视频当NeRF demo是吧?（误）

II. NeRF本篇

2.1 文章脉络

​ 本文由于是神经网络radiance field表征的开山之作，所用方法以及思想都较为简单，清晰易懂。

​ 本论文有三个主要贡献：

  • 第一次使用神经网络（MLP）对连续的volumetric空间进行建模，并使用可微投影模型的离散近似设计优化方法
  • 设计了一种positional encoding，可以将低频的空间位姿输入转化为高维向量，提升模型的表示能力
  • 设计了一种层级化的采样算法，通过coarse-to-fine，coarse sampler采样结果对fine sampler进行指导，使得fine sampler可以更加聚焦于物体表面附近的采样，提升采样训练效率
Figure 2. NeRF网络信息处理过程

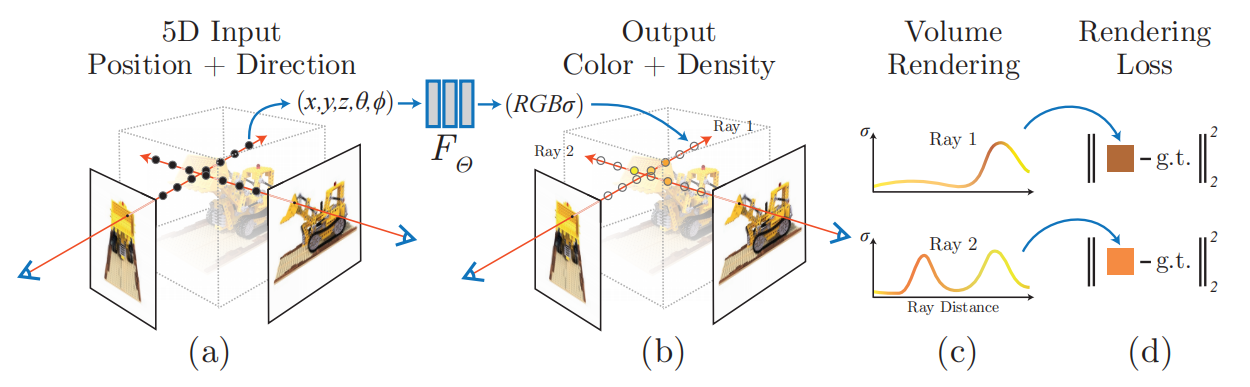
​ 网络的信息处理流程：

给定多张已知内外参的图像，从这些图像中，随机挑选一些光线（运用到了相机模型），在光线上进行点的采样（这里忽略coarse2fine层级化采样），那么这些采样点就会有平移旋转信息，分别被表示为（平移）\(\pmb{x}\)，旋转被表示成\(\pmb{d}\)（一个3D单位向量)

  • 采样的进行：为了避免使用固定的voxel volume（意思是说，作者不希望在进行voxel化之后，每次光线在volume中采样，打击到同一个voxel时得到的是一个固定的位置，这样网络最后的输出会直接与voxel的量化精度有关），作者均分光线为N段（采样N个点），每段内由均匀分布采样一个点
  • 但是显然，这样会采样到大量的遮挡点或者空域点，作者认为这非常不合适。故作者使用一个coarse sampler，一个fine sampler。coarse sampler采样更少的点（每条线段的等分N更小），这些点先在MLP中进行evaluation，判定每条线上哪些点属于比较好的点（接近实际的表面），fine sampler可以着重在这些区域进行采样
  • coarse sampler 采样得到的点也会参与优化，当然由于coarse sampler采样的点属于指导性的点，其evaluation不能存在太大的computation overhead，故作者同时也用了一个coarse网络，此网络也参与优化，优化可以使得此网络能更好判定采样区域的好坏，给出的权重更合理。此思想很有趣。

点进行positional embed之后，输入到MLP网络中，网络输出每个点：

  • 与位置以及方向（相机发出的光线朝向）相关的RGB值（相当于观测到的颜色）
  • 只与位置相关的opacity：可以认为，这是网络对于此点接近有效表面点的概率表示，或者单纯认为，这是空间中某点的光导率

最后颜色使用volume rendering模型进行渲染，可以得到最后的结果

2.2 一些问题

（1）论文理解过程中最初的阻碍是：radiance field究竟是一个什么概念？

We represent a static scene as a continuous 5D function that outputs the radiance emitted in each direction (θ, φ) at each point (x, y, z) in space, and a density at each point which acts like a differential opacity controlling how much radiance is accumulated by a ray passing through (x, y, z)

​ 其中 (θ, φ) 应当是自变量， (x, y, z) 也是自变量。给定一个观测角度，以及一个点，输出rgb以及一个类似alpha通道的东西。个人的疑问在于，此点（x，y，z）到底是什么？与RGB之间的关系是什么？首先，上文所说的radiance，指的完全就是RGB值（光线），对于一个固定点而言，不同方向观测的颜色可能是不一样的（由于光照的区别），故RGB值不同，但只有一个RGB是无法完成视觉建模的，需要透明度。比如，对于物体正前方的一个空气点，在与观测物体相同的方向上，我确实也可以认为此点发出了与物体相同颜色的光，但在别的视角下，物体与此点在成像平面上并不重合时，空气点产生的RGB就需要被透明度加权成0，使之不影响最后的RGB输出。

​ 但说实在的：“a differential opacity controlling how much radiance is accumulated by a ray passing through (x, y, z)”，我对这句话的理解并不是特别深。在我粗浅的理解中，此句的意义是：opacity量控制的是最后渲染的结果，本点在成像时能对结果产生多大影响？渲染到2D成像平面上某一(u, v)点的颜色，是不同3D点产生光线颜色在此处投影的加权平均。

​ 在后文所提到的NeRF++一文中，作者通俗地解释了NeRF训练的结果。

（2）训练过程中同一条光束上，不同的3D volume点最后融合成的结果是否与之前看的某几篇multi-view depth estimation方法相同？

​ 并不一样，multi-view depth estimation 人家真的使用了dense voxel volume，但本工作中，query点仅限于光束上，并不会实际变换到某一个voxel volume中，再进行叠加。本文训练query得到的点，并不在固定的voxel中，作者也提到，固定的voxel会使得最终的结果与voxel分辨率相关，并且作者最后得到的结果，是一个有能力映射连续空间的函数。

（3）从直觉上讨论，positional embeddings为什么有助于表征高维信息？

​ 此处的positional embeddings不是learnable positional embeddings，并且也不是简单暴力地从\((x, y, z, \theta, \phi)\)通过某一个神经网络（比如一个MLP）映射到高维空间，因为简单这样做没有任何意义，毕竟之后的场景表示就是一个MLP，MLP接MLP相当于一个更大的MLP。作者在此处用了类似于Transformer的处理方法，也即用了一系列不同频率的 \(\sin\), \(\cos\) 函数组合成一个高维表征。那么如何映射到一个高维向量我们已经清楚了，重点是：为什么？

​ 第一，如果从个人直观上理解来看，之前我们讨论分类器时，经常会说：低维分不开的，某个高维空间下可能就可以分开了。低维空间下的物理临近性，在高维空间中不一定成立，也就是说，低维距离近的数据可能在高维的差异很大。两个相近的5D输入，由于深度不连续或者物体形状突变，观测到的颜色可能截然不同，那么这种输入上的空间上趋于连续平滑性质，便是低频，经过非线性映射之后，自然是可能到某一个高维空间的，在此高维空间下，两个原近似5D输入有较大差别，也就形成了高频信号（低频即平滑缓变，高频则间断跳变）。

​ 第二，作者提供了一篇ICML 2018论文[1]，论文中提出：

By using tools from Fourier analysis, we highlight a learning bias of deep networks towards low frequency functions.

​ 如果不预先将本身就是低频信息的位置与旋转变换到高维空间下，神经网络的表示能力将会受到更大的削弱（低频输入--> 网络倾向于学习低频信息 --> 欠拟合）。

（4）volume density是视角不变的，有什么道理吗？

We encourage the representation to be multiview consistent by restricting the network to predict the volume density σ as a function of only the location x

​ 如果说density只与位置有关，那么作者相当于潜在地做了物体表面预测（预测哪些是实际的物体点，哪些是空气点或者是内部点），当然，也可能纯粹是表面估计+透明物体透明度估计。NeRF++中也给了一个类似的、非常简明的观点。

（5）以下公式中为什么有一个指数分布？是之前的一个已有模型吗？ \[ \begin{equation} C(\mathbf{r})=\int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))c(\mathbf{r}(t), \mathbf{d})dt, \text{ where } T(t)=\exp\left(-\int_{t_n}^t\sigma(\mathbf{r}(s))ds\right) \end{equation} \] ​ 是的，这涉及到一些图形学邻域的知识。Beer' s Law中提到的Volumetric Attenuation[2], 如果认为某个半透明材质的透明度（光导率）是恒定的，穿过其中的光线出射时的光强与在其中穿行的距离成负指数关系。此指数的存在与 光线穿过一个具有一定导光率（可以认为是空间中有一定density阻挡光的粒子）的介质而不与这些粒子碰撞的概率。由于作者是在光束上离散采样，最后作者用了一个离散求和近似了此积分，甚至最后作者还说：

This function for calculating \(\hat{C}(r)\) from the set of (\(c_i, \sigma_i\)) values is trivially differentiable and reduces to traditional alpha compositing with alpha values \(\alpha_i=1-\exp(-\sigma_i\delta_i)\).

2.3 一些扩展想法

  • 个人感觉这个模型是可以预训练的？通过仿真，可以生成很多视点位姿差距很小的图像，即使是简单的场景，使用这种方式是否可以创造一个“具有空间连续性”并且“具有一定2D场景还原能力”的大环境？使用仿真数据，生成小视点位姿差距图像训练，并进行监督（而非投影回到输入图像），可能可以帮助连续平滑函数的构建？
  • 已知NeRF是 volumetric-based（弱volumetric），那么Point-based NeRF的地位是否有类似于 Eulerian <---> Lagrangian对偶的关系？换言之，Point-based NeRF在NeRF问题上相较于volumetric-based NeRF取得的成功，是否在激光SLAM领域也有指导意义？

III. NeRF++

​ NeRF++可以说是一篇很好的NeRF补充文，其中不光讨论了NeRF的成功原因，并且也提出解决了NeRF在无约束场景（存在大范围背景）下效果不好问题的方法。个人的建议是，如果看了NeRF一文，想要加深理解，一定要看看NeRF++。

​ 本文的主要贡献有两个：

  • 解释了为什么NeRF可以在有“shape-radiance ambiguity”问题的情况下，仍然得到很好的结果
  • 提出了一种新的parameterization方法，用于解决unbounded大范围背景场景问题

3.1 Shape-Radiance Ambiguity

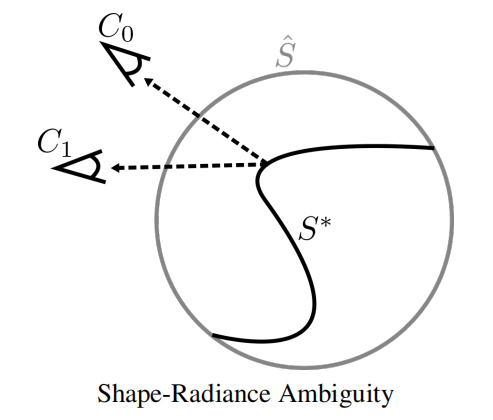
Figure 3. Shape-Radiance Ambiguity 问题：形状不对但是颜色对了也能恢复少部分视角下的图像

​ 乍一看，看不懂。这啥意思？我们首先来看NeRF的输出，NeRF对于每一个3D点，在每一个视角下，输出opacity（view-independent）以及RGB（view-dependent）。此opacity，正如作者所说：

NeRF reconstructs an opacity field σ representing a soft shape, along with a radiance field c representing view-dependent surface texture.

​ 就是物体形状的一种soft（指模拟量，在物体真正形状附近的值是平滑过渡的）表示。那么在仅仅渲染好一个（或者少数的train set）视角的情况下，RGB与opacity会如何被训练？本文作者举了一个这样的例子：假设我训练时仅有少数几个视角，我认为地将物体的形状（opacity）训练成一个球，而颜色，则根据重投影（渲染）的结果与原图的差别进行优化。那么可以对比一下，预期结果与这样训练的结果之间的差别：

​ 最后的结果，应当是：某一3D点在某一视角下观测在成像平面上体现的颜色 = 不同点 部分准确的 RGB与 准确的 opacity（对应了准确的物体形状）的加权和。

​ 此结果则是：某一3D点在某一视角下观测在成像平面上体现的颜色 = 准确的RGB * 1（opacity在单位球上）。

​ 作者想表达的也就是：在不需要精确model 3D形状时，在某几个少数视角下，我也能把正确的2D图像输出。比如下面这张街头艺术，显然作者并没有在墙上真的搞一个这样的洞，但是他却能成功在这个视角下，把他想要的3D效果给画出来。

Figure 4. 2D-3D视觉错觉：形状完全不对，但是能表示正确的3D意义

​ 这是个什么问题呢？显然，过拟合问题。少数视角下，我只需要通过硬调输出使得与输入一致，完全不用管原物体形状胡来，就能达到一个低loss，这样的结果有泛化能力吗？显然是没有的。NeRF++作者做了一个关于【球形opacity】物体的实验：

Figure 3. 换视角后的泛化能力极差

​ 那么为什么NeRF避免了这个问题呢？作者认为：如果不尽可能准确表示物体的3D信息（opacity尽可能正确），那么RGB输出对应的函数将会是高频的，不平滑的函数。很显然，一个球状物体，如果要在几个不同的观测下看到的都是一张，如上图所示，挖掘机的图案，那对于每一个3D点，它在不同的观测角度下的颜色 必然是差别巨大的，小的观测角差别就能带来很大的输出变化，这个函数显然是高频的。

​ 而由论文[1]，我们已经知道 神经网络学习高频函数相对困难，低频函数会被优先学习。而低频对应着平滑，关于这点，作者说：

For the correct shape, the surface light field will generally be much smoother (in fact, constant for Lambertian materials).

​ 确实如此，正常物体，尤其是大多数人造物，颜色都是分块相等的，不同视角下由于光照问题可能有一定差别，但总体上说，应该还是具有平滑性的。此外，高频函数如果需要被神经网络所表达，将需要更多参数。毕竟对于MLP来说，有限的参数，代表了对空间有限的线性划分，而有限的层数（对应有限的activation），则对应着有限的复杂形状（非线性变换意味着网络可以表达更加形状丰富的流形）。而且，根据经验，过拟合（高频函数）都是在over-parameterization以及样本过少时发生的。

​ 在此基础上，作者还认为NeRF的网络结构设计也与 shape radiance ambiguity 的消除有关。但这个理论就不如上面所说想法那么有【Ah-hah】的感觉了，在这里我就不赘述了。

3.2 Inverse Sphere Parameterization

​ 用一句话来总结这部分工作，就是：Inverse depth。在双目视觉中，假如我们要直接表示深度图，通常是做不到的，尤其在室外。假设我们看到了天空，那么天空的距离是多少呢？我们debug查看一下变量，奥 NaN 啊，那没事了。对于场景中存在较多较远物体时，即使没有inf距离，也可能使得网络不得不学习【输出需要加一个大bias】这种傻特征。在双目等应用中，通常我们都取inverse depth，距离远就0，距离再怎么近也不可能1/0。

​ 看NeRF一文中的demo就知道，它的输入，都是一些限定大小的物体，并且这些物体还特地去除了背景。emmm，你说如果一个网络只能处理这种数据，我们会评价它：未来可期。那么本着【未来工作未来录】的想法，是我做审稿人我就给你拒了（误）。个人认为，至少背景还是要有的吧，不然看起来还真缺点实际意义。NeRF++作者认为，常规NeRF，由于训练使用的是点采样这种方法，对于大型unbounded场景来说，远距离下采样要多少个点才算够？离散的话，能很好近似渲染过程的积分吗？太稠密的话，是否会使得网络专注于背景建模，使得前景的效果变差？并且也消耗计算资源？作者发现确实会这样：

Figure 5. 经典鱼和熊掌不可兼得

​ 针对此问题，作者提出了这样的方法：

  • 由于多视角重建问题，一般都是针对物体的（有focus，有一个可以 被bound 的对象），那么此对象周围部分bounded区域，用一个NeRF来描述，此NeRF什么也不需要改，因为处理的区域是小范围bounded的区域。选择一个球型区域，所有的相机位置都被包括在这个球型区域内。
  • 外部区域，全部用inverse sphere表示。
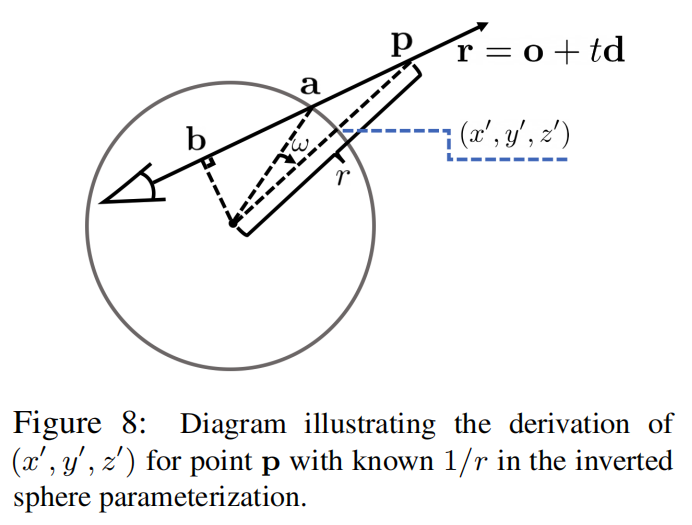
Figure 6. 已知光线方向与r求其在inverse sphere上的投影

​ 上图就能很清晰地说明inverse sphere的工作原理。对于一个已知r，当r小于一个阈值\(r_0\)时，说明此点在bounded区域内，可以直接用NeRF及其对应的采样求和近似积分来计算渲染结果。大于\(r_0\)时，用inverse sphere对应的采样方法：只需要在\(r'=1/r\)， \(r'\)在[0, 1]区间内随机采样即可。由于3D点点p在光线上（不在sphere半径方向上），一般需要根据r值以及光线方向，求其在inverse sphere上的投影位置\((x',y',z')\)，这里就不赘述方法了。

Reference

[1] Rahaman, Nasim, et al. "On the spectral bias of neural networks." International Conference on Machine Learning. PMLR, 2019. 【注：作者貌似ICML转刊PMLR了】

[2] Philipp Slusallek, Computer Graphics: Chapter - Volume Rendering.