NeRF论文复现
NeRF
最近工程浓度太高,关于【如何设计】以及【为什么】的思考显著少于【如何实现】以及【怎么解决】。为了平衡科研与工程,我复现了最近读的一篇多视角重建论文(见上一篇博客 Neural Randiance Field【1】):
NeRF这篇论文,读的时候觉得作者写得还是非常清晰,只要搞清楚了基本概念,流畅地读下来基本上没什么问题。但实现过程中,发现到处都是坑(坑主要来源于个人没有清晰的设计思路,不同模块间的输入输出连续性不强,导致接口经常改动,此外... 有些问题确实也挺坑的)。有别于NeRF的官方tensorflow实现,本论文复现使用Pytorch + CUDA,主要代码中约有50% CUDA,50%python。本论文主要记录复现思路,以及复现过程中遇到的主要问题。复现见Github repo: Enigmatisms/NeRF

II. 困难部分
2.1 CUDA加速的随机采样
个人觉得,NeRF中有很多操作都可以用CUDA实现,正好我很长时间没有写过CUDA程序了,想借此机会回忆一下CUDA编程以及调试。首先我从随机采样下手。NeRF的直接随机采样主要用在coarse network中,由于我们的(以及作者的)设备capacity不支持对100张(800×800)图片的直接采样(GPU global memory根本不够),而我们同时又希望在训练过程中,渐进地覆盖训练集的所有像素,故需要随机采样。
复现过程中,算法逻辑并非困难的部分。比较绕的地方在于输入输出的设计。采样需要输出什么?我只需要点以及对应的RGB信息就可以了吗?是否还需要其他的辅助信息(诸如,点属于的位姿id等等)?采样的修改,迭代了三个版本:
初代版本的输出shape是:(采样光束数量,每条光束采样点数量 +
1,3)。至于为什么要+1,在每条光束的最后一个输出数据,是产生此光束的图像RGB信息。而之前的输出数据则是按由近到远的采样点。本版本实现已经输出一个shape为(采样光束数量,每条光束采样点数量)的lengths
tensor了,用于渲染,使得渲染时不需要再根据采样点3D坐标反算一遍每个点到相邻点的距离,lengths
张量已经计算好了。但本版本缺少重要的信息:光线方向信息,光线方向信息需要用在逆变换采样以及coarse
samples & fine
samples的合并中。虽然也可以通过后期点差值来计算,但这毕竟也不是一种很高效的方法。此外,本版本的一个
重大缺陷
就是,在写采样之前我完全不知道数据集是什么样的。我直接写了一个根据内外参数采样的算法,但是数据集中
相机内参只有focal(并且以FoV的形式给出),没有各轴的放大系数,内参是不完整的。故我被迫又去学了一下如何只用焦距计算相机坐标系下的点,并放弃了本版本代码。
第二代算法实际上已经功能完备了,输出的shape是(采样光束数量,每条光束采样点数量 + 1,9),在每条光线的最后一个9维位置,保存了(对应相机的平移,光束的方向),9维个维度在其他数据中的意义分别是:
- 前三维度:采样点(x, y, z)
- 中间三维度:光束方向(未归一化)
- 后三维度:RGB值(方便比较)
第二代版本最后的结果始终是错误的,并且刚开始的时候,我还没有掌握这种网络debug的精髓。最后一想,既然是多视角重建,结果有误,我干脆就一直输入一个视角下的图片,看看输出是什么。结果发现它给我输出了一个烧杯(lego训练集第一个)。开始我怀疑是获取采样点这一部分实现有误,我甚至把官方实现的get_rays函数抠出来,相同输入对比输出之后发现完全一致...
个人最后进行了一些代码的简化,但我并不认为是代码简化导致了训练的成功,反倒是positional
encoding的实现让人感觉很迷。摘取官方pe生成函数对比实验时,我发现官方的pe比我的维度大,前面多了三项,其余项均相等。这是因为官方把原输入给cat到positional
encoding之中了... 但你论文里没写你这么干了啊nmd,一遍说是 positional
encoding
可以使得原始输入没有低频偏移,一边cat了低频信号也不写上?总之,做了这个改动之后,网络成功了。当然,在成功之前,为了避免所有可能的错误,我把所有用CUDA实现了一遍的函数功能又用Python实现了一遍。
2.2 CUDA加速的逆变换采样
如果可以彻底抛弃此结构,NeRF的训练至少可以加速25%。但是,如果没有这个结构,vanilla NeRF这个暴力采样的网络很可能会有很大的质量损失。此结构的主要思想是:
用两个网络,一个称之为粗网络,记作\(N_c\),另一个称之为精网络\(N_f\),粗网络对精网络有指导作用,指导精网络采样。 --- 为了好看,引用自我自己
我们以论文中的参数设置来看。粗网络对于每一条光线,都会先在near bound 以及 far bound之间,划分64个均匀间隔的段。为了使得最终的结果不受到固定分段的影响,在每个段内采样时,不直接使用段的中点,而是在段内随机采样。这很可能类似于一种叫做【序列超分辨率重建】方法中所用的思想:
- 拍摄一个场景,一张图片的精度有限,但假如拍照时相机在轻微抖动,抖动过程中拍摄到一系列图片,这些图片可能刚好在信息上具有互补能力。详见【知乎,diao图重建】
从这个思想的角度出发,我们可以认为,随机采样的过程就可以有效将整条光线覆盖,这样,精度就不会受到分段间隔的限制。好,回到\(N_c\)的64个采样段,每个段的采样点在过完\(N_c\)之后,进行渲染的过程中都会根据透明度计算权重(与光线击中此点的概率有关)。此权重可以作为\(N_f\)输入采样的指导。具体方法如下图所示:
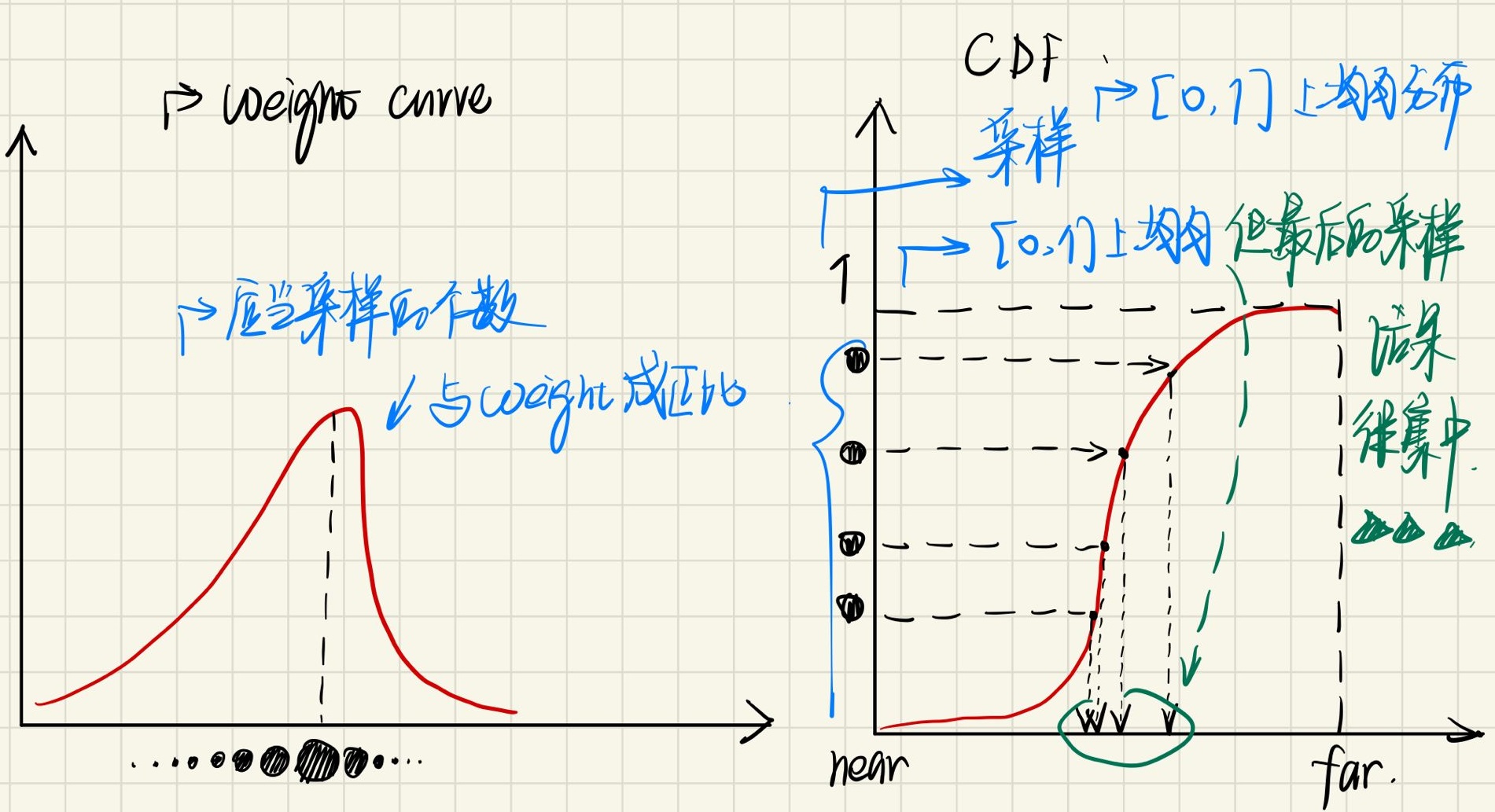
可见,\(N_c\)如果可以正确学习,在障碍物周围形成较高的不透明度(opacity比较大),normalized weight在障碍物周围形成的【障碍物CDF】就会类似于阶跃函数。那么当我在[0, 1]区间上进行均匀采样(采样不同weight的点),那么根据CDF曲线反查找到的length,都会集中在障碍物附近。CDF越类似一个阶跃函数,那么逆变换采样的点将越集中。不过注意,为了快速逆变换采样,near bound到far bound的分段最好是有序的:
- 在CPU上实现时,有序意味着可以二分查找,根据输入的weight,以及weight到length的映射表,便可以查找对应的length
- 在GPU上实现时,不可以使用二分查找。二分查找逻辑性强于计算性,CUDA实现将引起大量warp divergence,损害GPU并行度。不过即使是顺序查找,实现也还算简单,并且有效率:
1 | extern __shared__ float data[]; /// length: output_pnum + 6 |
代码如上。由于最终需要输出128个点,而\(N_c\)的分段是64份,为了避免数据拷贝时的warp divergence,在将数据加载到shared memory时,进行padding:原本64个分段,只需要存储64个length(float),但由于在我的设计中,一个线程采样一个点,128个线程如何复制64个float?必然有线程什么都不能做,比如:
1 | if (threadIdx.x < 64) |
此处就已经引入warp divergence了,虽然可能并不严重。如果考虑到将shared memory扩大到128个float,每个线程都可以复制到自己id对应的shared memory区,就不会有warp divergence现象。此外,由于64B对于 shared memory来说真的不是什么开销,所有线程一起执行时,多余的64次复制操作不会增加时间开销(怎么说呢,可能这只是我的一厢情愿,毕竟这个实现,没有绕开bank conflict),最多就是增加功耗,所以这样做也无妨。
此后,我只需要遍历大小为64的有序数组。当前采样weight小于length的部分全部使得计数器+1,便利结束之后,就可以知道自己在哪一个区域。这样的实现完全没有warp divergence,但是bank conflict就另说了。不得不说,这么看来我的GPU编程技术还是很菜,要想设计完美的GPU程序,还是需要更丰富的经验。(所以Instant-NGP 5s NeRF训练是真的牛逼)
2.3 获得采样点
对于NeRF在采样环节得到的光线,每条光线上所有的点最后生成的RGBA值都只会参与所在光线的监督学习(也就是说,不会被投影到别的视角下),故在确定光线以及采样点之后,就不再需要图像位置、相机参数等等信息了。
首先,如何在针孔相机假设下,通过焦距以及图像位置获得相机坐标系下的光线方向?纯针孔相机模型十分简单:
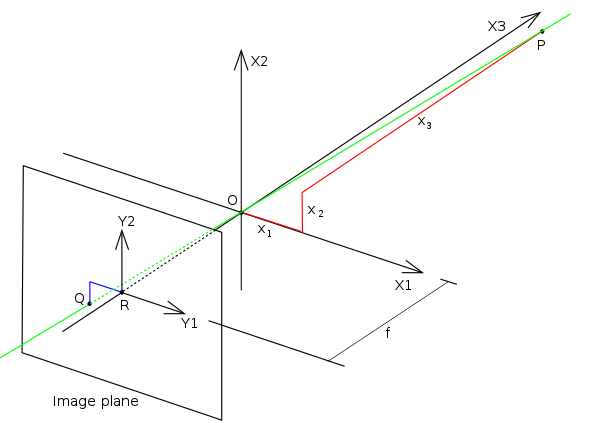
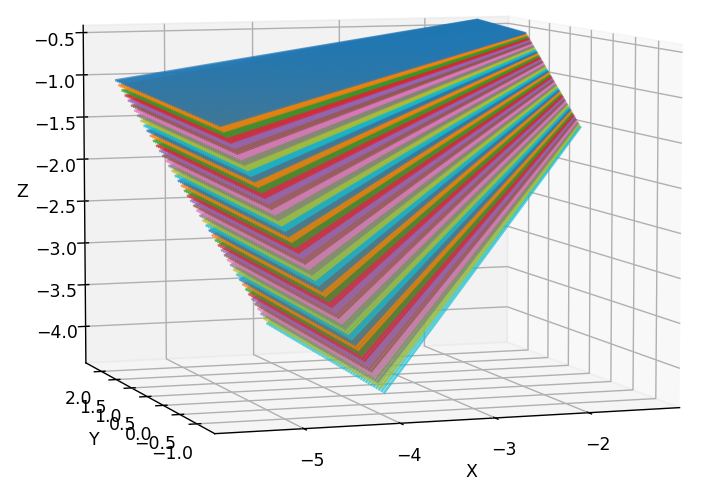
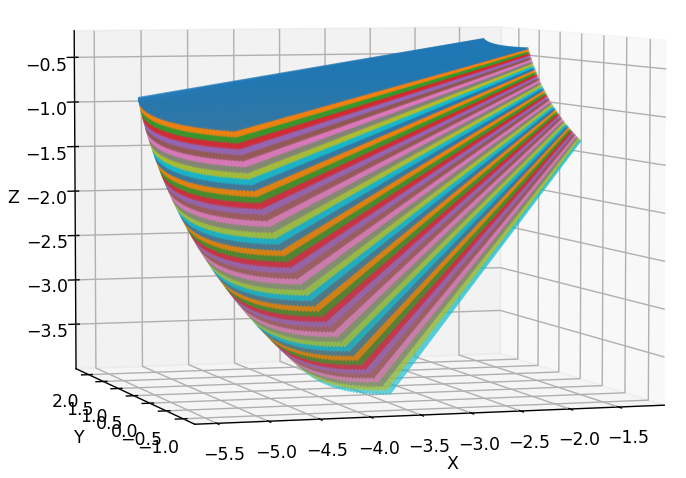
归一化相机坐标系下的光线方向与像素坐标之间的关系为: \[ \begin{equation} \begin{pmatrix} f & 0 & W/2\\ 0 & f & H/2\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} X_{\text{normed}}\\ Y_{\text{normed}}\\ 1 \end{pmatrix}= \begin{pmatrix} u\\ v\\ 1 \end{pmatrix} \end{equation} \] 那么只需要将上述公式取反,就可以轻松得到 \(X_{\text{normed}}=(u-W/2)/f\) 以及 \(Y_{\text{normed}}=(v-H/2)/f\)。我们通常讨论的相机模型因为有镜头,内参中的\(f\)一般都不是实际焦距,而是实际焦距乘以轴放大系数。在NeRF blender数据集中,焦距仅由FOV给出,没有其他内参系数,故知使用的相机模型是最简单的针孔模型。此外,注意COLMAP以及与之相关的数据集的光轴定义相对于标准相机坐标系而言,y以及z轴取反(体现在外参上,如果我们不做y,z轴取反的话,外参就是错误的)。故最后光线方向应该被表示为: \[ \begin{equation} \begin{pmatrix} (u-\frac{W}2)/f\\ (\frac{H}2-v)/f\\ -1 \end{pmatrix} \end{equation} \] 获得光线方向之后,注意不要归一化。归一化光线的方向向量 只在positional encoding前进行。过早地归一化,会使得一个梯台形frustum,成为一个... 具有弧度的形状,如下图所示。我们认为,梯台形frustum更加符合标准相机模型。
| 正常梯台frustum | 弧形frustum |
|---|---|
 |
 |
NeRF采样点需要在一个全局坐标系下(显然,否则都在自己的相机坐标系下,学习的内容将会有冲突)。故光线方向需要根据外参转换到世界坐标系。光线方向直接左乘外参的旋转分量即可。此后只需要根据方向,分段以及噪声抖动进行采样:
1 | sampled_coords = coords[indices] |
2.4 渲染
几乎所有关于NeRF的论文,在prerequisite部分,都会写原始NeRF的光线渲染公式。NeRF的光线渲染公式是由图形学的volume rendering积分公式得来的,但由于积分没有更简单的解析形式,只能使用累加进行近似。我并不是特别明白其中使用指数函数的原因(1984年的光线渲染原文也没有看得特别明白),但是如果将指数函数理解为任意增函数,其实渲染公式也很好理解。 \[ \begin{align} &C(\pmb{r})=\sum^N_{i=1}T_i(1-\exp(-\sigma_i\delta_i))\pmb{c_i}\\ &T_i=\prod_{j=1}^{i-1}\exp(-\sigma_i\delta_i)=\exp\left(\sum_{j=1}^{i-1}-\sigma_i\delta_i \right) \end{align} \] 其中\(\delta_i={t_{i+1}-t_{i}}\),也就是相邻两个采样点之间的距离,\(\sigma_i\)是计算的volume density(不透明度因子)。那么从采样点i到采样点i+1之间的透明度,被建模为:\(1-\exp(-\sigma_i\delta_i)\),可以看出,不透明度或者两点间距离越大,最后得到的透明度越低。透明度越高,到达i+1采样点时,i+1采样点的RGB将被更多地保留。那么\(T_i\)则是一个概率因子,此概率因子考虑了遮挡关系:假设光线在经过靠前的采样点时,通过了不透明度较高的区域,那么这条光线击中后面点的概率,应该降低。我们不能抛弃此概率因子而完全使用透明度。考虑这样的一个场景:
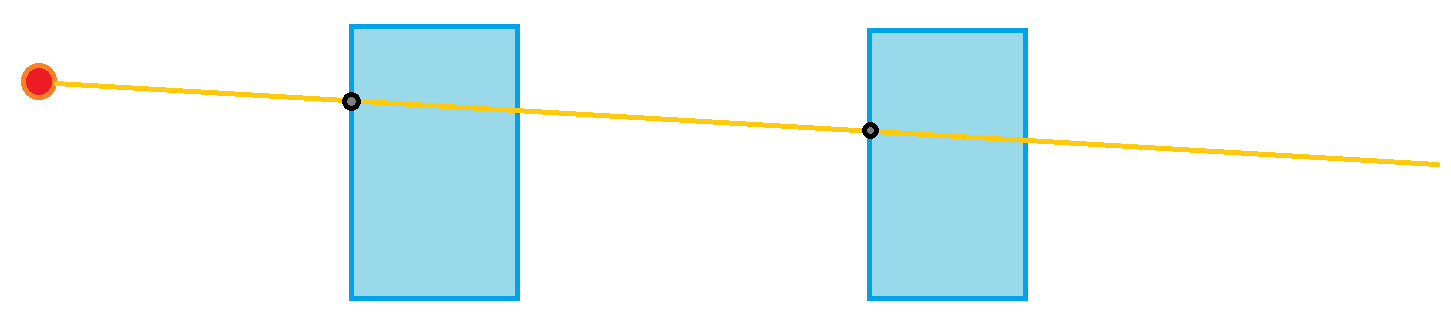
假设采样点只有这两个,两个物体的不透明度都较高。不考虑遮挡关系时,由\(1-\exp(-\sigma_i\delta_i)\)计算得到的透明度是相对比较接近的,这样就会造成两个不同物体RGB值的平均,得到错误的结果。\(T_i\)则可以解决这个问题。
渲染的实现并没有什么好讲的,根据公式实现就行。
2.5 杂项
粗网络使用的采样点,同样需要放入精网络中,与精网络的逆变换采样点合并。但是需要注意,渲染 一定要保证输入点以及深度值有序,根据渲染公式中的\(\delta_i=t_{i+1}-t_i\)就可以知道。故合并粗网络、精网络采样点之后,需要sort。怎么说呢,PyTorch对张量sort的支持,可比modern-gpu CUDA库的merge sort快多了...
curand_init,如果需要使用,首先需要引用头文件<curand.h>以及<curand_kernel.h>,此外,其四个参数中,有三个比较重要:seed subsequence offset randomState 不同的block以及线程可以根据其id直接获得不同seed 没用 别忘记设置,假设每次使用的randState都在kernel中被new出来,如果不根据函数执行的次数设置offset,每次的randomState都会是一样的 48位,还挺大,建议分块new,节省内存。详情见 deterministic_sampler.cuNeRF数据集非标准pytorch数据集,数据集加载需要自己实现。首先需要实现一个Dataset类(继承torch的相关类),其中必须要自定义
__getitem__函数(相当于C++中的[]运算符重载)。有Dataset类之后,就可以使用Dataloader了,torch的dataloader有两个好处,一是可以通过多workers的方式提高加载数据集的吞吐能力,使得加载数据集的耗时被掩盖。此外,dataloader非常节约显存,不需要一次性全部加载存在显存之后索引,笔者非常推荐这种方式。
III. 复现结果
舒服啦。debug之后还算成功,唯一不爽的就是 debug耗时太长,以为是什么重要的细节实现出错,最后竟然可能败在了positional encoding没有cat原输入上...
关于实现的依赖项,见Github项目的README.md。其中使用到了APEX加速,O2等级优化(实测,O3等级优化使得我的loss从一开始就是NaN,非概率性NaN)。O2优化的速度已经很快了,相对于原始无混合精度加速而言,已经加速了40-50%。12.5s可以跑完100次训练。在这里,一次训练包括:粗网络采样,1024条光线+64个点/每条光线-->
粗网络训练 --> 粗网络渲染 --> 逆变换采样 128点/每条光线 -->
精网络192点/每条光线 进行训练 --> 精网络渲染。速度还行,但对比起5s
NeRF... 太拉了。
我没有什么耐心,不想看到最后训练得有多好,只要有个可以的结果,就说明复现成功,对论文的理解充分:



Loss的变化曲线(drums)训练结果
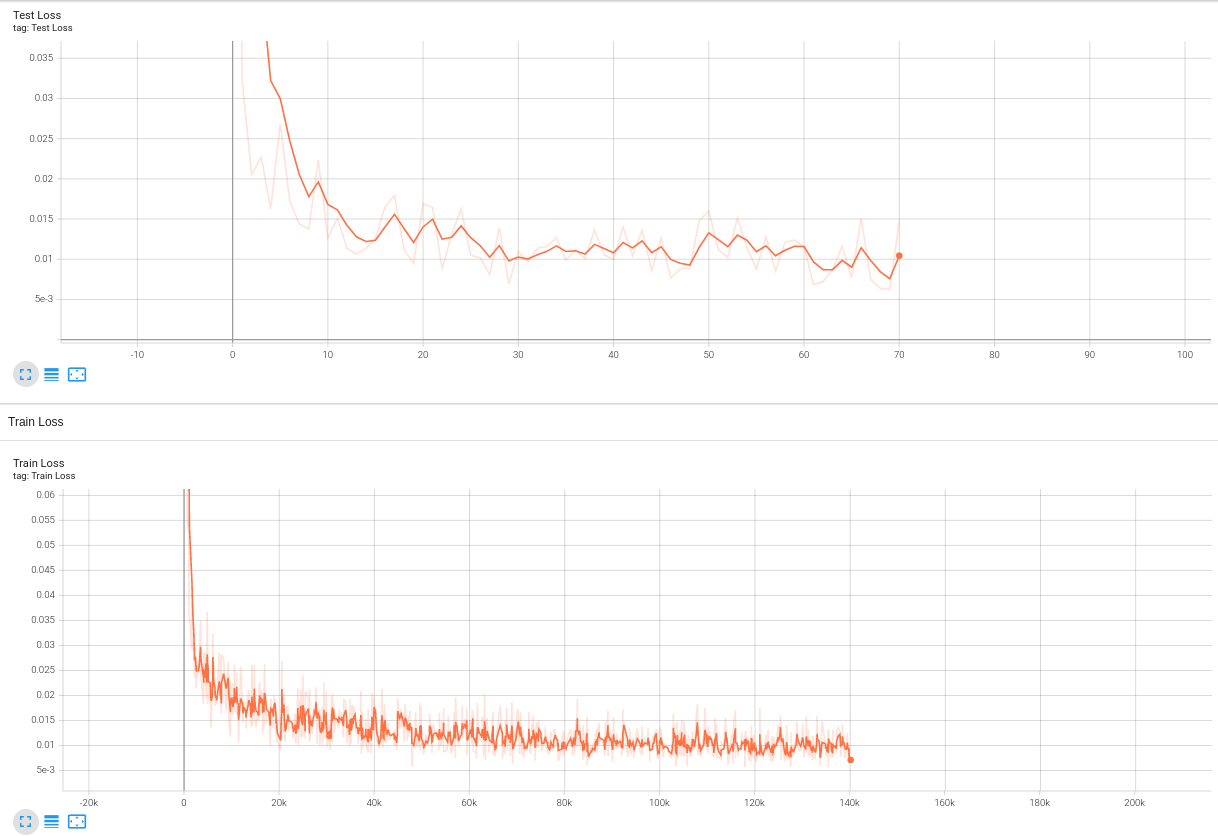
一些有趣(失败训练结果)的图:
| 好看的lego烧杯 | lego彩虹 | 更好看的lego云 |
|---|---|---|
 |
 |
 |