Ref NeRF复现

Posted on Edited on In Views: Symbols count in article: 15k Reading time ≈ 14 mins.

Ref NeRF复现

I. Intros

​ 科研恢复性训练。之前把CUDA加速的全并行shadow caster写完了，算是复习了CUDA、Rust以及FFI的使用。深度学习方面就以复现Ref NeRF为一个小任务。论文CVPR 2022 Best Student Honorable Mention: Ref NeRF - Structured View-Dependent Appearance for Neural Radiance Fields对反射现象进行了良好的建模。之前我一直在研究折射现象的NeRF建模，就折射建模思路而言，此文对我有很大的启发。并且个人认为，基于Ref NeRF以及mip NeRF作为框架是比较好的选择（除此之外就是要考虑如何让训练变快了，Instant NGP当然是不二选择）。当然，由于在复现过程中也遇到了许多问题，本文在阐述复现思路以及论文理解的同时，也会探讨踩过的坑。目前，Ref NeRF的复现结果还没有达到令我满意的程度，只是具备雏形，毕竟融合两篇文章的idea可能导致冲突，深度学习这种玄学就更是这样了，模型炸了都不知道从哪一个先开始。复现见 Enigmatisms/NeRF

Figure 1. Ref NeRF半成品(Shinny Blender - Helmet)。从左至右：RGB、depth与“奇怪的法向量”

II. 论文梳理

2.1 Ref NeRF的建模

​ Ref NeRF建模了表面反射，此工作比之前所看过的一篇处理反射的NeRF（NeRFReN）更有价值。个人认为，Ref NeRF可以被认为是一个不完整的光线传播模型，较好地解决了反射问题，只需要加上折射部分就可以使得NeRF处理基本的光线传播现象。本文对Ref NeRF的主要思路进行梳理，并且基于笔者对本论文的理解，在之前实现的NeRF（mip NeRF 360）基础上，增加Ref NeRF模块。

​ Ref NeRF处理的首要问题是光线的反射问题，反射一般分为两种：镜面反射（specularity）以及漫反射（diffusion）。那么根据Phong反射模型（以及之前学过半吊子图形学基础），被观察到的光线（强度）将为： \[ \begin{equation}\label{phong} I_o=k_aI_a+\sum_{i}k_d\left( l_i\cdot n\right)I_i+\sum_i k_s(r_i\cdot v)^pI_i \end{equation} \] ​ 其中，下标为a的部分与环境光（ambient light）有关；下标含有d则与漫反射有关，而下标含有s则与镜面高光有关。为了更好地解释Ref NeRF的反射模型处理以及回顾一下Phong模型这个基础模型，这里对公式\(\eqref{phong}\)模型简单解释：

  • 第一项代表环境光对观察结果的影响：环境光只对结果产生常数offset
  • 第二项代表了所有光源在物体上产生的漫反射。漫反射与观察方向无关，只要能观察到，就是“恒定”的。光源i (\(l_i\)为其发射的某一光线的方向）发射光越是能垂直表面（与法向平行），漫反射越强。
  • 第三项代表了镜面高光：不一定是完全的镜面反射（所以称之为镜面高光），可以稍显模糊，但是其强度是与视角有关的。\(r_i\)代表了反射光线的方向，\(v\)则代表了观察方向。两者重合（点乘结果接近1）时，反射较强。指数p用于加强衰减，可知p越大，\((r_i\cdot v)^p\)变化越快。也即视线与反射方向重合发生变化时，镜面高光的变化越明显。

​ Ref NeRF对于后两个部分都进行了建模： \[ \begin{equation}\label{ref} L_{out}(\hat{\omega_{o}})\propto \int L_{in}(\hat{\omega_{i}})p(\hat{\omega_{i}}\cdot\hat{\omega_{r}})d\hat{\omega_{i}}=F(\hat{\omega_{r}}) \end{equation} \] ​ 其中\(\hat{\omega_{o}}\)是观察方向（相机到物体），\(\hat{\omega_{i}}\)是光线的入射方向（光源到物体），\(\hat{\omega_{r}}\)是观察方向在物体上的反射（可以认为是相机按照\(\hat{\omega_{o}}\)方向发射光后反射的方向）。那么显然，\(\hat{\omega_{i}}\cdot\hat{\omega_{r}}\)就是公式\(\eqref{phong}\)中的 \(r_i\cdot v\)。在此工作中，函数p等均是神经网络（学出来的反射，强），并且作者强调，此函数就是反射方向 \(\hat{\omega_{r}}\)的函数（内部包含了观察视角方向信息）。反射方向的求解非常简单，这里不赘述。不过我不禁思考，如果把作者的反射模型从Phong模型换成Bling Phong模型会怎么样？在复现中笔者进行了尝试，结果见实验部分。

​ 作者花大力气改造原始NeRF的directional MLP，spatial MLP则只是输出了一些新的辅助信息。directional MLP必须要能够输出真正的view dependent颜色。作者认为：spatial MLP也需要直接预测颜色，但是此颜色应该是受环境光、漫反射等影响产生的（由公式 \(\eqref{phong}\)可知，环境光与漫反射均与视角无关），视角不变的颜色。严格来说，此部分颜色并非albedo（由于漫反射存在）。而directional MLP应当产生镜面高光部分。作者对directional MLP作了如下修改：

2.2 directional MLP修改

​ 首先，作者做了一个类似于mip NeRF中光锥处理的操作。mip NeRF中，为了达到mip map的效果，作者将点采样变为了光锥采样，以考虑整个光锥中的所有信息。Ref NeRF中，作者认为“反射”也不能仅仅考虑单个反射方向。由于物体实际是凹凸不平的，并非完美的镜面，表面法向量并非完全一致。可以认为，物体表面的凹凸起伏（噪声），使得反射发生了一些改变（distortion），物体表面噪声的概率分布，经过反射的数学操作后被映射成了新的分布。并且：

  • 新的分布应该是各方向对称的。由于我们并不知道物体表面能有什么样的各向异性特征。
  • 法向量分布的期望应该是 \(\hat{\omega_{r}}\)，也即根据求得的表面法向量以及观察方向求出的反射方向。其背后的intuition（总觉得，不应该翻译成直觉，故我这里用了一个英文单词，以表示：我觉得这里用中文表达不了那种意思）很好理解。
  • 法向量的方差应该受到物体表面粗糙程度进行控制。表面越粗糙，方差越大（法向量分布较广、分散）。这很符合现实。

​ 作者使用了一种叫做 von Mises-Fisher（简写为vMF）的概率分布。此分布的pdf非常像高斯分布pdf，估计也有差不多的性质。个人推测作者选这个函数是为了方便进行后续的数学推导以及近似，就像mip NeRF中，将光锥用混合高斯模型进行近似一样。有了此分布，自然需要使用积分将所有可能的反射方向考虑进去。当然不是直接求期望（求出来就是 \(\hat{\omega_{r}}\)，就直接trivial了）。考虑到，在将 \(\hat{\omega_{r}}\) 输入到directional MLP之前，需要进行positional encoding。在mip NeRF中，positional encoding参与了积分，在此处实际上也类似：我们需要在高维空间中求每一维度的期望。但作者并没有用sinusoidal positional encoding，而是使用球谐函数（spherical harmonics）对方向进行表示。最后对每一维球谐函数进行积分： \[ \begin{equation}\label{sphere} \mathbb{E}_{\hat\omega\sim{\text{vMF}(\hat{\omega_{r}},\kappa)}}[Y^m_{l}(\hat\omega)]\approx \exp(\frac{-l(l+1)}{\kappa})Y^m_{l}(\hat\omega) \end{equation} \] ​ 其中，\(\kappa\)为表面粗糙度的倒数（此值越大，越光滑），\(Y^m_{l}(\hat\omega)\)表示球谐函数（m，l都表示了其阶）。不难从公式\(\eqref{sphere}\)看出，积分近似后的球谐encoding实际上多了一个系数，此系数受到球谐阶（频率的指数）以及表面光滑程度（\(\kappa\)）的影响。显然，\(\kappa\)越小，对于高阶（频）球谐影响越大。这也就反映了这样一个事实：光滑程度减小，高低频信息均有所衰减，但高频信息衰减更严重。通过 \(\kappa\)就能直接影响输出结果中镜面高光的强度（模糊性以及保留细节多少）。

​ 当然作者不仅仅给directional MLP提供了\(\hat{\omega_{r}}\)，如公式 \(\eqref{phong}\)所示第二项的\(l_i\cdot n\)也被传入网络（\(d\cdot n\)，d为观察方向，n为法向量），这并不是要建模漫反射，而是考虑到一些稍微复杂一些的效应，如菲涅尔效应（并非全反射，部分反射部分折射，反射所占的比例需要另外计算）等等。

2.3 法向量估计

​ 作者使用volume density的梯度可以估计法向量，但作者说：

  1. normal vectors estimated from its volume density gradient as in Equation 3 are often extremely noisy
  2. NeRF tends to "fake" specular highlights by embedding emitters inside the object and partially occluding them with a "foggy" diffuse surface

​ 确实，（1）很显然，已经有很多论文做这方面的工作了，不是添加正则化项就是采用一些表面重建技术获得好的表面。（2）的话通常也是由“集中性”正则化项解决的（只不过作者的想法不太一样）。

  • 问题（1）的解决（prediction penalty）：通过spatial MLP预测某一点的法向量\(\hat{n}\)，与梯度法向量\(n'\)求MSE： \[ \begin{equation} L_{n}=\sum_{i}w_i\Vert \hat{n}_i-n'_i\Vert \end{equation} \] 由于\(\hat{n}\)相对比较光滑，而\(n'\)是对不光滑的density求的一阶导，就更不光滑了。用光滑数据帮助不光滑的梯度进行学习，可以起到对梯度的光滑作用。但为什么\(\hat{n}\)比较光滑？这是作者说的，其实我比较纳闷，毕竟这玩意是学出来的。我的理解是：可以认为，此处需要网络也同时将\(n'\)学出来（利用\(n'\)作为监督）。但是网络的表示能力有限，特别是参数较少时，只能达到对\(n'\)低频部分的学习。

  • 问题（2）的解决（orientation loss）：作者设计了一个正则化项：此正则化惩罚反向法向量，也即“背面”。但也不是盲目对背面进行惩罚，毕竟volume sampling过程中是可以在有效的背面进行采样的，故用下式： \[ \begin{equation}\label{reg} R_o=\sum_i{w_i\max(0,\hat{n}_i\cdot d)} \end{equation} \] 其中 \(w_i\) 为点weight值，\(d\)为光线方向。此处也即惩罚 法向量与光线方向相同部分。并且与weight有关，这就说明：被遮挡的有效背面不会被影响（weight低），而fake surface（在半透明surface后的embedded emitter表面）将会被惩罚（其density衰减方向与光线方向一致）

​ 作者自己也解释了一下，为什么这两个loss结合在一起就work了：网络对于法向量的预测（\(\hat{n}\)），与density梯度对应的法向量\(n'\)之间的关系大致有两种：

  • \(\hat{n}\) 偏离 \(n'\)。那么此时，prediction penalty较大，网络偏向于使得两者相等，则可以达到平滑梯度的目的。
  • \(\hat{n}\) 很接近 \(n'\)。那么此时，由于 \(\hat{n}\approx n'\)，我们可以认为公式\(\eqref{reg}\)作用在\(n'\)上。这也就达到了惩罚的目的。

2.4 扩展知识

2.4.1 一些物理概念

（1）能量，功率与辐射通量

​ 能量的单位一般采用（J），而功率则是单位时间内的能量（J/s，定义为W），此概念与通量（flux）是同一个概念。与接收能量的面积没有关系。

（2）辐照度与辐出度

​ 辐照度（irradiance）与辐射度（radiosity）是两个类似的概念，与面积有关。单位面积的通量（或者说，功率），单位是：\(W/m^2\)。注意，此面积是光照的“正对面积”，也即需要进行投影处理。当表面法向量与光线入射（出射）方向垂直时，辐照度以及辐射度最大。当然，以上讨论仅限于面平行光源。对于点光源而言，其辐照（射）度与距离的关系遵循平方反比定律（距离越远，辐照（射）度越低）。

（3）立体角与辐射强度（intensity）

​ 立体角表达的物理意义是：1立体角对应在单位球上截取的大小为\(r^2\)，其中\(r\)为球的半径。也即： \[ \begin{equation} \Omega = \frac{A_{sr}}{r^2}{\text{sr}} \end{equation} \] ​ \(\text{sr}\)是单位，而不是变量或常量。其中\(A_{sr}\)则是对应大小的球面切片面积。有了立体角之后，可以使用立体角 + 3D点 + 3D方向来描述任意光线。光线从给定的3D点出射，方向是给定的3D方向，光锥的形状由立体角确定。通过单位立体角的辐射功率（通量）称为辐射强度，单位是\(W/\text{sr}\)。辐射强度描述的是光源的属性，而非空间中某一点受光照的特性。故给定某一光源，不考虑空间中的其他因素的影响，空间中任意一点的辐射照度都是一样的。

（4）辐射率（radiance）

​ 搞NeRF也有一段时间了，还没有搞清楚radiance的意义。此前只是将radiance当作是观察到的物体的颜色，而现在这里将对辐射率的物理含义进行介绍。上文已经介绍了辐射强度的概念，并且可知，辐射强度与空间特性无关，只与光源有关，而我们又希望获得某一光源在空间中某一位置可产生的影响。则定义辐射率：单位时间、单位面积、单位立体角通过的光能。也即单位面积、单位立体角的功率。单位是：\(W(m^2 \text{sr})^{-1}\)。光源辐照能力改变（如灯光的亮暗），反映于功率变化（\(W\)）。而光源的“能量聚集度”（可以想象一个可以调焦的手电筒）反映在辐射强度上（影响单位为 \(\text{sr}\) 的项）。物体距离光源的远近则反映在面积项上（平方反比）。这也恰好与成像结果直接相关，故可以将radiance理解为空间中一点成像的结果（如RGB值）。

2.4.2 光场

​ 四维光场是否只是一个近似？四维光场认为，在empty space内部，radiance（也就是产生的RGB值）是恒定的。也就是说，无论我从此光线上的哪一点开始积分，最后得到的RGB值都是一样的，此RGB值与光线上的积分距离（或是深度）无关。那么这样可以从五维的光场建模中，去掉一个维度，实际则为四维的。个人更愿意将“四维”理解为一个五维空间中的四维流形，因为此深度维度并非五维度基中之一，也不能用其线性组合描述。理解了四维光场的由来，我们回头检查一下假设：空域内部radiance为常数。正常情况下：无半透明物体或者介质，这是成立的。引入半透明物体与介质后（比如混浊溶液，胶体，雾），个人认为此假设不成立，那么表四光场还是应该使用五维函数。

2.5 球谐函数的使用

​ 打开维基百科，查之。woc，我看到了什么。总之很复杂了，本人本科所学的数学知识不够用（或者说是遗忘了）。关于球谐函数本身的理解，个人的看法是：类似于傅里叶变换，展开成基函数的线性组合（这些基函数独立分析时其实形式较为简单，但组合起来就能表示非常丰富的内容），并且不像泰勒展开（泰勒展开的物理意义不甚好理解），球谐函数有频率概念，并且三维空间中的球谐函数仍然很好理解，非常具有物理直观性。如果想要知道如何初步理解，这里推荐【知乎：球谐函数介绍（Spherical Harmonics）】，我就不赘述了。下面只给出结论，实球谐函数的形式如下： \[ \begin{equation}\label{real_sh} Y_{lm}(\theta,\phi)=\begin{cases} (-1)^m\sqrt{2\frac{(2l+1)}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}}P_l^{|m|}(\cos\theta)\sin(|m|\phi), \text{ if }m <0\\ \sqrt{\frac{2l+1}{4\pi}}P_l^m(\cos\theta),\text{ if }m=0\\ (-1)^m\sqrt{2\frac{(2l+1)}{4\pi}\frac{(l-m)!}{(l+m)!}}P_l^{m}(\cos\theta)\cos(m\phi), \text{ if }m >0\\ \end{cases} \end{equation} \] ​ 其中，\(\phi,\theta\)是方位角（azimuthal angles），\(l,m\)为此球谐函数的阶？（此处实际上涉及到一个微分方程求解问题，此二变量与解的个数有关）。另外，比较令人疑惑的是 \(P^{|m|}_l\)，这实际上代表的是伴随勒让德多项式（associated Legendre polynomials）。这里，Wikipedia会告诉你勒让德多项式的奇妙性质，但是我不关心（说实在的，一开始看到这样的公式我还在想应该如何高效实现这么多微分）。这里直接给出维基上写的闭式公式： \[ \begin{equation}\label{legendre} P^m_l(x)=(-1)^m\cdot2^l\cdot(1-x^2)^{m/2}\sum^l_{k=m}\frac{k!}{(k-m)!}\cdot x^{k-m}\cdot \pmatrix{l\\k} \pmatrix{\frac{l+k-1}{2}\\l} \end{equation} \] ​ 此公式的代码实现就简单多了，我们只需要关心最后的求和项。求和项中涉及到求组合数，可以选择使用lookup table，预先计算一个大小为 \(2^L\cdot 2^L\)的矩阵（L应该不会很大）。那么： \[ \begin{equation} \frac{k!}{(k-m)!}\cdot x^{k-m} \end{equation} \] ​ 应该如何计算？能不用for循环就不用for循环（多用GPU操作！！）。观察容易知道：求和项中的首项是\(m!x^0\)，此后每一项与前一项的关系是： \[ \begin{equation} T_{k+1}=T_{k}\cdot x\cdot \frac{k+1}{k+1-m} \end{equation} \] ​ 故我们应该有这样的一个张量（一行，\(l-m\)列）：第一列是 \(m!\)，此后所有列是：\([\frac{m+1}{1}x,\frac{m+2}{2}x,\frac{m+3}{3}x,...,\frac{l}{l-m}x]\)。那么实现就是：

1
2
3
4
# device 某个传入函数的张量t的t.device
rare = (torch.arange(m+1,l+1, device = device) / torch.arange(1,l-m+1, device = device)).unsqueeze(0) * x
whole = torch.cat([torch.ones(1, 1, device = device) * m_factorial, rare], dim = -1)
whole_prod = torch.cumprod(whole, dim = -1)

​ 此后，根据lookup或者在线求解公式\(\eqref{legendre}\)中的组合数，就能求得求和式中的每一项，进而也就求出了整个多项式。但这只是针对 \({m,l}\)求出了结果，而 \(m,l\) 如何进行并行计算我就不懂了。不过其实也没必要懂：

  • NeRF的positional encoding，不同的相位（\(\sin,\cos\)）以及不同的频率是串行计算最后concatenate的
  • 大可以自定义CUDA算子，写一个forward再写一个backward函数。forward好写而backward不好写罢了（这玩意显然是有闭式解的，推起来比较麻烦），故CUDA自定义算子：全并行但费脑子（哈，而且还不一定有pytorch快，例如之前我用thrust的sort库对比pytorch的张量sort，前者就比后者慢），pytorch实现弱并行，但不费脑子。

​ 球谐函数的使用也说明了，我们在处理方向时，需要将三维的方向转化为二维的方向角（才能喂给球谐函数，当然，球谐函数确实有笛卡尔坐标系表示，但这不是我们的讨论范畴）。下面，笔者简单讨论一下文中球谐函数在vMF分布下的期望求解（论文附录部分）。作者要证明： \[ \begin{equation} \mathbb{E}_{\hat \omega\sim \text{vMF}({\hat\omega_r,\kappa})}[Y_l^m(\hat\omega)]= A_l(\kappa)Y_l^m(\hat\omega_r) \end{equation} \] ​ 我们只讨论上式中\(A_l(\kappa)\)怎么来的，而不关心（所以在这不推导）\(A_l(\kappa)\)如何近似为那个只与\(l,\kappa\)有关的指数形式（近似的推导部分，但凡有点耐心。。。emmm）。首先，作者把积分空间进行了线性变换：进行了旋转。将 \(\hat\omega_r\)旋转至z轴，那么根据vMF分布的形式以及随机变量函数的期望的计算： \[ \begin{align} &P_{\text{vMF}({\hat\omega_r,\kappa})}(\omega)=c(\kappa)\exp(\kappa\hat\omega_r^T\omega)\\ &\mathbb{E}_{\hat \omega\sim \text{vMF}({\hat\omega_r,\kappa})}[Y_l^m(\hat\omega)]= c(\kappa)\int_S Y_l^m(\omega) \exp(\kappa\hat\omega_r^T\omega)d\omega\label{expect} \end{align} \] ​ 则将 \(\omega'=R\omega\)中，可以得到： \[ \begin{align} \mathbb{E}_{\hat \omega\sim \text{vMF}({\hat\omega_r,\kappa})}[Y_l^m(\hat\omega)]&= c(\kappa)\int_S Y_l^m(R^{-1}\omega') \exp(\kappa (R^{-1}z)^TR^{-1}\omega')dR^{-1}\omega' \label{ints}\\ &=c(\kappa)\int_S Y_l^m(R^{-1}\omega') \exp(\kappa z^T\omega')dR^{-1}\omega' \label{intm}\\ &=c(\kappa)\int_S Y_l^m(R^{-1}\omega') \exp(\kappa \cos\theta)d\omega' \label{inte} \end{align} \] ​ 从公式\(\eqref{ints}\)到\(\eqref{intm}\)很好理解，旋转向量的的正交性可以立刻抵消exp中的R。而公式\(\eqref{intm}\)到\(\eqref{inte}\)则稍微有点绕：

  • \(z^T\omega'\)恰好是 \(\omega'\) 的方位角（中的俯仰角\(\theta\)）
  • \(dR^{-1}\omega'\)中的 \(R^{-1}\)原先需要被提出来，但由于其行列式为1（旋转矩阵嘛），不会影响最后函数输出的单个值的结果（注意，对于每一个\(m, l\)而言，公式\(\eqref{ints}\)的输出都是一个值），故可以省略

​ 此后，根据球谐函数的性质（比如展开为Wigner D Matrix表示以及其正交性），我们最后可以将公式\(\eqref{ints}\)左边写为： \[ \begin{equation} \mathbb{E}_{\hat \omega\sim \text{vMF}({\hat\omega_r,\kappa})}[Y_l^m(\hat\omega)]= c(\kappa)D^{(l)}_{m0}(\hat{\omega}_r)\int_{S^2}Y_{l}^0(\hat{\omega})e^{\kappa\cos\theta} d\hat{\omega}\label{origin} \end{equation} \] ​ 其中：\(D^{(l)}_{m0}(\hat{\omega}_r)\)以及\(Y_{l}^0(\hat{\omega})\)的形式都是已知的，这里不在赘述了（确实很麻烦）。我们只将上式的积分部分进行拆解。由于积分实际上是在球面上完成的，这里实际进行了一次二重积分（球面积分），将笛卡尔坐标系转化为球面的天顶角：\((x, y, z)\rightarrow(\theta,\phi )\)，这里给出一张图：

Figure 2. Ref NeRF半球积分示意图

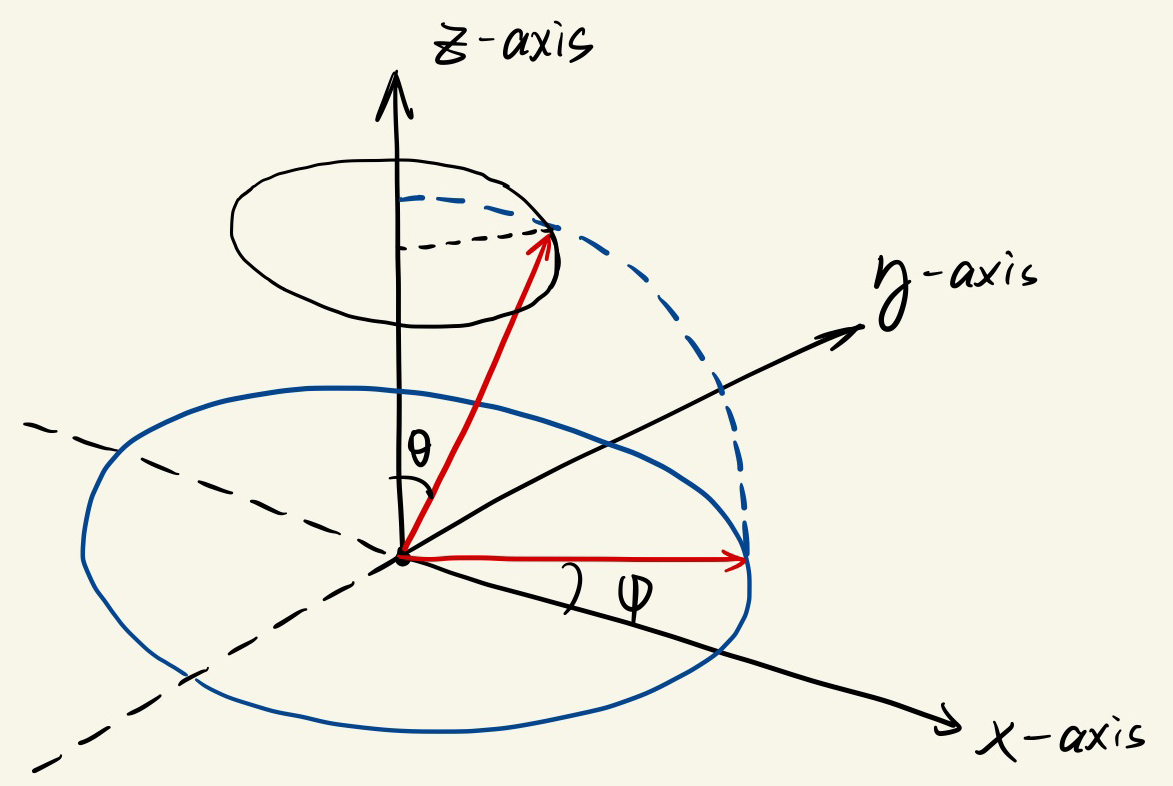
​ 图中的黑色圆圈就是“积分对象”：可以看做球体的上半球表面是由无数个圆环组成的，对应了角度为\(\theta\)（确定了位置），半径为\(\sin \theta\)（确定了形状）的圆圈（可知\(\phi\)的积分范围是\(-\pi\rightarrow\pi\)）：故积分可以拆成（首先知道\(Y_l^0(\hat{\omega})=P_l(\cos\theta)\)）: \[ \begin{equation} \int_{S^2}Y_{l}^0(\hat{\omega})e^{\kappa\cos\theta} d\hat{\omega}=\int_{-\pi}^{\pi}\int_{0}^{\pi}P_l(\cos\theta)e^{\kappa\cos\theta}\sin\theta d\theta d\phi \end{equation} \] ​ \(\theta\)的范围是\([0, \pi]\)，这是因为我们只需要积分上半球。由于反射不可能发生在下半球，可知下半球\([-\pi,0]\)的所有输出都是0。这样，根据论文中所说的步骤，进一步替换积分变量，展开并简化可以推出IDE公式。

​ 但是，选择实函数形式的球谐并不是一个很好的选择。首先，公式\(\eqref{real_sh}\)已经展示了实函数形式的复杂性（主要是有分支）；此外，我们需要考虑到，角度形式的SH需要把方向向量转化为天顶角，这种额外的操作看着就很不优雅。建议使用笛卡尔坐标系形式的球谐函数。参见Wikipedia/Shperical Harmonics - Separated Cartesian form，可刺激了，虚函数运算与二项式公式的结合哦。不过只要使用这种方法实现，利用Pytorch就很简单：

  • 首先Pytorch支持虚数运算。这里吐槽一下，Pytorch支持的虚数运算基于torch.complex64类型，一看到64就知道怎么回事了，运算量可能等同于float32运算（两个float32存在一块），在使用auto mixed precision时，complex32将可能产生一系列的问题，很多算子都没有对complex32有支持。而假设我们使用APEX库的O2等级优化，所有的float32都会变成float16，那么这里参与运算的复数就会产生一系列未定义算子的问题。（什么ComplexHalf未定义这些算子啊之类的报错）
  • SH在这就是用作encoding，所以其实只需要将结果的实部、虚部取出来作为encoding的成分就好了。可以认为，原来的positional encoding是用了正交相位的两种基底进行表示，而SH其实也是正交的两种基底（实与虚在虚平面上是正交的）进行表示。

III. 复现细节

3.1 值得一提的点

Figure 3. Ref-NeRF网络结构

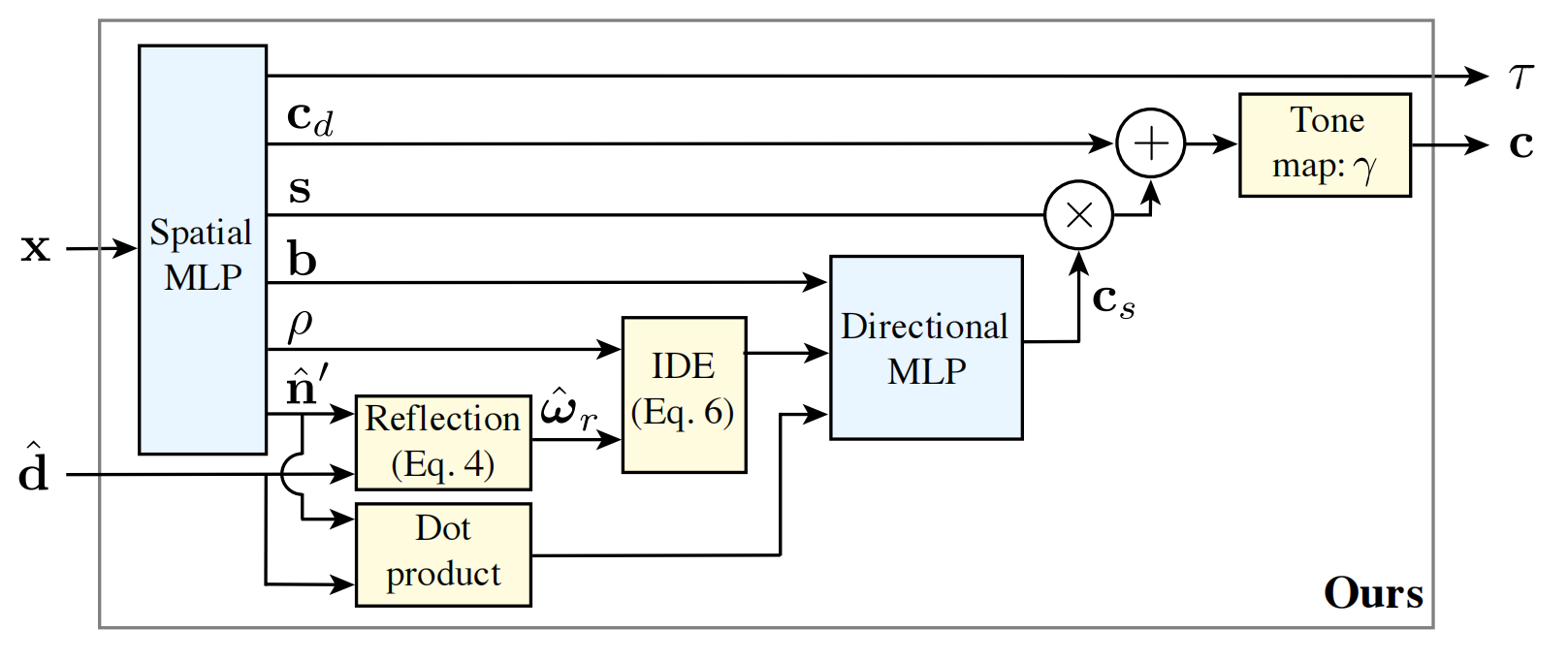
​ 其实，没什么好说的。根据Ref NeRF论文图，复现的内容如下：

​ 首先修改spatial network，在spatia network之后追加三个head。三个head的输入就是spatial network的输出：

  • opacity & roughness head: 由于τ（density）与ρ（roughness）都是没有输出范围限制的（但是都需要大于0，故ρ之后与τ类似，单独处理即可）。注意roughness与opacity都需要经过bias之后再通过softplus激活（软ReLU）

  • color & tint head: \(c_d,s\)都是[0, 1] 之间的值，故输出直接变6维。color与tint都使用sigmoid进行激活，不过bias不同。

  • normal head：预测法向量，三维，需要进行normalize，不需要任何激活

​ 需要绕一下的部分是法向量。法向量的来源有两个：（1）spatial network计算的density，可以对位置求导。Pytorch中，要实现对位置求导需要使得输入的位置向量可导：

1
2
3
4
5
6
fine_pos.requires_grad = True										    # 此步必要	
fine_rgbo, pred_normal = mip_net.forward(fine_pos, fine_dir)
r_num, p_num, _ = fine_rgbo.shape
density_grad, = torch.autograd.grad(fine_rgbo[..., -1], fine_pos, 			  # fine_pos 是可优化的
       torch.ones(r_num, p_num, device = fine_rgbo.device), retain_graph = True # retain graph使得计算图可以继续backward
)

​ 另一个来源就是spatial network之后的normal head，预测。预测的结果在经过正则化（orientation loss）以及预测误差（与density grad的差别）backward之后，应当可以学出较好的结果。

​ 此外注意，directional network变深了。可以认为directional network有spatial network一样的结构（包括8层256 hidden units的MLP，并且有skip connection）。

3.2 一些坑

​ 由于笔者复现Ref NeRF基于之前实现的Enigmatisms/NeRF，这个repo中实现的NeRF并非原始NeRF，而是mip NeRF 360（部分），主要包含这样的特性：

  • 本repo实现了mip NeRF 360中的proposal network distillation。也即：coarse-to-fine的stratified sampling并没有使用。stratified sampling非常慢（由于coarse network需要forward所有点，fine network也要forward），proposal network则是用浅MLP（5层），forward点后直接输出预测的density，再利用fine network输出的density（weight）进行监督。这样就能完成从fine network到proposal network的蒸馏。此蒸馏的实现较为复杂（weight bound的计算），这里不赘述。我也不想单开一篇博客讨论。
  • 使用了自动混合精度（amp），可以选用apex或者torch.native_scaler

​ proposal network着实坑了我一把。复现完成（第一版）之后，跑了一下shinny blender的ball数据集：

Figure 4. 为什么那么多噪点？

​ 如上图第一列：很多噪点。这些噪点是什么？一开始我也不敢下结论，毕竟不知道是不是自己的ref nerf复现有问题。于是我将深度以及normal都可视化了出来（后两列）。可见，深度图中也存在很多空洞，normal就不说了吧（事实上，normal学习一直有问题，normal本身就比较难学）。空洞产生的可能原因有两个：

  • density学习有问题，有些位置density非常低
  • 采样（不管是训练还是测试时）位置不对，采样在了一些空的位置

​ 于是我开了一个新的分支，在此分支上我将proposal network删掉了，使用原始NeRF的coarse-to-fine框架进行测试。对比图如下图所示：左边为原始proposal network存在时，训练60轮之后的结果，而右边则为原始NeRF训练40轮之后的结果。可以看出，原始NeRF框架下的采样是（至少相对上是）没问题的。但笔者并不想放弃proposal network（个人觉得这个方法比较优雅），故笔者将proposal network进行了小的改动：

​ 原始prop net输入coarse points之后，输出density，此后coarse points将会被弃用。根据density计算的weight，将指导inverse sampling，fine network的输入只为inverse sampling的结果（也就是说，集中在weight高的地方）。假设，prop net计算的density有缺陷，也即weight有缺陷，在实际的表面附近weight很小，在空域中weight大，那么inverse sampling可能无法在此条光线上采到有效的点。

​ 很简单，就是复用coarse points，将coarse depths（采样的长度）与inverse sampling的采样长度（fine depths）进行拼接，排序。但其实在实现中，要考虑proposal network的weight bound计算。啊，这一步很复杂。可以这么说：

  • proposal network需要预测每一个采样点（fine采样点）的weight上界（weight bound）。上界如何计算？两个fine采样点之间会存在一个采样区间，此区间将会与coarse采样的区间重合，则此fine采样区间的weight上界应该是所有与之有交集的coarse区间weight之和。
  • coarse points合并到fine points相当于修改了fine采样区间。那么就需要计算更多区间交集。这里我不赘述方法，详见：NeRF/coarseFineMerge以及NeRF/getBounds

​ 这样修改，也就使得每条光线上，既有均匀采样的部分（保证了coverage），又使得density大的部分可以有更多采样点。可能有人觉得，不就是增加了一些采样点吗？这样为什么能保证proposal network的学习是正确的呢？很简单，网络不仅有更加充足的输入，fine network提供给proposal network的监督也更加充足了（见【修改后的Proposal Network】部分，其中我们说到“更多的区间交集”）。

Figure 5. shinny blender helmet数据集，训练20轮
无proposal net 训练40轮（4k次） 有proposal net 训练60轮（6k次）

​ 修改后的方法，只训练20轮输出后的结果就让我觉得肯定是改对了，如上图所示。接下来将展示【未完成训练】时的训练结果。由于原始Ref NeRF使用\(2^{14}\)大小的batch，需要训练250k轮。我设备能力有限，只batch大小为\(2^9\)（差了32倍），也没训练到250k就先暂停了（笑死，我的3060 for laptop，有个风扇坏了，训练的时候能飙到83度，所以我得开一台电风扇对着我电脑吹）。下面是简单的结果展示：

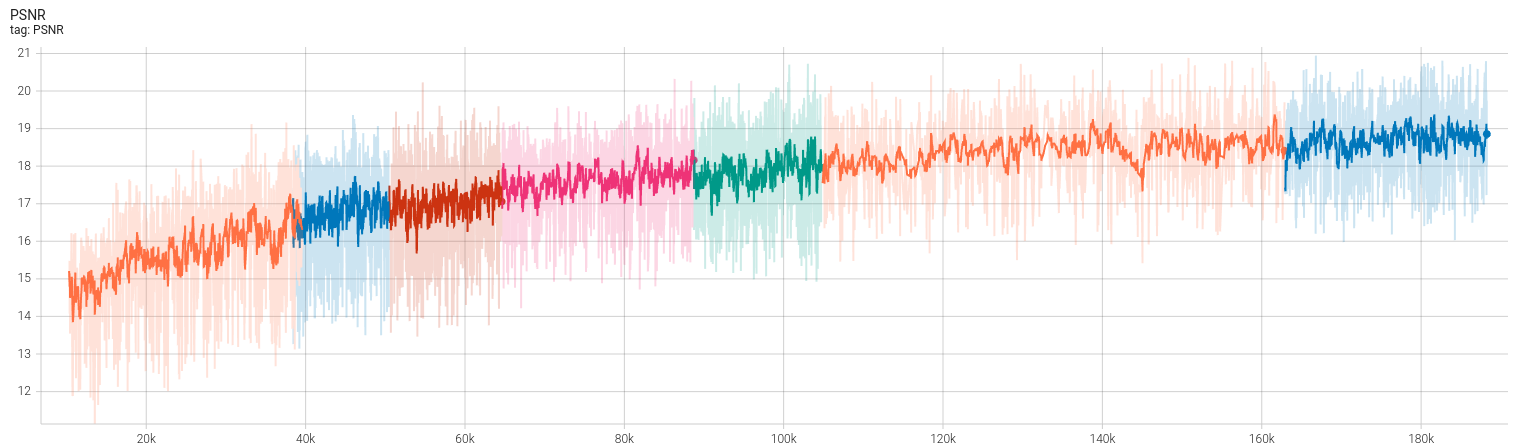
Figure 6. 训练不是一次完成的，保存checkpoint短点续训。收敛性并不好

​ 从上图看出，虽然训练应该远没有结束（这才不到7小时），PSNR曲线的上升能力属实堪忧。笔者感觉PSNR无法上升至论文中的29，个人认为可能的问题仍然是出在proposal network上。目前正在尝试一种改进的方法。

Figure 7. 有趣的手动退火

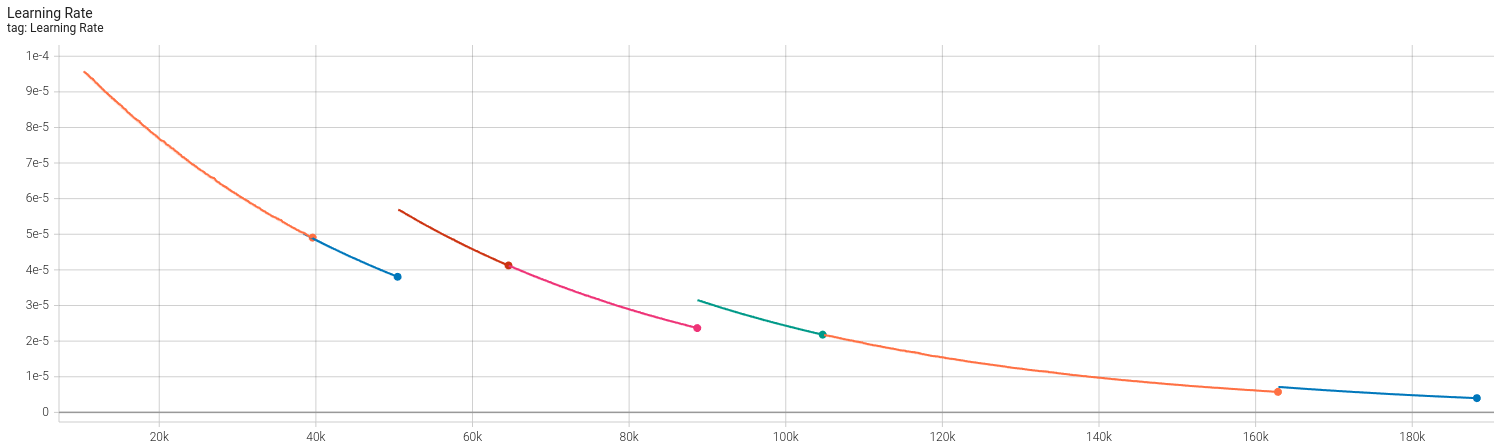
​ 效果大概就是这样（如下图所示）。从左到右分别是：RGB，深度与法向量。emm，法向量大概是可视化错了。不过学的应该也有一些问题，在某些视角能看到头盔上的条纹对应的法向量与其他位置不一致。PSNR为19，还是太模糊了一点。

Figure 8. 旋转头盔

Reference

  • https://en.wikipedia.org/wiki/Spherical_harmonics

  • https://en.wikipedia.org/wiki/Associated_Legendre_polynomials

  • 扩展阅读: https://dellaert.github.io/NeRF22/