Taichi-Learning-II

Posted on Edited on In Views: Symbols count in article: 13k Reading time ≈ 11 mins.

Taichi Lang II

I. Intros

​ 深入了解Taichi语言，简单的并行算法设计无法满足我（毕竟真要说并行算法设计，Taichi所需的工作量与CUDA暂时没办法比）。Taichi中重要的两个features：稀疏数据结构（SSDS），可微编程（differentiable programming）目前对我而言比较重要的就是SSDS，可微编程... 可微渲染可能可以用到，但是本身实在是太复杂了... 我一直觉得，不动手就学不到真正的知识，所以还是给自己布置了一道题，并且要求将SSDS以及在第一篇博客完成后学到的内容整合到此题的解答中。本文是最后一篇Taichi 入门博客，关于一些进阶的用法以及特性，以及在实现题目：flocking simulation（鸟群模拟）中所学到的一些知识。文末附有flocking sim的视频。

​ 预计我下一步将会使用Taichi写一个带有participating media功能的path tracer（3D，之前Rust + CUDA写了一个没开源的2D tracer，只能看光路，不能看渲染结果（毕竟是2D）），以加深我对光线追踪算法的理解。不过这是个大项目，简单版本的也至少涉及到mesh的读取、加载、光线弹射、采样、介质实现、蒙特卡洛积分等等... 想想就刺激。

frame 52 (红色为掠食者，白色为普通鸟) frame 58 (红色为掠食者，白色为普通鸟)
000052 000058
Figure 1. Flocking simulation with predators (64 regular boids (this is not a typo) and 4 predators)

II. Type System

2.1 Type System

2.1.1 Prerequisites & Casting

​ 其实这部分并没有太多可以说的，只有些零零碎碎的点需要提醒，我在实现的时候没有遇到太多有关类型的问题。首先需要说明的是，Taichi是静态强类型语言，所以类型不能乱来。虽然其撰写时的语法就是Python，但由于没有显式类型声明，类型推断以及隐式类型转换可能导致非常多的问题。首先说一下 type alias 以及一些入门级前置知识：

  • Type alias实际上是Taichi default types可以使用的别名，例如不进行特殊设置（ti.init时），float = ti.f32，int = ti.i32，float, int分别为ti.f32, ti.i32的 type aliases
  • Taichi有两大类类型：primitive types，就是基础类型，诸如f32, i32, u8等等，没有boolean type（用i32代替）。另一类是 compound types，也即复杂的数据结构：vector，matrix（vector就是matrix），ndarray以及struct（其实我现在都还没怎么用到ndarray）。上一篇博文中，我简要分析了一下field与ndarray的区别：ndarray不允许在kernel内进行非compile-time-known的indexing操作。这主要是因为，ndarray是compound type（具有明确的类型），而field不具有明确的类型（是一个复杂container）。

​ 此外，在上篇博客中忘记说了，我在开始学Taichi时曾经碰到这样的问题：

  • 教程中简单的examples全都将field设为全局变量。使用全局变量并不是好习惯，并且很丑（封装性很差）
  • 开始时我想将field作为参数传入kernel函数。但是遇到了type annotation的问题：我无法找到field的type定义：从我现在所学的知识来看，可能确实找不到，毕竟field不是两大类型中的任意一种。

​ 于是我觉得：说不定作者并不想让field传来传去呢？于是之后的三个小demo全部改成了使用@ti.data_oriented的class。但field无法当参数传递是个错误的想法，我犯这个错误是因为两天的入门学得太浅。此概念实际与Taichi metaprogramming关系非常密切，这里说到field的类型就忍不住跑了个题...，下面说说casting。

​ ti.cast可以执行类型转换（在compile time对某个变量强制赋予某个类型，以免implicit casting / type inference造成的类型错误）

​ 但是注意，此函数只能在ti.init之后使用，并且返回值并不是primitive types：

  • 返回值类型是ti.Expr（个人对Expr的理解类似Eigen库，表达式模板运算，惰性计算，compile），与下面所表达的意思比较一致：先生成类似表达式模板的东西（相当于知晓接下来要进行什么操作），并且由于Taichi对于platform敏感，乘法操作在不同的backend下实现可能不同，所以总是先生成一个Expr，Expr中的乘法操作会根据backend进行不同的调用。

来自这里: In fact, when you type x * 2, it’s not evaluated immediately. That’s why we need x to be Expr. What Expr express is not a value, but an instruction.

​ 在上一篇博客中，我也提到了Expr导致的一些误解（例如直接使用看似为integer的变量为什么无法直接indexing），个人觉得应该与惰性计算有一定的关系。故在kernel函数中，一般无法调用numpy等函数（计算张量、数值而非表达式运算），而Taichi函数有处理表达式以及立即数（可以理解为constexpr运算么）的能力。

  • ti.i32, ti.f64这样的操作也可以进行casting，并且由于int, float是对应的default types，故也可以直接使用作为casting方法，例如ti.f32(1)

​ Taichi中能type annotation的地方尽量type annotation，并且不要写得太像python（例如让解释器进行自动类型转换），该手动强制类型转换的地方尽量手动转：（1）隐式类型转换经常出问题（2）不出问题也有可能因为损失精度而在编译阶段报一堆烦人的warnings

2.1.2 Compound Types

​ vector以及matrix就不多说了，这里只提一个与性能相关的点，个人觉得有点坑（不看文档是不知道的）：

​ Matrix以及vector操作在compile时会进行unrolling：a = [[1, 2, 3], [4, 5, 6]]会成为对应index的赋值（刚学到这里的时候我觉得非常怪：明明是spatially neighboring的数据，这样不会影响效率吗？可以SIMD吗？答案是：确实会影响效率）

Operating on larger matrices (for example 32x128) can lead to longer compilation time and poorer performance. For performance reasons, it is recommended that you keep your matrices small. (So bad)

​ Struct这玩意，熟悉C的同志们应该并不陌生（？奇妙的逻辑）。但就我当前对struct的理解（涉及到advanced container的部分内容，如SoA以及AoS），想要追求性能机制时对于struct的使用需要慎之又慎：我们知道，struct存在的意义就是让数据更有组织，每个具名域表达一个清晰的含义，如：name, age等等。但由于struct在物理实现上是空间连续的结构，空间连续性以及内存的分页机制将产生一系列的问题，具体的讨论留到【第三节3.1 SoA vs. AoS】。我在这里说这个是想强调：按照我的理解，我并不推荐无脑照搬C/C++那一套封装数据一定就得上struct甚至class的思想。

​ 首先，如何创建一个high level compound type struct捏？

1
ti.types.struct(a = type_1, b = type_2, ...)

​ 其中，type_1以及type_2可以是primitive types或者compound types，注意上述代码返回了一个特定的类型（一个struct类型，而非struct实例）。由于struct也是compound type，struct的复合是可以的，但貌似struct的构造必须使用keyword arguments（即便按顺序，不使用keyword arguments，则需要将内部struct展开，比如看下面一个例子）：

1
2
3
vec2 = ti.types.vector(2, float)
inner_type = ti.types.struct(weight = int, center = vec2)
ball_type = ti.types.struct(desc = inner_type, radii = vec2)

​ 以上例子定义了一个椭球（由于radii是二维向量，意味着可以长短轴可以不同长度）。如果要进行构造，有两种办法：

1
2
ball_1 = ball_type(desc = inner_type(2, vec2([1, 3])), radii = vec2([0.5, 0.5]))
ball_2 = ball_type(2, vec2([1, 3]), vec2([0.5, 0.5]))

​ 第一种构造方法需要限定keyword arguments，直接这样构造是不行的：

1
ball_1 = ball_type(inner_type(2, vec2([1, 3])), vec2([0.5, 0.5]))

​ 会报如下错：

1
TypeError: int() argument must be a string, a bytes-like object or a number, not 'Struct'

​ 只能说很奇妙，与C++确实比较不同，C++就没有explicit keyword argument这一说。而ti.dataclass则提供了如同rust一般的struct定义方法：

1
2
3
4
5
6
7
8
@ti.dataclass
class Ball:
	@ti.dataclass
	class Inner:
		center: vec2
		radius: float
	inner: Inner
	weight: int

​ 使用冒号进行type annotate（当做type definition），这一点与Rust很像，此后不用任何其他方法（当做struct用就好了，实际上其类型也是Struct）。原始Python则不支持这么做：

1
2
3
4
5
class Test:
    	a: int
# test = Test(1)		 当然是会报错的
test = Test()
test.a							# 只留type hint的话，a当然是NoneType（没有定义，只有“声明”当然没有用）

​ 但很可惜的是，dataclass定义的struct（在Python中是带有@ti.dataclass修饰的class）并不支持继承，一定程度上限制了应用吧？（至少在我的flocking simulation中，我曾经想使用dataclass修饰类作为基类，但发现这玩意已经是final了），这个例子我在第三节会简单介绍一下。

III. Spatially Sparse Data Structure 实例分析

3.0 Background

​ 本节所介绍的内容为 Taichi 中最重要的部分之一，基础知识部分参见 Taichi Lang Docs: Data Containers。Taichi 做这样的设计有充分的理由：稀疏的数据结构（Spatially Sparse Data Structure - SSDS）需要有更加有效的并行操作实现。举个例子，笔者在研一上（也就是这个学期）时陷在CUDA中，因为写CUDA就像炒期货：风险巨大（调参困难，并且需要充分的内存、逻辑设计才能快）但可以给人一种巨大的成就感（前提是写出来能跑、结果对、速度快、能正确链接到Rust上进行可视化）。CUDA中就有两个重要的feature限制了稀疏数据结构的使用：

  • CUDA中的内存操作（这一点非常深，我也只能算门外汉）：比如memory coalescing (“have consecutive threads access consecutive memory addresses”[1]) 以及内存带宽优化等。要好理解的话，假设有一个C++ vector以及C++ deque存在GPU上，由于vector是连续内存，读取对内存操作是友好的（在CPU上也是，特别是有分页机制时）要基于vector做稀疏存储结构，则需要一定的辅助结构（如boolean flags）。而deque可以做到稀疏（由于其非连续读取，虽然iterator的使用隐藏了这一点），但分散的内存不便于内存操作的优化。
  • warp divergence：基于flag、bitmask等的数据结构可以通过判定某块区域是否valid达到对于invalid块不进行内存分配的目的。但在GPU代码中，判断应当尽可能避免（除非另一个branch是NOP），否则就会产生divergence serialization问题。

​ 强如Nvidia，设计出来的CUDA，也不是特别适合SSDS... 所以Taichi出手了。SSDS的应用广泛性不用多说，例如基于voxels的NeRF，强一点可以使用coarse-to-fine resolutions的层级voxels，弱一点的做一个empty voxel culling总是可以的吧？这些都涉及到将一个dense的内存块变为sparse的操作（或者是内存的分级管理），Taichi则有这样的API（或者内部特性）。

Figure 2. SSDS Taichi official examples: fluid particle / multi-res grid mixture representation simulation[2]

​ 光看文档是没用的（再次quote西交刘龙军老师的话：”读论文不复现等于白读“）。确实，读书与上课会给人一种你已经学会了的错觉，但停留于”知道了、了解了“等级的”学会“是没用的，只能用于吹逼；我们应当时刻追求”会用，深入实验了“等级的”学会“。所以我给自己Taichi入门级别学习定的最后一个作业是：Flocking simulation (Craig Reynolds' Boid Algorithm)。我很早之前就注意到这个算法了（当时才大四，在学Rust，苦于不知道用什么可视化库的时候），问题参考【Reddit: First rust program | flocking simulation.】，但我并不想去复现它。对于简单的算法，复现别人的复现（复现\(^2\)）并没有太大的意思，尝试用自己的理解写出算法才是有趣的事情。于是我只参考了其美术设计（确实，nannou看起来挺高大上的），用Taichi写了一个flocking simulation（可能与Craig Reynolds' Boid Algorithm不太像，毕竟我只用了其最抽象的思想，什么separation, alignment以及cohesion，具体这几个鸟群性质怎么实现都得自己设计）。我在本小项目中尝试使用SSDS加速邻近搜索（neighbor search），道理是挺有道理的，但没有做过profiling看具体的加速效果。

Boid: Bird-roids 或是bird的一种带有口音的读法。

Figure 3. Flocking simulation with multiple predators

3.1 SoA vs. AoS

​ Struct of Arrays（SoA）: 意思是一个struct中的变量是array（比如一个struct中有好几个数组），很显然对于struct中的每一个Array，内部元素都是空间临近的（直接邻近）。而不同array的内存可以分配在不同的位置，没有空间邻近性。

​ Array of Struct（AoS）的意思是：某个array的元素是一个struct。很明显，Array of struct中，单个struct内部的元素之间是空间邻近的（由于struct需要连续的内存区），而不同的struct element之间只有有限的邻近性，举个例子：一个struct中含有double a, double b , std::shared_ptr<xxx> c，那么即使是相邻的两个struct中的变量a都可能相距几十个字节。

​ 正如我在第二节时所说的：SoA与AoS需谨慎选择，GPU背后的intuition已经提了，而现代CPU内存也存在选择问题。当有内存分页机制（或者什么分段、段页）时，对于某块内存的取出是将其所在的页整个取出（如果我微机原理没记错的话）。如果所需的数据空间较为分散，频繁地调页将会浪费memory bandwidth：试想你为了SIM卡卡针去买了一部又一部的手机... 就为了里面赠送的卡针，顶级买椟还珠行为 --- 调一整页只为了其中的一小部分内容。此外，cache coherence也是一大考虑。频繁地更换在cache中的页将会导致大量cache miss，那就慢了啊。

​ 假设struct存储了某个个体中我们需要的信息，如果要追求极致速度，我们应该根据计算所需信息的内存分布选择SoA/AoS。举个例子：

  • struct中存储了位置，速度，加速度信息，我需要根据匀加速模型更新每一个个体的位置。一般来说，这种情况使用AoS比较好，因为计算使用的是struct的内部信息 --- 意味着我们需要struct的内部信息邻近性
  • 我的Flocking simulation：需要存储所有boids的角度、位置。例如当我希望邻近boids之间有相近的角度时，我需要访问其他boids的角度以及位置，此时使用SoA会比较好：利用同种类型的数据之间的邻近性，由于不同种类数据之间可能无法进行直接运算。

​ 我当时就没有把boid写成struct，而是进行了以下实现：

1
2
3
4
self.ang_vel 		= ti.field(ti.f32, self.boid_num)
self.angles 		= ti.field(ti.f32, self.boid_num)
self.pos 			= ti.Vector.field(2, ti.f32, self.boid_num)
self.dirs 			= ti.Vector.field(2, ti.f32, self.boid_num)

​ 角速度、角度、位置以及2D朝向（2D朝向用于结果绘制）都是分开存储的，虽然在计算角度时常常需要angles以及ang_vel，但其实这种不同类型的数据计算还是挺有独立性的。不过，AoS可能导致代码可读性变差（struct确实很有组织，正如我们存储人的身份信息时，一般都是把每个人作为一个单独的实例，内部有完整的各信息条目，而不会什么”年龄存一起，姓名分开并一起存在另外一个地方“）。

3.2 SSDS

​ 有四种node（四种SSDS支持的数据结构）：（1）Dynamic（本文不讲，原因见后）（2）Pointer：指针类型，每个区都可以指向完全没有空间规律性的地址（3）bitmasked：每个存储区存在一个1bit的flag，以指示当前存储区是否active（inactive的存储区将不会耗费除bit flag之外的内存）（4）dense：可以理解为field，无条件active的存储区，仅有dense的结构不是稀疏的。下面，给出官方教程的一个例子，关于具体的语法以及API的使用我就不说了，本博客也不是那种抄别人文档，代替读者paraphrase一下之后还给读者的那种答辩博客（虽然我博客内容质量也不行，但不至于开始就是答辩）。

1
2
3
4
5
6
7
8
9
x = ti.field(ti.i32)
y = ti.field(ti.i32)
z = ti.field(ti.i32)
S0 = ti.root
S1 = S0.pointer(ti.i, 4)
S2 = S1.dense(ti.i, 2)
S2.place(x, y) # S3: x; S4: y
S5 = S1.dense(ti.i, 2)
S5.place(z) # S6: z

​ 文档给出了存储结构图（注意，我觉得官方文档的图有问题，见下图的红框）。官方文档的红框区域中，靠上方的两个cell是2，下方两个为3，我感觉这是不对的，毕竟这违反了place的含义。

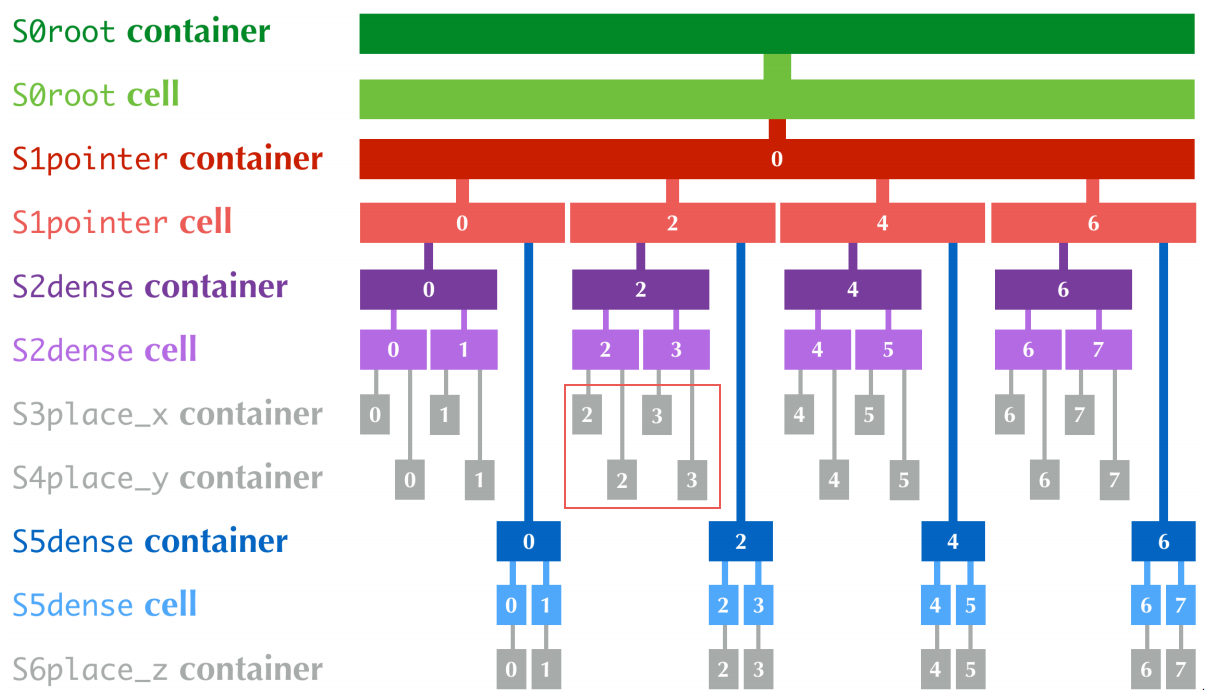
Figure 4. 层级结构图（灰色的container部分，被红框框住的区域为官方文档画错的区域）

​ 如果真想要深入学习Taichi，这张图的含义必须要完全看明白并且能与代码对上。按照图论中对树的理解开始即可，S0为根结点，根节点处有四个子树，每个子树都是一个pointer，所有子树归为S1层。S1层上每个子树上，挂两个子树，每个子树是一个dense存储区。对S2层而言，这一层是叶结点了，叶节点可以直接与某个field挂钩 --- 确定每个叶子元素是什么类型，在这里是i32。注意：x.place(y)函数可以理解为：将x所含有的层级结构，应用在变量y确定的存储区域上，存储区域的类型与y本身有关。下面我着重说一下flocking simulation中所需要的SSDS。

​ 我们知道（你知道吗），邻近搜索是一件很烦人的事情，特别是在元素较多的时候，因为对于人类来说邻近搜索简单直观：我要找出我附近的人并不要求我把我到所有中国境内的人的距离全部测一遍。而计算机比较暴力，简单地查找邻居需要基于距离度量。那用稀疏数据结构就是一种可行的加速手段，以搜索附近的人为例，我只要找出我当前所在县市周围县市人进行计算即可。Flocking simulation中我使用SSDS实现了稀疏grid（两层）：

  • 第一层，是2D pointer grid：代表了我对2D空间的划分 --- 划分为\((W/D) \times (H/D)\)个2Dgrid，每个grid大小为\(D\times D\)。那么对于一个boid，它只需要搜索自己所在的 + 邻近的（我代码内取8-邻域）grid即可
  • 第二层，1D bitmasked：由于我不知道会有多少只boid落在同一个grid中，所以我只能在开始时设置一个大的存储区（比如64 boids对应每个grid中需要有64个存储区）。使用dense显然... 不好，我可能根本用不到这么多存储区域，除非我代码写得有问题，鸟喜欢聚在同一个地方。bitmasked则是一个很好的选择，相当于有条件的dense结构

​ 第一层用pointer或者bitmasked都行，bitmasked是空间邻近的结构，pointer是离散存储的结构，在本用例中并没有太大的区别。用dense则不行：有些grid中可能一只boid都没有，没必要浪费这个内存。第二层的设计稍微有点tricky（可能是我想复杂了），理由如下：

  • boid在grid中的位置也是2D的，那么2D存储在1D的结构上自然要赋予一个地址值（或者下标索引）
  • Taichi喜欢lock-free操作（貌似在Taichi中也没有找到mutex）

​ 于是我的第一版实现是这样的：

1
2
3
4
self.mask_grids = ti.field(ti.u8)      # storing indices (atomic_add will return the original index, which is thread-safe)
self.sn_handle  = ti.root.pointer(ti.ij, (grid_x + 2, grid_y + 2))
self.atom_ptr   = ti.field(ti.u8, (grid_x, grid_y))     # atomic dynamic indices for bitmask (no offset needed)
self.sn_handle.bitmasked(ti.k, 128).place(self.mask_grids, offset = (-1, -1, 0))

​ mask_grids最终是\((W/D,H/D,C)\)大小的，其中C是每个grid能存储的boid数量上限，这个变量是我们用于邻近查找所需的变量。atom_ptr是一个原子操作数据，用于存储每个grid当前记录的boid数量。atom_ptr不仅有记录数量的能力，在并行计算时可以用于获取存储位置的数组下标：

1
2
3
id_x, id_y = int(new_pos[0] / self.radius), int(new_pos[1] / self.radius)
index = ti.atomic_add(self.atom_ptr[id_x, id_y], 0x01)
self.mask_grids[id_x, id_y, int(index)] = ti.u8(idx)          # store the index of the boid

​ 上面三行中，第一行先计算了grid坐标，此后ti.atomic_add将对应位置的计数+1，注意 其返回了+1之前的数组大小，可以直接当成我们的index使用。由于+1 / 返回原始值这个类似replace的操作是原子的，所以相当于我们可以进行lock free的动态大小存储。

​ 或许有人会说：为什么要这么复杂，我不能这样处理吗？既然是bitmasked，假设当前boid的id是k，那我只需要在masked_grid[i, j, k]处存储（或者activate）就可以了，根本不需要知道有多少boid、不需要atom_ptr以及原子操作啊？反正Taichi的 struct-for loop会自动遍历稀疏的active区域。

​ 不行！我们要实现的是手动for循环（三层），最外面的两层是在遍历当前grid以及其周围8-邻域grids，而最内层是在遍历存储在对应grid中的所有boid（记录的indices）。 struct-for loop 据我所知，不支持手动以及分步indexing（你写range限定范围是不行的，[i,j][k]这样的分步indexing方式也是不支持的）。

​ 此外，这里简单提一下与meta-programming有关的内容。Taichi的meta-programming貌似并没有C++/Rust那么复杂，并不涉及到非常底层的类型推断、泛型等问题。Taichi中的ti.template()与field作为函数参数输入有关，由于field是复杂的data container，其可以是scalar container，也可以是vector / matrix container，内部的类型也是可变的，作为matrix container时维度也是可变的。如果没有ti.template()而是要清楚地 type annotate 输入类型，会很繁琐，并且也不方便代码复用。使用ti.template()作为 type hint 可以方便输入不同类型的field。此外，如果需要达到 shape agnostic，可以使用grouped方法：

1
2
for I in ti.grouped(y):
    x[I] = y[I]

​ 可以避免：一维时x[i]，二维时x[i, j]，三维时x[i, j, k]这样与shape有关的写法。

​ 最后注意：

  • dynamic node在当今的1.3.0版本已经deprecated，所以不用特别关注。即将到来的1.4.0版本中，pointer以及bitmasked也将不再支持。我很好奇官方会推出什么替代方案。
  • @ti.pyfunc是已经deprecated的修饰符，虽然博文I中提到了，但我自己用了之后总是有warnings。
  • offset是很有用的功能，在field中，可以直接作为初始化参数设置offset，而对于SSDS，则在place阶段进行设置。offset可以实现padding，使得实现者无需考虑padding之后index的改变问题（这个学期写视频处理和宽带通信课的patch matching的时候老折磨了，padding之后的index得认真推）
  • 虽然我们只需SSDS最终的叶节点有想要的层级结构，适当地保存一些非叶节点作为handle，对于每次迭代需要清零的情况，可以使用handle直接执行：deactivate_all()方法以递归地deactivate当前以及所有子结点。

3.3 关于逻辑

​ 自己看代码吧，主要逻辑是这样的：

  • 角速度控制：直接控制的是角速度，角度更新根据角速度乘以系数。平滑随机方向：正常情况下boid的轨迹是随机的，但由于随机性体现在角速度上并且经过了很强的指数平滑，角度将会较为平滑地变化，轨迹是连续平滑的。有关随机性的实现，见基类boid_random_vel函数
  • 超界转向：参考oob_angular_acc，即超界后将会计算一个目标角度（当前位置到图像中心的方向角），随后使用P控制扭转方向
  • Alignment：搜索邻近boid，根据距离加权角度（由于角度加权存在奇异性问题，故加权方向向量后atan2函数转为角度）
  • Separation & Cohesion：两者实现在一起，都需要计算当前位置到局部质心的方向向量。Separation倾向于原理局部质心，而cohesion倾向于靠近局部质心。接近与远离依靠目标角的方向实现：接近即目标角指向局部质心，远离即目标角指向局部质心方向旋转180°后的结果。当前应当接近、远离按当前位置距离质心的距离确定，参考粒子间作用力模型，实现是一个不对称截断（clamp）的平移后tanh函数。
  • 普通鸟与掠食者（普通鸟就是鸽子，Pigeon类），掠食者之间不会相互作用或者配合。普通鸟存在警戒范围，倾向于远离警戒范围内的掠食者（的质心），而掠食者将在掠食范围内追踪距离最近的普通鸟。
  • 掠食者可以进行自动控制，也可以选其一进行鼠标控制（跟踪鼠标方向）

IV. 传统艺能-结果

​ 结果如下，45FPS的样子（注意，如果使用arch = ti.gpu，需要把代码中的atom_ptr类型从u8换为i32，貌似GPU不支持u8 atomic_add，我记得也是这样，有些数据类型，有符号的原子操作存在，无符号则不存在）。

Figure 5. 什么鸟视频

​ 如果你感兴趣，安装Taichi之后可以自己clone我的 learn_taichi 库，在learning_examples中，flocking_sim.py可以直接运行。参数在if __name__ == "__main__"后。如果需要开启鼠标控制其中一只掠食者，请将line 262的last_one_human改为True。注意，当前代码暂不支持无掠食者（在我前几个commit中应该是有无掠食者的，现在的代码稍微有点复杂）。

​ 最后提一句，如有有兴趣，看官方文档，官方文档质量非常高。看完就自己写写，文档不是看会的，是用会的。

Reference

[1] In CUDA, what is memory coalescing, and how is it achieved?

[2] Taichi Lang Docs v1.3.0: Spatially Sparse Data Structures