AdaPT - Monte Carlo Path Tracer I
Ada Path Tracer I
Path tracing背后的概率与数学理论较为复杂,如果不深入理解则很难进行正确的实现,更勿论在此基础上进行创新了。结合笔者在实现过程中的一些体会,笔者认为非Whitted光线追踪渲染器有一个这样的特点:即使是很大的逻辑错误可能也很难使用定性的方法观察出来,最后的错误输出可能与正确输出仅有很小的差别,甚至有的时候根本看不出来(例如,算法收敛慢时我可能倾向于认为是自己没有用太多的variance reduction方法以及深入的采样技术,而不会认为我代码有逻辑错误)。故本文作为 Path Tracing 系列的第一部分文章,将尽可能深入讨论背后的理论知识以及其理解。理解是为实现、创新服务的,任何不到位的地方都将导致实现过程中的卡顿,故此处我将尽力覆盖这两周用零碎事件写渲染器: AdaPT时所遇到的问题。
写文档是很烦人的一件事,如果我本身很闲,不用为了各种学业、科研、个人资本等等事情考虑的话,我当然还是非常愿意写博客、写文档的。可惜写博客写文档从现在来看并没有实际的价值,只是我个人的自嗨。 --- 2023.2.8 何千越
| "The cornell spheres" | "The cornell boxes" |
|---|---|
 |
 |
II. 基本概念与基本应用
2.1 Monte Carlo积分
一般来说,积分要比求导困难一些。这是因为很多函数(作为导数)的原函数很难,而与导数不同的是,数值导数可能往往只需要两个值就能近似,积分则可能需要巨量值,尤其 是在高维空间中(多重积分)。
考虑到随机算法有时可以加速某些迭代类算法的收敛,在积分计算问题上,我们也可以尝试使用随机算法。下面引出问题:设待估计函数 \(f(x)\) 在区间 \([a, b]\)上的积分为: \[ I = \int_a^b f(x) dx \] 设有一随机估计器\(\hat{I}\),此估计器用于估计\(I\),则\(\hat {I}\) 应当是无偏估计。并且我们希望 \(\hat{I}\) 是最有效的估计,也即多次估计的方差最小(这个问题将在第三章讨论)。不难看出,如下估计子是无偏的: \[ \hat{I}=\frac{1}{N}\sum_{i=1}^N\frac{f(X_i)}{p(X_i)} \] 根据如下推导可以非常轻易地获知,注意\(f(X_i)\) 是随机变量,\(p(X_i)\)为随机变量\(X_i\)取值一定时的PDF。 \[ \begin{align} E(\hat{I}) &= E\left( \frac{1}{N}\sum_{i=1}^N\frac{f(X_i)}{p(X_i)} \right)=\frac{1}{N}\sum_{i=1}^N E\left(\frac{f(X_i)}{p(X_i)} \right)\\ &=\frac{1}{N}\sum^N \int_\Omega \frac{f(x)}{p(x)}p(x)dx = \frac{1}{N}\sum^N \int f(x)dx = \int f(x) dx \label{der1} \end{align} \] 虽然,除以PDF这种事情... 并不是一眼就能知道其背后的数学直觉的。关于数学直觉,外网有很多解释Monte Carlo积分的文章,这里只讲一种最简单的入门级理解方法:假设\(f(X_i)\)在\([a, b]\)上均匀分布,那么PDF就成了\((b-a)^{-1}\),除以\(p(x)\)则成了乘以\((b - a)\)。则每个样本相当于计算\(f(x) \times (b - a)\)(某个矩形的面积),进行多次面积估计并平均则可以得到结果。如果把均匀分布换为其他任意分布也有一样的结果。Monte Carlo积分非常有用,它使得我们可以处理难以进行积分的函数。
2.2 在光线追踪中的应用
难以积分的函数?举个例子,空间中某一点的 Radiance 计算公式: \[ \begin{equation}\label{radiance} L_o(x, w_o) = L_e(x, w_o) + \int_\Omega L_i(x, w_i) f_r(w_i, w_o, x) \cos\theta dw_i \end{equation} \] 其中\(w_i\)为入射光方向,\(w_o\)为出射方向,\(x, n\)分别为光线击中点与击中点法向量。\(\cos(a, b)\)代表了两个向量之间的夹角余弦值(也即归一化后的内积),\(L_{e}\)则为击中点为\(x\),入射方向为\(w_i\)的 radiance。上式是将各个入射方向的光进行积分:先按cosine规则进行衰减,后按照BSDF进行“入射到出射的mapping”加权积分。公式\(\eqref{radiance}\)右边的“各方向入射irradiance”部分是很难衡量的:多光源,多次反射,遮挡(包括shadowing以及masking),解析解绝对不要想。则我们可以考虑使用Monte Carlo积分,把积分换为: \[ \begin{equation}\label{discrete} \frac{1}{N}\sum_{j=1}^N \frac{L_{i,j}(x, w_{i,j}) f_r(w_{i,j}, w_o, x) \cos\theta}{p(?)} \end{equation} \] 如果,我们可以设法计算\(L_{i, j}, f_{r}\) 以及 \(p(?)\),一切将变得“轻松”。好,那么 p(?) 究竟是什么?我应该求解什么的分布?是\(w_i\),还是\(L_{i,j}(x, w_{i,j}) f_r(w_{i,j})\) 还是整个分子项?(注意\(\cos\theta\)也是\(w_i\)的函数,因为\(\theta\)是 \(w_i\) 与法向量 \(n\) 的夹角),三种情况的分布是不同的 --- 随机变量函数的分布不一定等于原分布。从公式\(\eqref{der1}\)可以知道:\(p(x)\)应当是\(f(x)\)的分布,才能得到无偏的估计。此处的 \(f(x)\) 显然是整个分子项。下面,我来重点讨论一下分子的联合分布(学了点随机过程还是... 有点作用的,虽然忘得差不多了)。
分子项将需要被 分解 为两部分:
- 直接光照(direct component):采样光源与一次反射
- 间接光照(indirect component):采样光线弹射方向,使得光继续在空间中传播
拆分之后,两部分的PDF计算是不一样的。一定要注意,分子项的三部分\(L_i, f_r, \cos \theta\)并非全都是随机变量,并非全都会有附属的分布(PDF)。直接光照中,$f_r, \(不是随机变量,不需计算其分布;间接光照中由于\)L_i$并非即刻计算(需要后续弹射计算),故不计算此分布。分解思想我将在2.3节中详细介绍。
我现在的渲染器(截至2023.2.7)也才只写到透明折射物体(非散射)部分,等到散射部分加入后,radiative transfer equation(RTE)将会更加复杂。在更加复杂的函数作为被积函数
2.3 分解法与分布变换 - 从理解到实现
2.3.1 直觉理解
从公式\(\eqref{discrete}\)来看,光线追踪似乎是一个指数爆炸式的递归过程:光线在每一个击中点都发出N条光线,那么弹射\(n\)次意味着\(N^n\)条光线。但我们可以将其简化:只trace一条光线。这种方案被称为:path tracing。注意,此处我们考虑的是单向(unidirectional)path tracing,并且方向是从 相机(sensor)到光源。
回到2.2中的问题:直接光照与间接光照的分解问题。直接光照为光源发出的光仅经过一次弹射就到达sensor的部分,间接光照则需要更多次弹射。但,对于整条路径:\(v_s, v_1, v_2, ..., v_n\) 而言(\(v_s\)为传感器,\(v_n\)为第n次光线与场景相交),在某一处的\(v_j\)的直接光照将变为在某一处\(v_i (i<j)\)处的间接光照:
graph RL A(...)-->|indirect from v...|B(v3)-->|indirect from v3|C(v2)-->|indirect from v2|D(v1)-->E(sensor) F(direct v1)-->D G(direct v2)-->C H(direct v3)-->B
故事实上,我们没有必要直接去讨论间接光照,间接光照 就是此节点后节点上的直接光照。故我们只需要讨论:
每一个节点处的直接光照。如何计算?采用Monte Carlo积分(下式将与距离衰减,光源出射衰减项整合到了\(L\)中):
\[ \begin{equation} L_d(x, w_o) = \frac 1N \sum_{i=1}^N \frac{f_r(x, x_{l, i}\rightarrow x, w_o) L(x_{l, i},x_{l, i}\rightarrow x )\cos (x_{l, i}\rightarrow x, n_l)} {p(x_{l, i})} \end{equation} \] 最理想的情况当然是进行积分:对每一个光源,光源上的每一个点(假设是有面积光源)\(x_l\),计算此点照射在\(x\)点(当前vertex)处的irradiance(与cosine项相乘),结果乘以BRDF(BxDF,可能是别的函数)转为输出光。实现时则在所有光源上取共N个点(shadow rays),计算每个采样点的分布\(p(x_{l, i})\)以及上式中其他部分,最后平均。
光线需要传输,间接光照的radiance是传过来的。假设我们有一条光路击中\(v_j\),也即\(v_{j-1}\rightarrow v_j\),则接下来需要知道三件事:
- 新的传输方向计算: 什么样的光击中\(v_{j}\)点后有很大概率可以传输到\(v_{j-1}\)?注意,在backward tracing中,我们从相机开始trace rays,方向是\(v_{j-1}\rightarrow v_j\),但实际情况是:光源(位于\(v_{j+1}\))发射光击中\(v_j\),\(v_j\) 处产生材质/介质 interaction后将光源的光反射到 \(v_{j-1}\) 处。故我们需要知道的实际是:\(v_{j + 1}\)可能在什么位置?也即,如果已知\(v_{j-1}\rightarrow v_j\),我们需要知道\(v_{j+1}\)在什么位置才能使得由此点发出的间接光照可以通过 \(v_{j+1}\rightarrow v_{j }\rightarrow v_{j-1}\) 传输?假设我们考虑\(v_{j}\)位于完美的镜面上,则根据一般的光路可逆原理,\(v_{j+1}\rightarrow v_j\) 一定在 \(v_{j-1}\rightarrow v_j\) 的反射方向上。更加一般的情况则需要视BSDF而定。
- \(v_{j+1}\rightarrow v_j\) 的“可能性”(PDF值):还是以镜面为例,我们必然会在反射方向附近(假设镜面不是完美的)采样新的光线方向。每个方向都有其可能性值(PDF),例如当光线垂直镜面入射时,在平行镜面方向的可能性几乎为0。
- 传输率计算: 我们的光线追踪器不可能只考虑完美镜面。故 \(v_{j+1}\rightarrow v_{j}\) 传输的radiance将很可能在 \(v_j\) 处根据BSDF进行衰减,衰减后的值成为 \(v_{j}\rightarrow v_{j-1}\) 上传输的radiance。 传输率会被称为:throughput,在我的代码里,则称为 contribution。
有了以上两个部分:(1)直接光照(2)间接传播的方向、PDF以及传输率,我们就可以类似图2这样,逐层递归分解光。所以,我可以说:最后到达相机的光,是【击中光源的光\(L_e\)】以及每一个节点上、可能经过多次弹射的【直接光照】。(注意,BunnyKiller(Jarabo 2014)中并没有计算\(L_e\),所以它看不到面光源的样子... 代码中也有很多错)
注意,在面光源情况下,我们不trace shadow rays(不计算积分部分),只计算\(L_e\)(击中光源后部分)也是可以完成正确渲染的,但是,收敛会慢很多很多。笔者之前的代码中有个bug,shadow rays全是错的,direct component全部为0,也得到了对的结果,但收敛一直很慢,MIS加上了也很慢;之后才发现 direct component 根本没有算,修改后简直就是“光速收敛”。故这也印证了我在 introduction 中所讲的:即使代码错了,结果也可能对(或者错误肉眼看不出来)。这就是此类渲染器 debug 的困难之处。
2.3.2 计算过程
废话了很多,现在我来讨论一下两部分的计算。这里我们举两个非常常见的例子:点光源与面光源,并且我们假设场景中最多有两个光源(不失一般性)。则某一处的出射光线可以被分解为直接与间接光照(不考虑自发光): \[ \begin{equation} L_o(x, w_o) = \int_\Omega L_{in}(x, w_i) f_r(w_i, w_o, x) \cos\theta dw_i + \sum_{i=1}^M\int_A f_r(x, x_{l, i}\rightarrow x, w_o)L(x, x_{l, i}\rightarrow x)\cos\theta dA(x_{l, i}) \end{equation} \] 第一部分:间接光照,第二部分:M个光源上每一点在\(x\)处的直接光照,\(L_{in}\)包含了\(G\): \[ G(x_{l, i}\leftrightarrow x) = V(x_{l, i}\leftrightarrow x)\frac{|\cos(w_i, n)(\cos{(w_{i}, n_e)})|}{\Vert x_{l, i} -x\Vert ^2} \] 其中:
- \(V(·)\)项就是visibility项,需要光源与击中点之间没有遮挡物,此项一般无需采样(直接判断)。
- cosine term的第一项很熟悉了,光源入射面的cosine衰减。
- 第二项为\(\cos(w_{i}, n_e)\),其中\(n_{e}\)为光源出射位置的法向量(例如面光源的面法相)。这项看起来有点奇怪,实际上与一种叫做“projected solid angle”有关,解释见下引用块以及一张图。由于光源输出光按照立体角定义(radiance与irradiance),光源radiance若本身含有cosine项,可以将此项移动到立体角部分。
Projected solid angle has meaning primarily for a small Lambertian source, which has intensity that varies as the cosine of the angle with the surface normal [1]
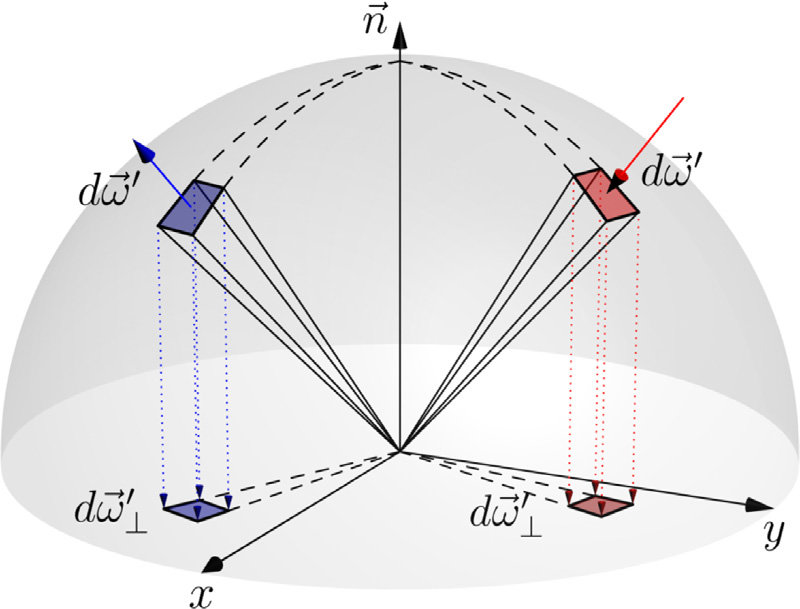
写成代码可实现的离散情况(用Monte Carlo积分表示): \[ \begin{align} L_o(x, w_o) = \frac 1N \sum_{j=1}^N \frac{L_{in}(x, w_{i, j}) f_r(w_{i, j}, w_o, x) \cos\theta}{p(w_{i, j})} + \notag \\ \frac{1}{N_s}\sum_{j=1}^{N_s}\frac{L_{l, j}(x, x_{l, j}\rightarrow x) f_r{(x, x_{l, j}\rightarrow x, w_o)}\cos\theta}{p(x_{l, j}|e_j)p(e_j)} \end{align} \]
2.3.2.1 直接光照的计算
(1)首先采样光源,比如:两个点光源选一个。一般来说我们用等概率选择不同光源(面光源可能需要根据面积进行加权)。此处会返回一个PDF:选光源总有概率吧,例如两个光源时一般用\(0.5\),记为\(p(e_i)\)
(2)在采样后的光源上进行点采样:点光源不用采样(只有一个点嘛),面光源则根据实现不同有所变化。例如在我的代码中,我的面光源是可以attach到某个物体上的(比如发光的墙、盒子、球等等),物体表征如果为mesh,则需要首先采样面片,此后再在面片上采样点,而如果是显式几何表征(比如一个矩形),则为面积的倒数(均匀分布假设)。记此概率为
\(p(x_l|e_i)\),注意此概率为给定光源之后的条件概率。
(3)要用什么概率计算?角度积分与面积积分是完全不同的。如果仅仅是在面光源上采样,当然可直接使用\(p(x_l|e_i)p(e_i)\)计算PDF,但 如果要进行MIS(mutiple importance sampling),就必须将光源采样与BSDF采样转化到同一个空间下讨论。这个部分我们留到第三章说。
(4)多光源或者是大型面光源时,尽量多使用一些shadow rays,有助于收敛。
以上技术就是著名的:”Next Event Estimation“
Idea: follow each ray via multiple indirect bounces, but at each bounce, compute the direct lighting from light source surfaces!
- Detected light at each bounce is no longer dependent on coincidence
- This is what we refer to as Next Event Estimation
2.3.2.2 间接弹射的计算
(1)根据来自sensor方向的入射光线、法向量以及BSDF,采样出射方向(backward tracing意义上的出射,实际我们在确定物理意义上的入射,这点需要清楚理解!)。
(2)既然是采样,我们可以在采样过程中算出对应的PDF。注意,采样的PDF值应当是\(f_r(x, w_i, w_o)\cos\theta\) 的PDF值(但采样所用的分布可以是任意的,但越像\(f_r(x, w_i, w_o)\cos\theta\) 越好,但这个内容与Importance sampling有关,本篇博客就不细讲了),而不是简单地与\(f_r(x, w_i, w_o)\)有关。为什么呢?我们实际想采样的是\(w_o\) (我们需要一个出射方向),但是与出射方向有关的函数则是\(f_r\) 以及 \(\cos\theta\) (由于只讨论传输率,故没有\(L_i\)这一项)。
(3)计算传输率。此处注意,\(\cos\theta\) 是出射方向与法线之间的夹角(多次说过,backward tracing的出射是物理意义上的光源入射)。
(4)注意!不管实现什么BRDF/BSDF,一定要使得结果满足能量守恒:传播过程不会导致能量越来越大。
2.3.2.3 能量守恒
开始时我的代码不满足能量守恒,传播会导致 radiance 越来越大(最后画面全白,出现inf/NaN)。刚开始时我还非常疑惑:除以PDF时,如果有非常小的PDF,难道不会将radiance放得很大吗?但事实上这样的担心并不存在,由于 BSDF 有放缩系数。我开始认为:BSDF应当是一个相对值函数:最大反射/透过率的位置的值为1,其余位置小于1。但实际上 BSDF 需要归一化,关于归一化,这里有两个非常好的回答(与博客)[4] [5]。
有关Lambert's Cosine Law的问题,这里我也简单说一下(由于这个问题当时也困扰了我很久)。首先,是半球积分的概念。我们在讨论时常常使用\(w_i/w_o\)来代替方向。而对应的 \(dw\) 则是 对应某个方向\(w\)的微分立体角(differential solid angle)。立体角!并不是一个很好讨论的玩意,你说如何用它进行积分?我也不知道,我们需要将其展开为熟悉的多重积分(在笛卡尔坐标系下或者球坐标系下)。注意微分立体角与球坐标系(\(\theta\) 为zenith angle,或者说是elevation angle,\(\phi\) 是 azimuth angle)之间的转换: \[ \begin{equation} dw = \sin\theta d\theta d\phi \end{equation} \]
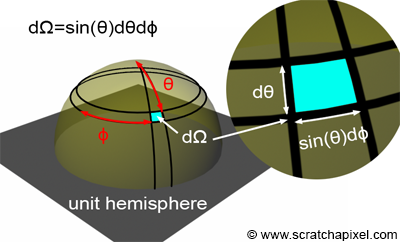
注意范围,俯仰角\(\theta\in[0, \pi/2]\), 方位角\(\phi \in [0, 2\pi)\)。此 \(\sin\) 项的存在解释了normalization factor计算中,直接用 \(d\theta d\phi\) 算出的结果不对的原因。
而BSDF的能量守恒则可以这么定义: \[ \begin{equation}\label{bsdf_norm} \int_\Omega f_r(x, w_i, w_o)\cos\theta d w_i\leq 1 \end{equation} \] 此外,个人认为还有一种定义方法: \[ \begin{equation}\label{nq} \int_\Omega L_o(x, w_o) d w_o\leq \int_\Omega L_i(x, w_i) d w_i \end{equation} \] 这个给出一个 Lambertian 表面的例子:
A surface with a Lambertian BRDF has the characteristic that independent of the direction from which one looks at that surface, one receives the same amount of reflected energy (i.e. a diffuse surface point looks the same from all possible directions) [4]
[4]处的思想见下图。下图可以表示两种情况:
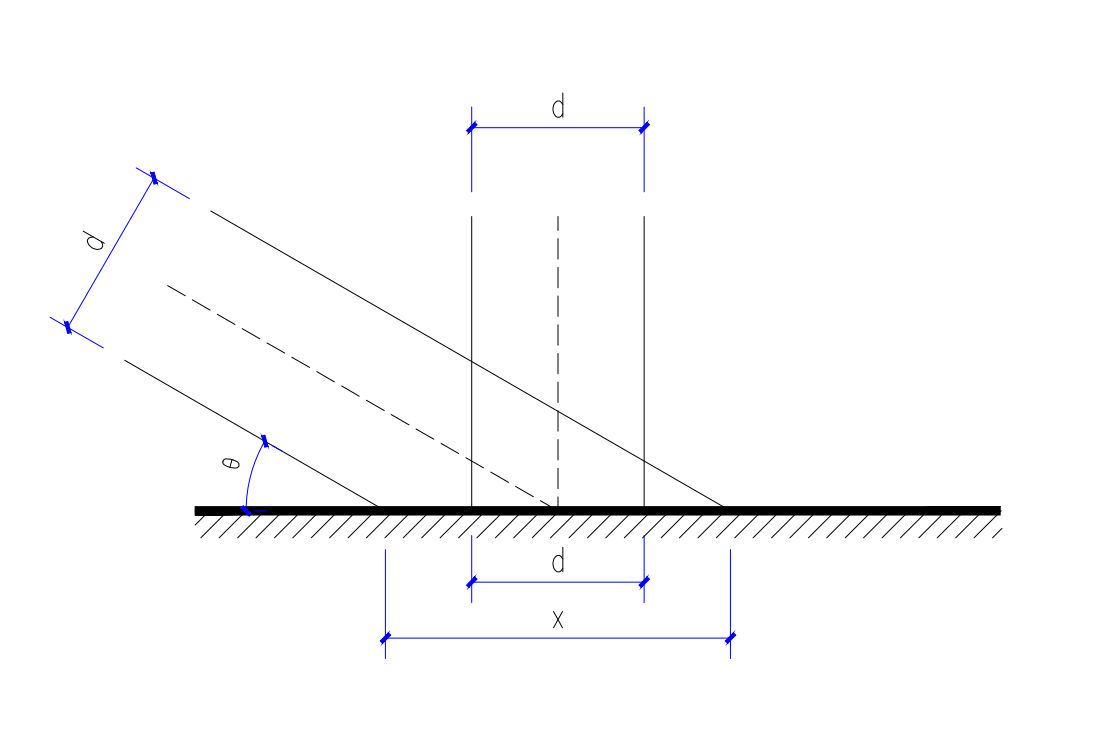
- 等直径光柱以不同角度入射一平面:可知角度越大,单位微元内入射光强度越小。这就是 Lambert's Cosine Law 的由来。也是path tracing算法中每一项BSDF(除了 delta 类 BSDF,如镜面)都需要乘的 cosine 项
- 某一像素的视角范围。为了简单起见,像素的 FOV 原本为锥形,在距离较远时直接简化为等宽的柱体。可知,入射角度越大,截面积越大(对应的 radiance 自然就更多?)。但实际上我们求 radiance 时是在柱内求平均而非求和(或者面积积分),故这种解读实际上并不影响结果(事实上,我所知道的renderer中貌似都没有除以\(\cos\theta_i\)的操作)
我们结合 Lambertian 表面的定义:各方向观察同一点,radiance 应当一致。则可以得到: \[ \begin{align}\label{lambert} &\int_\Omega \cos\theta \rho_d d w_o \\ &=\rho_d\int_\Omega \cos\theta d w_o \\ &=\rho_d\int_0^{2\pi} \int_0^{\pi/2} \sin\theta \cos\theta d\theta d\phi \\ &=\rho_d\pi \end{align} \] 故由于上式需要小于等于1,则Lambertian对应的 normalization factor 是 \(\pi\)(对应\(\frac{\rho_d}{\pi}\pi=\rho_d\)),对应其BSDF为 \(\rho_d / \pi\)(也即是均匀的)。
Todo
最有趣的(也是比较恶心的部分),当属采样以及进行BSDF的设计。如何设计正确的BSDF --- 正确归一化的BSDF函数,高效率的采样以及正确的PDF是我们需要关注的重点问题(也是当前我对算法理解的最大障碍,估计也是后续工作需要重点掌握的基础知识)。举个例子:Lambertian PDF 为什么是 \(\cos\theta /\pi\)?以及其 cosine weighted 采样为什么要这样设计?很惭愧,脑子不好使,确实一时半会儿答不出来。故这部分将成为下一篇博客的重点。
References
[1] AdaPT-Monte-Carlo-Path-Tracer-I
[2] Bernhard Kerbl - Rendering: Next Event Estimation
[3] Wang, Zhen, et al. "Theoretical extension of universal forward and backward Monte Carlo radiative transfer modeling for passive and active polarization observation simulations." Journal of Quantitative Spectroscopy and Radiative Transfer 235 (2019): 81-94.