AdaPT - Volumetric Path Tracer I

Posted on 2023-02-18 In learning Views: Symbols count in article: 13k Reading time ≈ 12 mins.

Ada Path Tracer III

AdaPT 进入了 volumetric path tracing 阶段。由于本人的研究方向（暂定）为散射介质渲染的研究，了解基于 particles 的（Lagrangian表征的）散射渲染是非常有必要的（烟雾渲染多有意思，虽然现在只能渲染 homogeneous 介质）。vpt相对于无介质pt的主要难点在于：

volumetric path tracing 在采样层面上多了一个维度 --- 光线传播距离将不再是无穷远，需要采样其自由程
free space radiance 一致性不再成立，并且模型与表面散射模型有较大的区别。有许多额外计算需要完成
direct component 更难衡量，这意味着收敛更加困难。MIS 也不那么 intuitive 了

渲染4000迭代（25s，约10亿光线）	渲染20000迭代（约50亿条光线）	渲染15000迭代

Figure 1. 无介质的收敛性明显好很多

话说，我写博客从来没有在一个系列上写超过两篇的文章，渲染技术系列已经三篇了，这还是头一回。

2.1 基本概念

2.1.1 Abosorption

吸收与\(\sigma_a\): 吸收系数（absorption cross section），是一个PDF：probability density that light is absorbed per unit distance traveled in the medium

The units of are reciprocal distance (\(m^{-1}\)). This means that can take on any positive value; it is not required to be between 0 and 1, for instance.

吸收系数的单位之所以是\(m^{-1}\)，是因为如下关系： \[ \begin{equation}\label{absorb} L_o(x, w) -L_i(x, w)=-\sigma_a(x, w)L_i(x, w)dt \end{equation} \] 其中，\(dt\)是微分距离（光线通过一小段散射介质），\(L_i(x, w)\)为位置x，入射方向为\(w\)的入射光radiance。在各向同性介质假设下，可以通过求解微分方程的方式算出： \[ \begin{equation}\label{remain} L_o(x+w\cdot t, w) = L_i(x, w)e^{-\int^{t}_0 \sigma_a(x + w\cdot \tau)d\tau} \end{equation} \] 以上公式就是著名的 Beer-Lambert 定理。

2.1.2 Emission

emission：emission... 我本人挺少接触这个概念，可以认为是medium本身的一种“荧光反应”？这种现象对 output radiance 的影响公式为： \[ \begin{equation}\label{emission} dL_o(x, w) = L_e(x, w)dt \end{equation} \] 关于这个公式，我在PBR book中读到这样一段话：

This equation incorporates the assumption that the emitted light \(L_e\) is not dependent on the incoming light \(L_i\). This is always true under the linear optics assumptions that pbrt is based on.

我对以上公式倒是没有什么感兴趣，只是觉得这里的 linear optics 有点奇怪。emmm 什么是 linear optics assumption? 我在研一上学期的【生物医学光学】课程中曾经学到【非线性光学】的概念，我印象最深的非线性光学概念就是拉曼散射（但显然不可能出现在图形学的渲染问题中，拉曼散射比普通散射的强度低好几个数量级）。如果与某些非线性光学效应有关，我就还有很多光学知识需要补... 个人觉得可能存在这样的一种情况：我曾经读到过光致透明/光致变色的有关内容，假设 emission 与入射光有关，那么 \(L_e(x, w)\) 将会比较复杂，是入射 \(L_i(x, w)\) 的函数，建模起来就需要一些数学手段。

2.1.3 Out-scattering

out-scattering: 光线偏离原本方向，向别的方向传播而损失能量的过程。out-scattering 也是线性微分方程建模（这可能就是缺陷所在）： \[ \begin{equation}\label{out-scat} dL_o(x, w) = -\sigma_s L_i(x, w) dt \end{equation} \] 显然，我们可以把公式\(\eqref{absorb}\)与公式\(\eqref{out-scat}\)组合在一起，得到系数 \(\sigma_t = \sigma_a + \sigma_s\)，称之为 attenuation 或者更为熟知的【extinction】。\(\sigma_t\) 是个重要概念，由它定义了两个概念:

Albedo: \(\rho = \sigma_s / \sigma_t\)，从公式看也即散射相对于两种 interaction 事件发生的比例。也即发生散射事件时，散射（而非吸收）的概率
平均自由程：\(1/\sigma_t\)。都是伏笔，还记得\(\sigma_t\)的单位是\(m^{-1}\)吗... 倒数的单位就是\(m\)了：光线发生一次散射事件前行进的平均距离。

emmm，有了\(\sigma_t\)以及公式\(\eqref{absorb}\)与\(\eqref{out-scat}\)，我们可以定义一个新的 "Beer-Lambert" 公式： \[ \begin{equation}\label{remain2} L_o(x+w\cdot t, w) = L_i(x, w)e^{-\int^{t}_0 \sigma_t(x + w\cdot \tau)d\tau} \end{equation} \] 以上公式计算的结果中，指数项被称为 transmittance（传输率），由于指数项的存在（linear optics），传输率是可乘的（乘等于通过两端路径之和）。exp的指数项被称为光学厚度（optical thickness）: \[ \begin{equation}\label{opt-th} \tau(x\rightarrow x') = \int_0^t\sigma_t (x+tw, w)dt \end{equation} \]

This property is useful for volume scattering implementations, since it makes it possible to incrementally compute transmittance at multiple points along a ray.

这也同样需要注意，我同样希望拓展的模型也具有此性质，这样的系统将会是无记忆系统，容易实现并且对并行计算是友好的。【无记忆性】

2.1.4 In-scattering

in-scattering 需要引入相函数（phase function）概念，此概念与BSDF很像，我们可以认为BSDF是表面的相函数，BRDF则一般定义背向散射，BSDF则同时定义前向与背向散射。

PBR-book 给出了 BSDF与phase function的一个重要不同，回顾BSDF的性质：BSDF具有“归一性质”： \[ \begin{align}\label{norm1} \int_{\Omega} L_i(x, w_o)f_r(x, w_i, w_o)\cos\theta dw_o &\leq L_i(x, w_i)\\ \int_{\Omega} f_r(x, w_i, w_o)\cos\theta dw_o &\leq 1 \end{align} \] 但由于 medium interaction 并没有 cosine's law，并且 phase function并不建模能量衰减，故 phase function 是直接、完全归一化的： \[ \begin{equation}\label{norm2} \int_{S^2}p(w_i, w_o)dw_o = 1 \end{equation} \]

The main difference is that there is no cosine term since the phase function operates on radiance rather than differential irradiance.

phase function 实际上就是散射方向的PDF。关于 phase function，这里只提一点：大多数phase function都可以用 H-G phase function 的线性组合近似[1]。

2.2 Radiative Transfer Equation

definitionThe light transport equation is in fact a special case of the equation of transfer, simplified by the lack of participating media and specialized for scattering from surfaces. [2]

很重要，就推导两对效应：

absrption / out-scattering (radiance 减少)
emission / in-scattering (radiance 增多)

带来的影响，以及从 surface 入射的 radiance 如何对当前一点的入射 radiance 起作用。首先，这里展示无介质情况下的 light transport equation： \[ \begin{equation}\label{lte} L_o(x, w_o) = L_e(x_h, w_o) + \int_\Omega f(x_h, w_i, w_o)L_i(x_h, w_i)\cos\theta dw_i \end{equation} \] 其中，\(x_h\)为\(x\) 沿着\(-w_o\) 方向交场景的最近交点（first intersection）。此 LTE 我们很熟悉，也即emission与击中点半球上入射光反射的积分和为出射光，上一篇博客我们也分析了此公式的分解实现。但上述公式中，我们并不清楚场景的几何配置、可视信息等，而这些信息实际上在上述公式中又至关重要。例如在分析直接光照时：

如果是无介质直接光照，需要trace shadow ray并且确认 shadow ray 并没有【除了被采样光源之外的其他几何体】遮挡。
如果是有介质直接光照，需要进行多次 tracing：由于对应的几何可能是 null-surface (用于限制medium的假想surface)，直到 tracing 到达non-null surface 或者光源后就停止。

在开始介绍 radiative transfer equation 之前，我想提一下 Geometry term 这个东西。

2.2.1 Geometry Term

建议先了解一下这个知识：The Integral With Respect to a Measure（其中nelv的回答。关于某种度量的积分，这里的measure说的并不是概率测度）。

Think of it physically: each measure assigns different weights to given sets: consider for example the particular case \(dμ=df(x)=f'(x)dx\) for a well behaved f(x). Here you can really see the difference between the "ordinary" measure \(dx\), which does not care about the location of the set, and \(f′(x)dx\), which indeed does!

也即：我们关心的微元，究竟表达了什么实际意义？nelv举的例子：对于普通 \(dx\) 度量的积分问题来说： \[ \begin{equation} \int_0^1dx = \int_1^2dx = 1 \end{equation} \] 而如果我们的度量不是 \(dx\)，而是 \(df(x)\)，则显然，上述积分的结果会变成：\(f(1) - f(0)\)以及 \(f(2) - f(1)\)，两者是否相等取决于函数性质。将“度量”不同导致“积分形式”不同的想法迁移到 path tracing中，我们不难找到如下的例子：

投影固体角（projected solid angle）
irradiance积分

上篇还是上上篇已经说过了。投影固体角是为了处理 \(\cos\theta\) 项的一种表征。由于在 irradiance 积分中，有： \[ \begin{equation} \int_\Omega f(x_h, w_i, w_o)L_i(x_h, w_i)\cos\theta dw_i \end{equation} \] 上述 \(\cos\theta\) 可以被消去，如果将立体角变为投影立体角。简单理解就是：由于立体角实际上是某个物体【张成的3D角度】在【单位球上的投影面积】（对应2D中某线段确定的弧长），那么这个面积可以投影到单位球中由物体表面法向量确定的圆盘上（由3D面积投影为2D面积），也即： \[ \begin{equation} d w_i^{\perp} = \cos\theta dw_i \end{equation} \] 这就是一种不同的度量，面积微元由投影微分立体角决定。积分空间也会对应改变为2D圆盘而非3D半球。

一种更加复杂的情况，虽然这种情况之前已经多次讲过（BSDF/emitter采样）。观察公式 \(\eqref{lte}\) 中的 irradiance 积分，不难发现积分空间是法向量确定的半球，度量是微分立体角。我们可以将其转换为另一种度量：对某一个面光源而言，面光源上每一点对空间中某一点的 irradiance 贡献。此处：对面光源上点进行积分使用的是【面积微元】，积分空间为【光源表面】（对应emitter sampling），而公式 \(\eqref{lte}\)中的 irradiance积分，其度量已经讲过（对应了BSDF sampling）。两个度量之间存在转化关系，转化关系的示意图见上一篇博客的Figure.3。

度量之间的转化关系非常重要，贯穿于 path tracing 的 importance sampling，上次读论文时看到这么一句话：

Converting from the solid angle×length product measure to the volume measure requires multiplication by a corresponding geometry term G. [4]

也即，Geometry term 可以用作度量转换。在 PBR-book [3] 中，有非常详细的 geometry term 用于度量转换的例子 14.4.3 The Surface Form of the LTE，这里就不浪费笔墨去拾人牙慧了。这也解答了我之前在 stackexchange.cg 上提问的一个疑惑（我自己写了回答）：为什么 \(L_e\) (emission项) 并不需要 distance attenuation 或者 \(\cos\) term？因为 emission evaluation 使用的度量是立体角而非面积微元。\(L_e\) 本身返回的就是某个方向的 radiance (radiance 在非 volume path tracing 情况下，在两个表面点之间是不变的)。

在 geometry term 讨论的末尾，我想顺带写一下我对最近读的一篇好文章 [4]ACM ToG 2013 中某些点的理解。以其论文中的公式 \((4)\) 以及对应的 equiangular-sampling 方法为例子（我还没学到 bidirectional path tracing，所以这部分的理解可能会有误） \[ \begin{equation}\label{equi} p(t_{dc} | b, d, w_{dc})\propto G(b, c) = 1/\Vert b - c\Vert^2 \end{equation} \]

Figure 2. Equi-angular sampling 方法

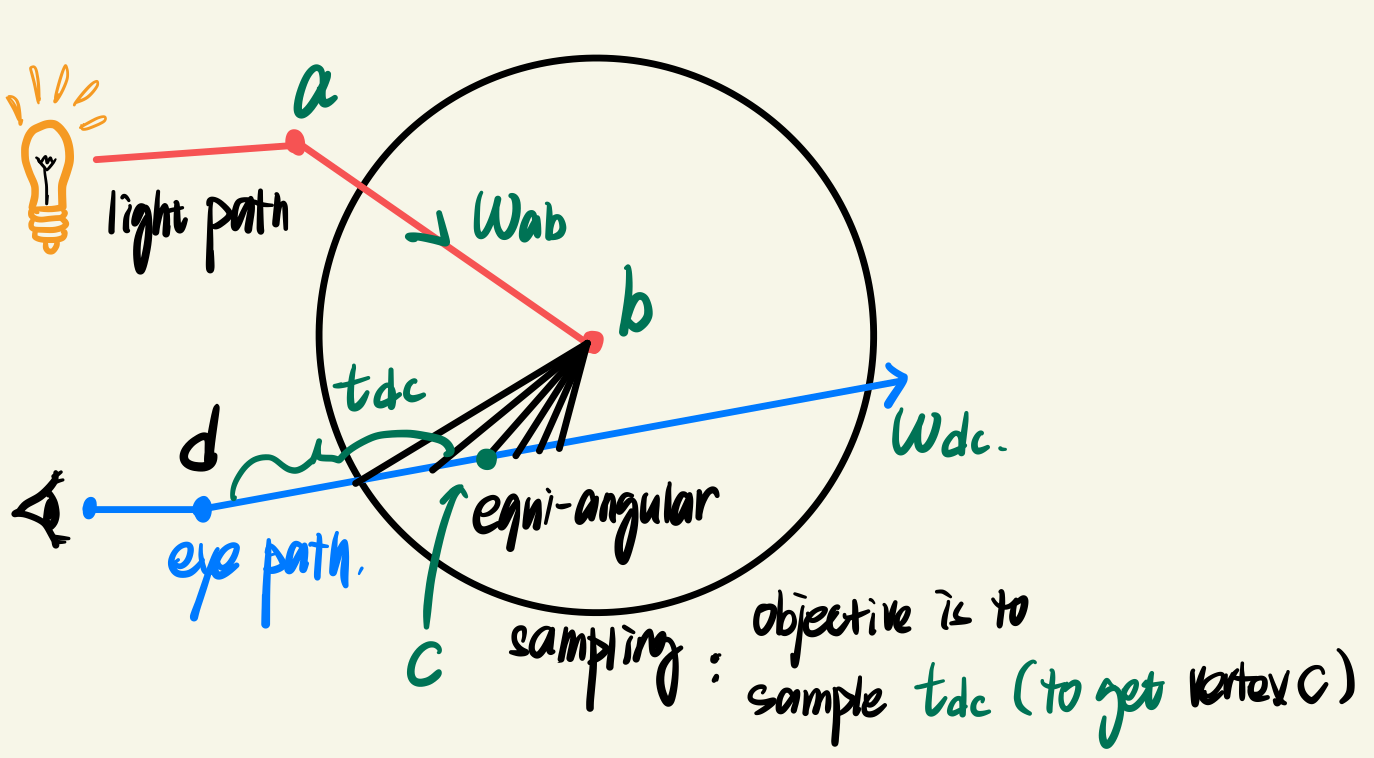
所以为什么，采样的条件分布需要如公式 \(\eqref{equi}\) 所示的 bc距离平方反比有关？其中隐含了度量的转换：我们实际在 \(w_{dc}\) 方向的直线上采样【距离】，但条件是 --- 对于 vertex b 而言，采样结果应当在角度上呈均匀分布。【角度（3D）】与距离之间的转换，由 \(G(b, c)\) 承担：距离越远，单位角度对应的线段长度越大，在某段距离微元内采样的概率就小了。由于是3D空间，故遵循平方反比（而非2D空间下的一次反比）。

此论文中还有很多采样条件分布的计算都与度量转换有关。转换成正确的度量，在正确的空间下积分才能得到正确的结果。

2.2.2 RTE

RTE 本身的形式与 LTE很像，但考虑了光路上 radiance的增加（in-scattering & emission）以及衰减（out-scattering & absorption）。由公式 \(\eqref{remain2}\) 定义的传输率（transimittance）将在接下来的叙述中被写为 \(T_r\)。则我们考虑光线穿过表面进入介质时，介质中某一点朝某一方向的入射 radiance:

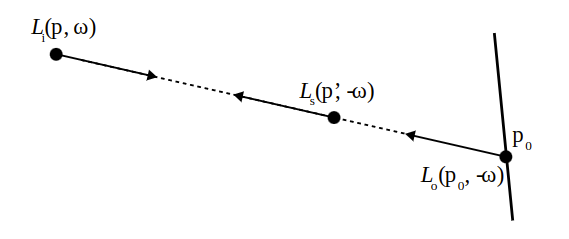
Figure 3. 光线入射介质后的 radiance 计算示意图，图中过p0直线的左侧为介质内部[5]

则，某一点\(p\)的入射 radiance 可以被写为： \[ \begin{equation}\label{rte} L_i(p, w) = T_r(p_0\rightarrow p)L_o(p_0, -w) + \int_d T_r(p'\rightarrow p)L_s(p', -w)dt \end{equation} \] 其中，\(p' =p_0 -tw\)，\(t\) 在\([0, d]\)（\(d\) 为\(p_0\rightarrow p\)的距离）上积分。上式的等号右边有两项：

第一项：代表了外部光线原本传输的部分在传输到 \(p\) 过程中，消耗所剩的部分（\(T_r\) 建模了向外的散射与吸收）
第二项：光线上每一点，都是一个光源（由散射介质会产生内散射的原因决定）。而光源发出的光，自然也需要经过与第一项一样的衰减。此项隐藏了一个积分 - 内散射估计积分：

\[ \begin{equation}\label{in-scat} L_s(p, w) =L_e(p, w) + \sigma_s(p, w) \int_{S^2} f_p(p, w_o, w)L_i(p, -w_o)dw_o \end{equation} \]

其中 \(S^2\) 表示完整球面（介质嘛，就不是半球面了）。故可以看出公式 \(\eqref{rte}\) 包含了所有的 ray-medium interaction 操作。不过一般来说我们不考虑 emission（会发光的烟雾很炫啊）。

emmm，也没什么神秘的对不对？重点不在于理论，在于实现：公式 \(\eqref{rte}\) 存在两个积分，则需要两次采样。我们将公式 \(\eqref{rte}\) 重写为没有 emission 项的二重积分形式： \[ \begin{equation}\label{rte2} L_i(p, w) = \int_d \int_{S^2} T_r(p'\rightarrow p) \sigma_s(p, w) f_p(p, w_o, w)L_i(p, -w_o)dw_odt \end{equation} \] 写为 Monte Carlo 积分的形式，并假设 \(\sigma_s\) homogeneous： \[ \begin{equation}\label{rte-mc} L_i(p, w) = \frac{\sigma_s}{N}\sum_{i=1}^N \frac{T_r(p_i\rightarrow p)}{\text{pdf}(p_i)} \frac{f_p(p, w_o, w)L_i(p, -w_o)}{\text{pdf}(w_o, w|p_i)} \end{equation} \] 上式的采样过程是存在顺序的：首先需要采样空间中的点（由于 phase function 可能与空间位置有关，并且是否发生体散射而非表面interaction也与采样点的位置有关），采样完空间中的点后再采样方向。整个evaluation结果需要我们使用联合分布，联合分布则可以用条件分布与边缘分布表出，并且注意，在这种简单情况下（homogeneous），\((w_o, w)\) 与 \(p_i\) 是独立的。

2.3 实现流程

PBR book写得太好了，第15章非常清晰。从原始的理论到采样的实现以及算法的全流程，能让人完整地看明白，唯一的遗憾就是缺少一些 volumetric path tracing 的 variance reduction 方法。目前AdaPT 中的vpt分支已经被合并到 master 分支下，虽然有结果但噪声问题还是比较严重。根据[4]，方差大可能是 unidirectional volumetric path tracer 无法避免的问题：

Volumetric path tracing with explicit shadow connections suffer from infinite variance when participating media surrounds light sources.

根据我的实验结果发现，情况好像确实是这样：

Null-surface with shadow connections	Explicit shadow connections & media surrounds emitters

Figure 4. AdaPT的一些渲染结果

可以看到，上图中的右图明显符合论文[4]所说的情况：shadow connections + 光源被介质包裹。所以在20000轮迭代之后（共 trace 50亿条光线，允许的最大depth为25 bounces），仍然存在 shot noises。而左图就是单纯地收敛慢。

虽然上述算法仍然存在收敛性上的问题，但至少在debug后（真有些只有我能写出来的脑瘫bug，让我怀疑我根本不适合写代码）能达到与 mitsuba 类似的输出结果。在实现的过程中也遇到一些问题（感觉卡住的地方），下面简要说一下。

2.3.1 VPT 算法流程

算法的主要逻辑如下，在循环开始后：

根据 throughput 判定是否停止。可用的策略有 RR, max iteration 限制以及 min_contribution 限制
ray intersection -- 计算 first intersection point 以及击中位置的法向量、击中物体的 obj_id
根据法向量与光线的关系，判定当前光线在 free space 中还是物体中：如果在物体中，光线与法向的夹角应当小于90°，否则大于90°
计算当前介质，如果 in_free_space = True，则用 world medium，否则用 obj_id 对应的 BSDF内部的medium
进行自由程采样：
1. 判定当前介质是否为散射介质，如果不是散射介质（或者是非透明的BRDF），直接转到【步骤4】
2. 根据指数分布采样平均自由程 \(t_{\text{mfp}}\):
  1. \(t_{\text{mfp}}\) 与 ray intersection的下一表面距离 \(t_{\max}\) 对比，如果 \(t_{\text{mfp}} < t_{\max}\) 则设置 is_mi (is medium interaction) 为 True，否则为 False
  2. 根据 is_mi 的不同，计算这段距离的 transmittance: 如果是表面 interaction，只需要 \(T_r /{\text{pdf}}\)，否则还需要乘以 \(\sigma_s\)
3. if is_mi == True: 得到介质交互点
  1. 计算直接光照部分：如果光源与interaction 点在同一介质内，只要不遮挡一般没有问题，不在同一介质内则根据BSDF track ray（光线尝试从当前位置出发去击打光源，路径上如果遇到了 null-surface 则继续计算，否则若遇到 non-null surface 则直接丢弃此光线，在 track ray 的过程中需要记录 accumulated transmittance）。直接光照的 contribution 计算结束后，加到当前 radiance 上。
  2. 计算传播，NEE：（主要调用 sample），找到下一次应该传播的方向（phase function采样）以及 throughput。回到步骤1
4. else: 得到表面 interaction点
  1. 如同正常path tracer，shadow connection / emitter evaluation 以及 BSDF 方向采样
5. 在累加到结果 radiance 之前，throughput 首先乘以自由程采样中计算的 transmittance

注意，由于暂时用不到MIS，与 Monte Carlo integration 有关的项都可以先除以对应的PDF后直接输出，不需要单独输出PDF（因为用不上）。故，所有的 transmittance 都需要除以对应的PDF：

自由程采样时，根据采样结果计算路径的 transmittance，需要直接除以PDF，这没有什么好说的，毕竟采样是 Monte Carlo 方法的关键步骤。
track rays 时（用于 direct component evaluation），我们需要计算的PDF是整条路上都不发生介质散射（也即方向改变）的PDF。这是由于，direct component evaluation 的光线起始点、终止点是确定的。对于无介质问题而言，直接判断是否遮挡即可。有介质问题，除了遮挡（non-null surface intersection）之外，还必须使得散射不发生（方向不改变）。不过这种想法是很典型的 particle-based 的想法。

2.3.2 注意

Backward tracing类方法，请按照物理过程发生的方向理解。举个例子，自由程采样的时候，如果按照 \(\text{eye}\rightarrow \text{emitter}\) 的方向理解，会很奇怪。与 path tracing 实现时类似，我们要按 \(\text{emitter}\rightarrow \text{eye}\) 的方向：光入射以后，如何与介质交互，而非我的视线如何在介质中被弯折。后者在计算上并没有那么 intuitive。

一开始我没有按照物理过程的顺序理解，实现过程中浪费了很多时间。大概是因为我太蠢了

Direct component shadow connection 在 volumetric path tracing 中效率很低: 只要遇到 non-null surface 就会丢弃直接 shadow ray。对于内部为散射介质的有表面物体而言（也即，不是烟雾），其内部 radiance 也就只能等 ray 出射后，在无介质空间中计算 direct component 或者击中光源来贡献了。

Taichi 有 bug...，debug时我想跑得快一些，迁移到 windows上时，nested struct 的成员函数死活无法调用。深入底层 python API 后也没找到问题，后面给人提 issue 去了...（确实应该是 python - Taichi 版本兼容性问题）。

III. 值得记录

关于diffusive与density estimation:

Section 16.2.2 will introduce the concept of density estimation, which is used to implement a rendering algorithm known as stochastic progressive photon mapping (SPPM). The underlying density estimation that algorithm uses works well on diffuse surfaces because scattered radiance only depends on the surface position in this case to store a 2D radiance discretization, but for glossy surfaces it becomes preferable to switch to other techniques such as path tracing.

各通道不同如何进行采样: RGB 三通道有不同的 \(\sigma_t\) 如何采样？

However, the attenuation coefficient \(\sigma_t\) in general varies by wavelength. It is not desirable to sample multiple points in the medium, so a uniform sample is first used to select a spectral channel i; the corresponding scalar value \(\sigma_t^i\) is then used to sample a distance along the distribution.

Importance sampling heterogeneous medium (\(\sigma_t\) 并非空间均匀)

The most commonly used method for importance sampling Equation (15.13), is known as ray marching

以下是拓展了解，我们并不需要立即知道（非同质介质本身就比较困难）。对于非同质介质（注意，isotropic / anisotropic 为各向同/异性，homo/hetero 为同质/异质）介质而言，有几种处理办法：

regular tracking: 对于每一个voxel，都进行同质假设，采用homogeneous 介质的方法
ray marching: 细分区间 \([0, t_{\max}]\)。在每个细分的区间上做同质假设，则可以估计整个区间上的 \(\sigma_t\) 近似分布，用逆变换采样可以做到比 regular tracking 更好的采样（但是，是有偏估计，很多时候效果都不好）
delta tracking:

an alternative unbiased approach proposed by Woodcock et al. (1965) that was originally developed to simulate volumetric scattering of neutrons in atomic reactors. This technique is known as delta tracking and is easiest to realize when the attenuation coefficient \(\sigma_t\) is monochromatic.