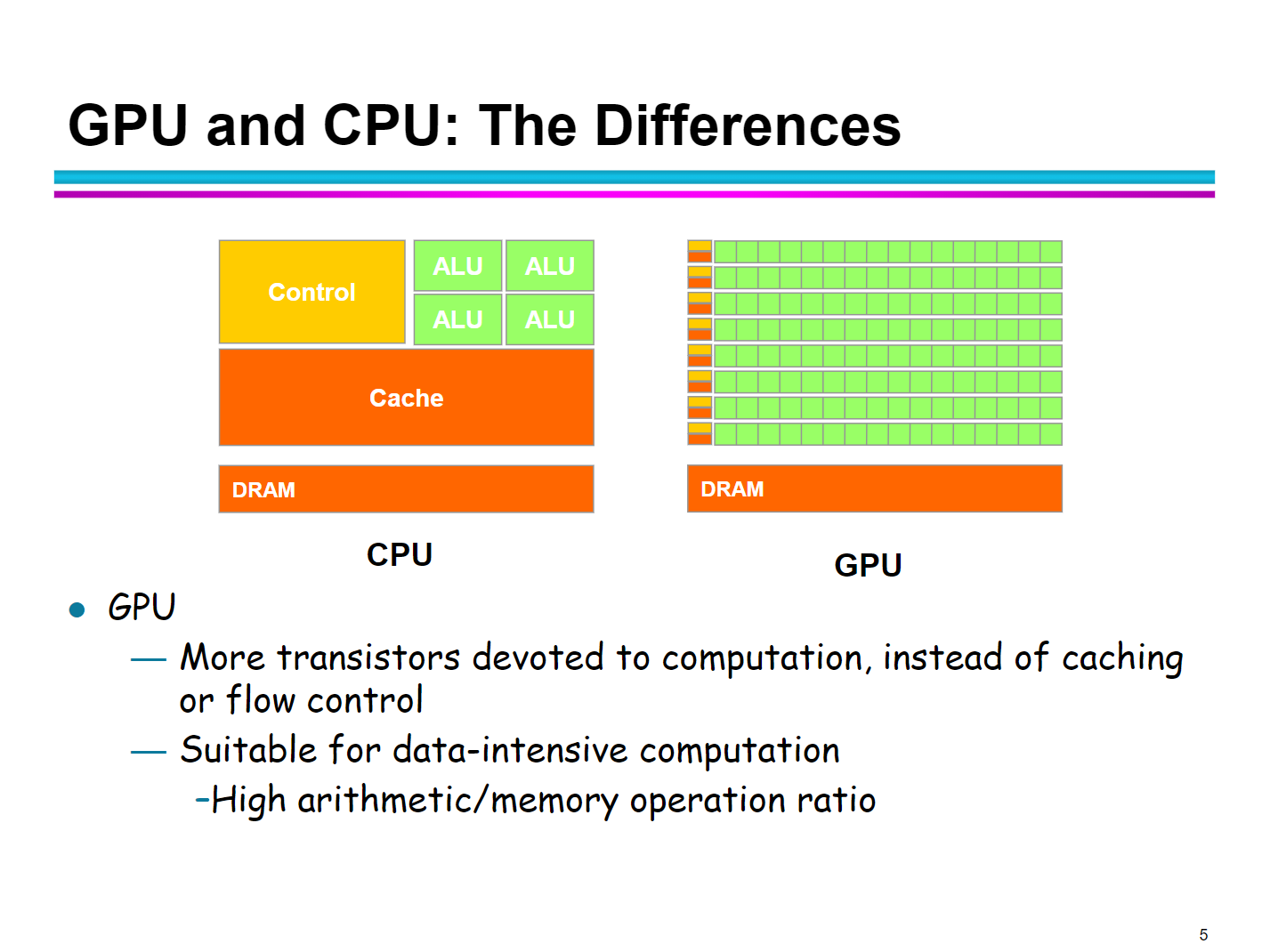
GPU Architecture Intros

Posted on 2021-09-03 Edited on 2021-09-09 In learning Views: Symbols count in article: 6.2k Reading time ≈ 6 mins.

GPU

懂GPU加速必须要懂GPU设计，GPU和CPU太不一样了。之前写CUDA的时候感觉都是瞎写。在开学花个时间补了补，花一天时间（没有实践的那种）看完了加州理工的CS179以及一些附属资料：

Figure 1. 什么？CUDA是Nvidia的？

II. Preliminaries

2.1 名词解释

Vertex 与 Vertex Shader

顶点表示了什么，这很好理解，wikipedia一看就懂：

A vertex (plural vertices) in computer graphics is a data structure that describes certain attributes, like the position of a point in 2D or 3D space, or multiple points on a surface.

但是，vertex从何而来，为什么会有这个数据结构，其存在的意义是什么？这个貌似没有那种一搜就能明白的解释。对于以上的这几个问题，我的理解是：

顶点可以就是模型数据本身，比如模型就给定了一个需要进行渲染的mesh。或者，给定的是一个更加精细的模型，根据某种采样+生成算法，得到的vertex。注意vertex在意义上就有别于point，point是无空间关联关系的，而vertex是存在邻接结构的。

而节点着色器的职责则是：把原本模型空间中的顶点，转换（transform）到屏幕空间坐标下。根据个人的理解，我觉得相机模型就是一个非常简单的顶点着色器，根据外参内参将世界系下的点转换到二维屏幕上。

Primitives 基本图形

GPU渲染管线用于渲染的最基本图形，比如根据顶点着色器的输出，生成很多小的三角形进行后续处理。一般来说，这些primitive都是不可再分的（atomic），这些基本图形之后会被送到。。。比如，光栅化器（rasterizer）中进行一种采样量化操作（因为屏幕的表示能力受到了分辨率的限制）。

Fragment & Rasterizer

Fragment可以认为是每个基本图形量化后的结果，也就是一堆没有着色的像素集合。我们的采样量化精细程度就决定了图像的质量，比如说：当我们需要抗锯齿的时候，可以提高rasterizer的采样精细度，并辅助羽化。光栅化则是我们这段时间接触过的内容，光栅化就是一种采样过程，对于不同精度的数据，将其采样到合适的分辨率下。

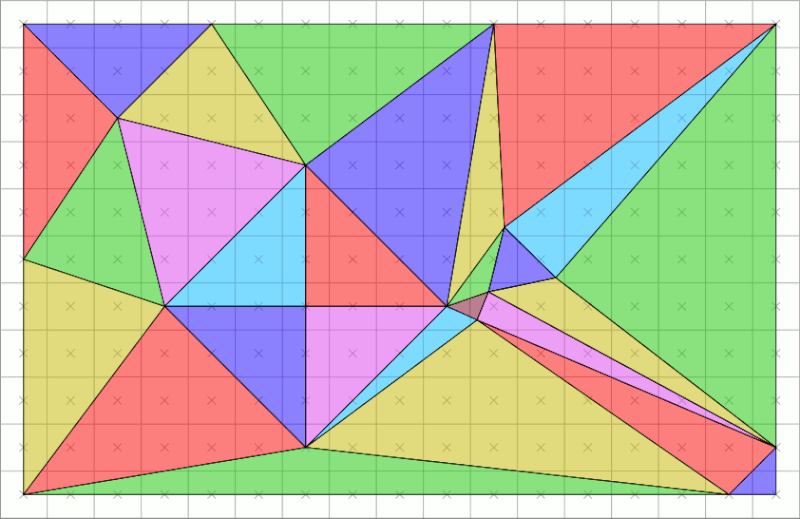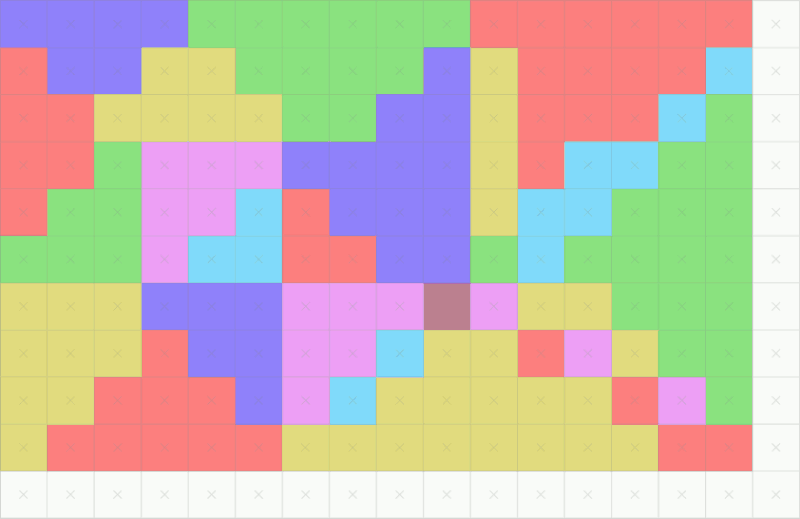
Figure 2. Top-left triangle rasterization rule[1]

在光栅化过程中，经常遇到的问题就是：锯齿。解决锯齿问题就需要一些亚像素精度的操作。

而片段着色器的作用则是：对已经生成的raster图像，进行渲染。比如光照，根据光照模型渲染像素的颜色，或者根据alpha通道信息进行绘制。

2.2 Pipeline & 加速方式

Figure 3. GPU简化管线示意图

从CPU如何到GPU？可能是需要摒弃一些CPU的设计思想的，毕竟CPU/GPU的功能非常不同，自然就应该对应不同的结构，不同的结构就会引出不同的特性。

CPU通常有很多针对一条指令流程优化的方式：

多级cache（prefetching），嵌入式课讲过
分支预测（branch），嵌入式也讲过
乱序执行（这个嵌入式课程中没有显式提到，但是实际上存在于分支处理中，比如将一些指令移动位置以填充分支）

但是这些在GPU中显得不那么重要。GPU的并行任务通常都是：对大量数据做类似的操作，比如Fragment渲染，深度学习。CPU中ALU资源是有限的，每次就只能处理几个输入数据，显然没有办法很好地并行，那么这种需求很可能要求我们需要多个数据处理单元（比如ALU）。如果每个处理单元（比如ALU）都配置多级cache，分支预测等等CPU标配，那么谁来控制芯片的面积？谁来控制不同单元的分支预测？涉及到CPU的一些耗时操作怎么办（比如上下文切换，cache coherence等等）看看：

In computer architecture, a branch predictor is a digital circuit that tries to guess which way a branch (e.g., an if–then–else structure) will go before this is known definitively. --Wikipedia

直接复制CPU cores肯定会让GPU变得笨重。所以这些特性可以都砍掉。

针对我们的第一个要求，显然最好的处理方式是：引入SIMD（single instruction multiple data）的思想。毕竟GPU最常做的事情就是这个，输入不同，操作相同。那么这就涉及到：

多个处理单元fetch/decode/execute同一条指令
多路数据同时输入：取数据不再像CPU处理一样，比如进行像素处理时，一个个位置访问，而是一组组位置访问。有N个处理单元就一次同时访问N个位置，取数据，可以节省大量fetch data的时间。

那么可以认为，CPU是一种标量 (literally) 处理器（这里说的标量和 scalar processor不一样），GPU是一种向量处理器（一次处理一个向量，因为有多个处理单元）。将这些处理单元归为一组，GPU可以有多个这样的组。组间可以遵循流水线设计（避免长时间阻滞带来的吞吐量下降）。

当GPU有多个这样的SIMD核可以并行时，可能可以演化为MIMD。实际上有些架构（比如N卡中），使用的是SIMT（multiple threads），每个线程是独立的，可以存在不同线程不同分支或者是非连续访问的情况。

2.4 更多关键词

参考加州理工CS179 lecture 2 [2]，这里就不赘述了。

III. GPU存储结构

GPU（CUDA为例）的存储结构大致如下：

Figure 4. GPU存储结构

如果要说这几个不同的存储空间的特点，网上应该有很多介绍了。无非就是：

constant/texture是可以由host修改的不可变内存，被cache掉了
global memory是host device可以共同修改的，最慢的内存，shared memory应该多用，因为通常很快，shared memory是同一个block的

之前太年轻，写CUDA程序的时候也没有特别去学过CUDA的内存管理，疯狂使用全局内存，应该是会很慢的吧？global memory倒是没有太多可以说的，接下来主要讲一下shared memory吧。

3.1 Shared memory

shared memory是一种存取很快的内存，硬件实现与L1 cache是一样的（那么可以体会一下其速度级别）。有些地方说，shared memory存取只需要1个周期，有些材料（比如加州理工的PPT）说是5ns（这也很快，毕竟我记得GPU的时钟一般会比CPU慢一些？emmm，说GPU是低频高吞吐率）。

但是shared memory有两个限制：

shared memory物理实现与L1 cache相同，这意味着shared memory不可能太大（SRAM很贵），对于一个block中的warps来说，所有warps使用的共享内存不能超过每个block所具有的内存。这就需要一定的精巧设计：充分利用shared memory使得尽可能多的warps工作。
Bank conflict，这是一个有趣的问题。Bank conflict很像在嵌入式课程中学到的cache冲突问题，cache频繁冲突会引起cache内容的频繁擦写，由于cache coherence，导致多个存储器需要被修改，这很不好。而Bank conflict产生则是引起读写操作的并行化。

Bank conflict的定义：

A bank conflict occurs when 2 threads in a warp access different elements in the same bank. Shared memory is setup as 32 banks

根据stackoverflow上一个佬外“可视化”的bank（或者shared memory分块），加入我们假设管理内存的单元是4字节，那么：

0-3	4-7	...	120-123	124-127
data	data	...	data	data
data	data	...	data	data
...	...	...	...	...

也就是说，这是一个“循环索引”的存储空间。连续的字节流会直接在不同bank之间切换，到末尾bank就会循环切回到第一个bank上。那么，当32个线程（一个warp）所需的内存是线性连续的，那么此时就不会出现两个线程同时访问一个bank的情况。

假设我们的bank设置就是按照如上方式进行的，并且假设线程数量为32。那么当每个线程访问的步长为1是，没有bank conflict。

当步长为2时，显然，只有一半的bank被访问，16个线程之后就会循环回到第一个bank。那么此时会引发两路冲突的bank conflict。

同理，步长为4时，会引发4路冲突...

当步长为32时。有两种说法：

shared memory 也存在broadcast机制，多路访问我直接广播。
32路冲突，这种情况完全串行，需要进行+1步长的padding。

当前的GPU对于bank conflict基本上都更友好，遇到多路同时访问时，可以采用多播(multicast)或者广播策略。这是global memory所没有的。

3.2 Reduction Example: Sum

CS179的lecture 7讲了两个很有意思的例子。第一个就是：并行时我如何对一个数组进行求和？

显然，要利用并行计算的资源，两两求和的过程不能顺序进行（否则就是串行）。显然，求和过程可以分层进行，比如数组长度为32，第一层我就并行执行16个两两相加，保存，同步。第二层就执行8个...

这例子看起来很简单嘛。都能想出来怎么做呢，但实际上这里全是坑。

Figure 5. 直接二分树状分解并行[3]

看起来不错。但是会遇上一个巨大的问题，warp divergence。显然，上图中我们实际使用了16个线程（奇数id线程什么都没做，但是由于处在同一个warp中，还是要执行NOP）。这非常不好，意味着我们每次相加操作之后，还有一段时间的NOP。（很奇怪，为什么可以使用数量为16的warp）

既然这样，那我们可以：

Figure 6. 连续线程并行[3]

虽然我觉得这里有点奇怪，我用了一个大小为8的warp，之后又用了大小为4的warp... 并且bank的组织和我每次使用的warp大小是一致的。

这样确实可以避免warp divergence，但是又会引起新的问题：bank conflict。由于第一次我使用了一个大小为8的block（属实理解不了这个组织，所以我查了一下为什么，列在了3.2末尾），那么bank根据线程数组织：8个bank，啊哦，这就是一个步长为2的2路冲突。因为此时，bank从10这个位置开始，到3，5（5 exactly）位置结束。后面是循环回到第一个bank存储。

第二个循环中，4线程的block是4 banks，那么直接导致了4路冲突... 依此类推。

Figure 7. 序列寻址并行[3]

这样就完全好了。

而关于：“What happens when threads per block is less than 32”问题，我一直觉得这里是存在warp divergence的。来自这个回答 stackoverflow/What will happen if the number of threads in a warp are less than 32?

Regarding warps, it's important to remember that warp and their size is a property of the hardware. Warps are a grouping of hardware threads that execute the same instruction (these days) every cycle. In other words, the size width indicates the SIMD-style execution width, something that the programmer can not change. In CUDA you launch blocks of threads which, when mapped to the hardware, get executed in warp-sized bunches. If you start blocks with thread count that is not divisible by the warp size, the hardware will simply execute the last warp with some of the threads "masked out"

CUDA官方的论坛上，技术大佬貌似没有看懂提问者的问题，提问者想问（就跟我的问题一致）：

I know that you can specify a block size that is less than 32, but I expect that will make part of the warp idle, and reduce resource utilization.

那。。。这些不就是warp divergence吗？除非，GPU做了一些实际的优化，对于一个warp中没有用到的线程直接mask掉，那么第一种实现又有何不可呢？感觉要么就是自己没理解透，再要么就是自己没理解透，最后要么就是这个例子就是有问题，只能强行解释。

3.3 Parallelism Example: Quick sort

这是另一个很有趣的例子：如何在GPU上并行快排？

首先，老师们把这个问题拆解成了两部分。第一部分是：根据条件，选择出符合要求的数组元素形成新的数组。比如：[4, 5, 2, 5, 8, 9, 1, 0, 3, 7] 选出大于4的部分：[5, 5, 8, 9, 7]。

GPU能并行做这个事情吗？回答是可以的，但是不是一步并行的，因为这种往数组中保序添加是不好做的。这样一个任务被拆解为三个串行部分：

True / False 标签：创建一个等大小的flag数组来指示每个元素是否满足要求，满足为1，不满足为0，这个可以全并行。比如例子中[0, 1, 0, 1, 1, 1, 0, 0, 0, 1]
prefix sum，讲flag数组prefix sum求和：[0, 1, 1, 2, 3, 4, 4, 4, 4, 5]，这也是可以并行（分级）的（数组记作prefix）
最后：并行访问flag数组以及prefix sum数组，如果flag[i] = 1，那么原数组[i]保存在新数组的prefix[i]-1位置。也是可以全并行的

这件事做完之后就是标准的快排流程了。选pivot，甚至可以在GPU里递归。